凸函数

article/2025/9/12 2:43:55

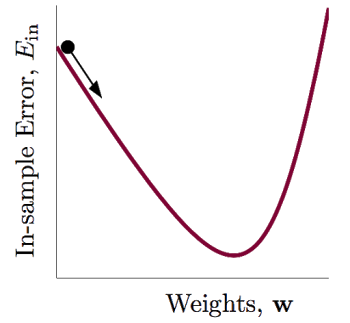
凸函数有一个很好的性质，即只要能证明我们求解的问题是凸函数，最终得到的解一定是全局最优解

首先得注意一下：
中国大陆数学界某些机构关于函数凹凸性定义和国外的定义是相反的。Convex Function在中国大陆某些的数学书中，比如说我上大学那会同济版的高等数学就是指凹函数。Concave Function指凸函数。
如在讲到函数凹凸性的时候，概念是这么给出的：
设f(x)在[a,b]上连续，在（a,b)内具有一阶和二阶导数，那么，
（1）若在（a,b)内f”(x)>0,则f(x)在[a,b]上的图形是凹的；
（2）若在（a,b)内f”(x)<0,则f(x)在[a,b]上的图形是凸的。
个人觉得中国人所说的凸函数可能和凹凸这两个字象形体有关。
关于这一点，我觉得知乎上有些朋友解释的特别好，如
Cave代表洞穴
Concave 凹 Convex 凸

歪果仁是这么认识凹凸函数的
这里写图片描述

怎么样，是不是看到这个，突然就觉得好理解多了呢，我也是从知乎上看到的，狂戳链接
为什么数学概念中，将凸起的函数称为凹函数？

泰勒展开公式

泰勒公式是将一个在x=x_0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，成立下式：

f (x) = f ( x 0 ) 0 ！ + f ' ( x ) 1 ! (x - x 0) + f '' ( x ) 2 ! (x - x 0) 2 + \dots + f ( n ) ( x ) n ! (x - x 0) n

$f(x)=\frac{f(x_0)}{0！}+\frac{{f}'(x)}{1!}(x-x_0)+\frac{{f}''(x)}{2!}(x-x_0)^2+\cdots +\frac{f^{(n)}(x)}{n!}(x-x_0)^n$
当然也可以写成：

f (x) = \sum i = 0 n f ( n ) ( x ) ( x - x 0 ) n n !

$f(x)=\sum_{i=0}^n{\frac{f^{(n)}(x)(x-x_0)^n}{n!}}$
or

f (x) = \sum i = 0 n f (n) (x) * 1 n ! (x - x 0) n

$f(x)=\sum_{i=0}^n{f^{(n)}(x)}*\frac{1}{n!}(x-x_0)^n$

泰勒级数展开(标量)

我们知道，二阶泰勒展开公式为：

f (x k + δ) \approx f (x k) + f' (x k) δ + 1 2 f'' (x k) δ 2

$f(x_k+\delta) \approx f(x_k)+f^{'}{(x_k)} \delta+\frac{1}{2}f^{''}(x_k)\delta^2$
此时，
1.若

f′(xk)=0 $f^{'}(x_k)=0$ ,如果有

f′′(xk)>0 $f^{''}(x_k)>0$ ,则

xk $x_k$ 为局部极小点(反之，局部极大点)，这个在高数书上有，不懂的同学可以回头翻书看看。用几何方法特别好理解，二阶导数大于0说明，一阶导数的曲线呈现严格递增状态，就抛物线而言，斜率代表一阶导数，斜率在逐渐增大，说明抛物线开口向上。
2.如果

f′′(x"k)=0 $f^{''}(x"_k)=0$ ，有可能是一个鞍点，也就是拐点。比如说，

f(x)=x3 $f(x)=x^3$ ,一阶导数和二阶倒数在(0,0)这点处均为0。
总结一下
判断函数极大值以及极小值。
结合一阶、二阶导数可以求函数的极值。当一阶导数等于0，而二阶导数大于0时，为极小值点。当一阶导数等于0，而二阶导数小于0时，为极大值点；当一阶导数和二阶导数都等于0时，为驻点。

凸集(Convex Sets)

定义：一个集合 $C\in\mathbb{R}^N$ 是凸的，则对于任意的 $x_i \in C$ ,有：

θ x 1 + (1 - θ) x 2 \in C

$\theta x_1+(1-\theta )x_2 \in C$

0 \leq θ \leq 1 ， \sum i = 1 n θ i = 1

$0\le \theta \le 1，\sum_{i=1}^{n}\theta_i =1$
简单理解为：
在实数R上（或复数C上）的向量空间中，如果集合S中任两点的连线上的点都在S内，则称集合S为凸集。例如球体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。
如

就不是凸集。

常见的凸集

1.超平面

C = x | a T x = b

$C = {x|a^Tx=b}$
2.半空间
类似于一个分隔超平面将空间切成两半的感觉
这个图来自于七月学习算法

3.多面体
这个应该比较好理解，比如说，三面体，四面体。。。
4.还有类似于平常见到的一些，比如说，圆、椭圆啊，椭球，球体都是凸集
注意：
凸集的交集也是凸集，比如说，圆和椭圆相交，正方体和五面体相交都是凸集。
证明也特别简单：
不妨设两个凸集为P，Q，对于任意两个点x，y∈P∩Q，由于P凸，故线段xy在P中，同理线段xy在Q中，故线段xy在P∩Q中。于是P∩Q凸

凸函数

如果函数f的定义域domf为凸集，且满足
$\forall x,y \in domf,0\le\theta\le1$ 有
$f(\theta x+(1-\theta)y)\le \theta f(x)+(1-\theta)f(y)$ 则称f为定义域上的凸函数

判定方法可利用定义法、已知结论法以及函数的二阶导数
对于实数集上的凸函数，一般的判别方法是求它的二阶导数，如果其二阶导数在区间上非负，就称为凸函数。（向下凸）
如果其二阶导数在区间上恒大于0，就称为严格凸函数。

常见的凸函数

指数函数 $e^{ax}$
幂函数 $x^a,x\in R_+,1 \le a 或者 a \le 0$
负对数函数 - log x
负熵函数 x log x
范数函数 $||x||_p$
$f (x) = m a x (x 1, \dots, x n)$ $f(x)= max(x_1,\dots,x_n)$
$f (x) = x 2 / y, y > 0$ $f(x)=x_2 /y ,y>0$
$f (x) = l o g (e x 1 +, \dots, + e x n)$ $f(x)=log(e^{x_1}+,\dots,+e^{x_n})$