SPSS（八）logistic回归

我们之前的线性回归也好、线性回归衍生方法也好、非线性回归也好，因变量的类型都是连续性的，假如因变量的类型是分类的呢？logistic回归针对的是二分类的因变量

logistic回归

• 基于线性回归模型发展而来

线性回归研究的是连续性因变量与自变量之间的关系

• 有的时候因变量为分类变量，需要研究该分类变量与一组自变量之间的关系

以治疗效果为因变量，结局为治愈/未治愈

如果使用新的宣传方式，决定戒烟的概率是否更高？

 

模型简介

平常的线性回归方程表达式如下

假如我们也是用这种来预测发生概率，则其表达式为

但是在现实情况中，发生率P为因变量，它与自变量之间通常不存在线性关系（一般是两边不敏感，中间敏感，比如收入与轿车拥有率），而且上面表达式不能保证在自变量的各种组合下，因变量的取值仍限制在0~1内，所以数学家们为了解决遇到的这两个问题，将想方设法想找到一种变量变换，能让上式的发生率限制在0~1内，而且两边不敏感，中间敏感，到最后找到了一种变换，将上式的因变量进行如下转换，就能解决我们遇到的问题

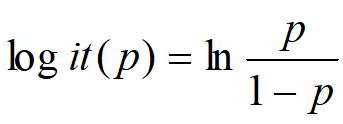
所以上面的表达式可以写成

α是常数项，表示自变量取值全为0时，比数（Y=1与Y=0的概率之比）的自然对数值

Beta为logistic回归系数，表示当其他自变量取值保持不变时，该自变量取值增加一个单位引起比数比（OR）自然对数值的变化量，当概率比较低时候，可以理解概率会上升为原来的几倍

为什么可以直接挂等号呢？当p取0时，趋于负无穷，p取1/2时为0，p取1时趋于正无穷，等式两边值域取值相等

当是上面这个公式和我们平常做回归有什么区别呢？

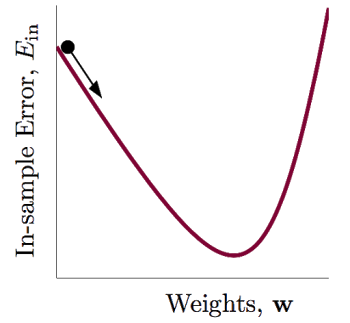
由于因变量为二分类，所以误差项服从二项分布，而不是正态分布，因此，常用的最小二乘法也不再适用，要用迭代方法估计

 

模型用途

 

案例：低出生体重儿影响因素

 Hosmer和Lemeshow于1989年研究了低出生体重婴儿的影响因素

• 影响因素分析，求出哪些自变量对因变量发生概率有影响。并计算各自变量对因变量的比数比
• 作为判别分析方法，来估计各种自变量组合条件下因变量各类别的发生概率，从而对结局进行预测。该模型在结果上等价于判别分析

结果变量为是否娩出低出生体重儿(变量名为LOW，1，低出生体重，即婴儿出生体重<2500克、0，非低出生体重)

考虑的影响(自变量)有：

• 产妇妊娠前体重(lwt，磅)
• 产妇年龄(age，岁)
• 产妇在妊娠期间是否吸烟(smoke，0=未吸、1=吸烟)
• 本次妊娠前早产次数(ptl，次)
• 是否患有高血压(ht，0=未患、1=患病)
• 子宫对按摩、催产素等刺激引起收缩的应激性(ui，0=无、1=有)
• 妊娠前三个月社区医生随访次数(ftv，次)
• 种族(race，1=白人、2=黑人、3=其他民族)

 

(假如只研究是否吸烟对体重的影响，我们可以使用卡方检验，但是目前自变量这么多，卡方检验无能为力)

我们先来看一下卡方检验

从检验结果来看，显著性检验小于0.05，产妇在妊娠期间是否吸烟对低出生体重儿还是有影响的

 

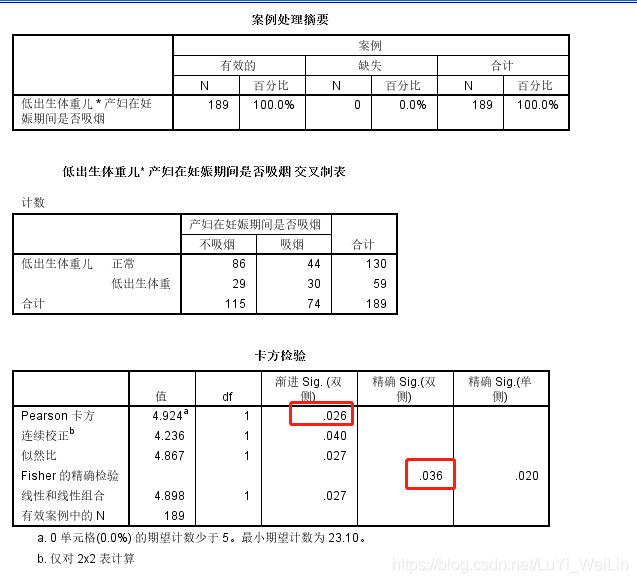
下面我们使用Logistic回归方法

数据集如下

85	0	19	182	2	0	0	0	1	0	2523
86	0	33	155	3	0	0	0	0	3	2551
87	0	20	105	1	1	0	0	0	1	2557
88	0	21	108	1	1	0	0	1	2	2594
89	0	18	107	1	1	0	0	1	0	2600
91	0	21	124	3	0	0	0	0	0	2622
92	0	22	118	1	0	0	0	0	1	2637
93	0	17	103	3	0	0	0	0	1	2637
94	0	29	123	1	1	0	0	0	1	2663
95	0	26	113	1	1	0	0	0	0	2665
96	0	19	95	3	0	0	0	0	0	2722
97	0	19	150	3	0	0	0	0	1	2733
98	0	22	95	3	0	0	1	0	0	2750
99	0	30	107	3	0	1	0	1	2	2750
100	0	18	100	1	1	0	0	0	0	2769
101	0	18	100	1	1	0	0	0	0	2769
102	0	15	98	2	0	0	0	0	0	2778
103	0	25	118	1	1	0	0	0	3	2782
104	0	20	120	3	0	0	0	1	0	2807
105	0	28	120	1	1	0	0	0	1	2821
106	0	32	121	3	0	0	0	0	2	2835
107	0	31	100	1	0	0	0	1	3	2835
108	0	36	202	1	0	0	0	0	1	2836
109	0	28	120	3	0	0	0	0	0	2863
111	0	25	120	3	0	0	0	1	2	2877
112	0	28	167	1	0	0	0	0	0	2877
113	0	17	122	1	1	0	0	0	0	2906
114	0	29	150	1	0	0	0	0	2	2920
115	0	26	168	2	1	0	0	0	0	2920
116	0	17	113	2	0	0	0	0	1	2920
117	0	17	113	2	0	0	0	0	1	2920
118	0	24	90	1	1	1	0	0	1	2948
119	0	35	121	2	1	1	0	0	1	2948
120	0	25	155	1	0	0	0	0	1	2977
121	0	25	125	2	0	0	0	0	0	2977
123	0	29	140	1	1	0	0	0	2	2977
124	0	19	138	1	1	0	0	0	2	2977
125	0	27	124	1	1	0	0	0	0	2992
126	0	31	215	1	1	0	0	0	2	3005
127	0	33	109	1	1	0	0	0	1	3033
128	0	21	185	2	1	0	0	0	2	3042
129	0	19	189	1	0	0	0	0	2	3062
130	0	23	130	2	0	0	0	0	1	3062
131	0	21	160	1	0	0	0	0	0	3062
132	0	18	90	1	1	0	0	1	0	3076
133	0	18	90	1	1	0	0	1	0	3076
134	0	32	132	1	0	0	0	0	4	3080
135	0	19	132	3	0	0	0	0	0	3090
136	0	24	115	1	0	0	0	0	2	3090
137	0	22	85	3	1	0	0	0	0	3090
138	0	22	120	1	0	0	1	0	1	3100
139	0	23	128	3	0	0	0	0	0	3104
140	0	22	130	1	1	0	0	0	0	3132
141	0	30	95	1	1	0	0	0	2	3147
142	0	19	115	3	0	0	0	0	0	3175
143	0	16	110	3	0	0	0	0	0	3175
144	0	21	110	3	1	0	0	1	0	3203
145	0	30	153	3	0	0	0	0	0	3203
146	0	20	103	3	0	0	0	0	0	3203
147	0	17	119	3	0	0	0	0	0	3225
148	0	17	119	3	0	0	0	0	0	3225
149	0	23	119	3	0	0	0	0	2	3232
150	0	24	110	3	0	0	0	0	0	3232
151	0	28	140	1	0	0	0	0	0	3234
154	0	26	133	3	1	2	0	0	0	3260
155	0	20	169	3	0	1	0	1	1	3274
156	0	24	115	3	0	0	0	0	2	3274
159	0	28	250	3	1	0	0	0	6	3303
160	0	20	141	1	0	2	0	1	1	3317
161	0	22	158	2	0	1	0	0	2	3317
162	0	22	112	1	1	2	0	0	0	3317
163	0	31	150	3	1	0	0	0	2	3321
164	0	23	115	3	1	0	0	0	1	3331
166	0	16	112	2	0	0	0	0	0	3374
167	0	16	135	1	1	0	0	0	0	3374
168	0	18	229	2	0	0	0	0	0	3402
169	0	25	140	1	0	0	0	0	1	3416
170	0	32	134	1	1	1	0	0	4	3430
172	0	20	121	2	1	0	0	0	0	3444
173	0	23	190	1	0	0	0	0	0	3459
174	0	22	131	1	0	0	0	0	1	3460
175	0	32	170	1	0	0	0	0	0	3473
176	0	30	110	3	0	0	0	0	0	3475
177	0	20	127	3	0	0	0	0	0	3487
179	0	23	123	3	0	0	0	0	0	3544
180	0	17	120	3	1	0	0	0	0	3572
181	0	19	105	3	0	0	0	0	0	3572
182	0	23	130	1	0	0	0	0	0	3586
183	0	36	175	1	0	0	0	0	0	3600
184	0	22	125	1	0	0	0	0	1	3614
185	0	24	133	1	0	0	0	0	0	3614
186	0	21	134	3	0	0	0	0	2	3629
187	0	19	235	1	1	0	1	0	0	3629
188	0	25	95	1	1	3	0	1	0	3637
189	0	16	135	1	1	0	0	0	0	3643
190	0	29	135	1	0	0	0	0	1	3651
191	0	29	154	1	0	0	0	0	1	3651
192	0	19	147	1	1	0	0	0	0	3651
193	0	19	147	1	1	0	0	0	0	3651
195	0	30	137	1	0	0	0	0	1	3699
196	0	24	110	1	0	0	0	0	1	3728
197	0	19	184	1	1	0	1	0	0	3756
199	0	24	110	3	0	1	0	0	0	3770
200	0	23	110	1	0	0	0	0	1	3770
201	0	20	120	3	0	0	0	0	0	3770
202	0	25	241	2	0	0	1	0	0	3700
203	0	30	112	1	0	0	0	0	1	3799
204	0	22	169	1	0	0	0	0	0	3827
205	0	18	120	1	1	0	0	0	2	3860
206	0	16	170	2	0	0	0	0	4	3860
207	0	32	186	1	0	0	0	0	2	3860
208	0	18	120	3	0	0	0	0	1	3884
209	0	29	130	1	1	0	0	0	2	3884
210	0	33	117	1	0	0	0	1	1	3912
211	0	20	170	1	1	0	0	0	0	3940
212	0	28	134	3	0	0	0	0	1	3941
213	0	14	135	1	0	0	0	0	0	3941
214	0	28	130	3	0	0	0	0	0	3969
215	0	25	120	1	0	0	0	0	2	3983
216	0	16	95	3	0	0	0	0	1	3997
217	0	20	158	1	0	0	0	0	1	3997
218	0	26	160	3	0	0	0	0	0	4054
219	0	21	115	1	0	0	0	0	1	4054
220	0	22	129	1	0	0	0	0	0	4111
221	0	25	130	1	0	0	0	0	2	4153
222	0	31	120	1	0	0	0	0	2	4167
223	0	35	170	1	0	1	0	0	1	4174
224	0	19	120	1	1	0	0	0	0	4238
225	0	24	116	1	0	0	0	0	1	4593
226	0	45	123	1	0	0	0	0	1	4990
4	1	28	120	3	1	1	0	1	0	709
10	1	29	130	1	0	0	0	1	2	1021
11	1	34	187	2	1	0	1	0	0	1135
13	1	25	105	3	0	1	1	0	0	1330
15	1	25	85	3	0	0	0	1	0	1474
16	1	27	150	3	0	0	0	0	0	1588
17	1	27	150	3	0	0	0	0	0	1588
18	1	24	128	2	0	1	0	0	1	1701
19	1	24	132	3	0	0	1	0	0	1729
20	1	21	165	1	1	0	1	0	1	1790
22	1	32	105	1	1	0	0	0	0	1818
23	1	19	91	1	1	2	0	1	0	1885
24	1	25	115	3	0	0	0	0	0	1893
25	1	16	130	3	0	0	0	0	1	1899
26	1	25	92	1	1	0	0	0	0	1928
27	1	20	150	1	1	0	0	0	2	1928
28	1	21	200	2	0	0	0	1	2	1928
29	1	24	155	1	1	1	0	0	0	1926
30	1	21	103	3	0	0	0	0	0	1970
31	1	20	125	3	0	0	0	1	0	2055
32	1	25	89	3	0	2	0	0	1	2055
33	1	19	102	1	0	0	0	0	2	2082
34	1	19	112	1	1	0	0	1	0	2084
35	1	26	117	1	1	1	0	0	0	2084
36	1	24	138	1	0	0	0	0	0	2100
37	1	17	130	3	1	1	0	1	0	2125
40	1	20	120	2	1	0	0	0	3	2126
42	1	22	130	1	1	1	0	1	1	2187
43	1	27	130	2	0	0	0	1	0	2187
44	1	20	80	3	1	0	0	1	0	2211
45	1	17	110	1	1	0	0	0	0	2225
46	1	25	105	3	0	1	0	0	1	2240
47	1	20	109	3	0	0	0	0	0	2240
49	1	18	148	3	0	0	0	0	0	2282
50	1	18	110	2	1	1	0	0	0	2296
51	1	20	121	1	1	1	0	1	0	2296
52	1	21	100	3	0	1	0	0	4	2301
54	1	26	96	3	0	0	0	0	0	2325
56	1	31	102	1	1	1	0	0	1	2353
57	1	15	110	1	0	0	0	0	0	2353
59	1	23	187	2	1	0	0	0	1	2367
60	1	20	122	2	1	0	0	0	0	2381
61	1	24	105	2	1	0	0	0	0	2381
62	1	15	115	3	0	0	0	1	0	2381
63	1	23	120	3	0	0	0	0	0	2395
65	1	30	142	1	1	1	0	0	0	2410
67	1	22	130	1	1	0	0	0	1	2410
68	1	17	120	1	1	0	0	0	3	2414
69	1	23	110	1	1	1	0	0	0	2424
71	1	17	120	2	0	0	0	0	2	2438
75	1	26	154	3	0	1	1	0	1	2442
76	1	20	105	3	0	0	0	0	3	2450
77	1	26	190	1	1	0	0	0	0	2466
78	1	14	101	3	1	1	0	0	0	2466
79	1	28	95	1	1	0	0	0	2	2466
81	1	14	100	3	0	0	0	0	2	2495
82	1	23	94	3	1	0	0	0	0	2495
83	1	17	142	2	0	0	1	0	0	2495
84	1	21	130	1	1	0	1	0	3	2495

Logistic回归涉及到的检验

• Walds检验（变量筛选）：基于标准误估计值的单变量检验

他没有考虑其他因素的综合作用，当因素间存在共线性时结果不可靠

故在筛选变量时，用Walds法应慎重

• 似然比检验（模型比较）：直接对两个模型进行的比较

当模型较为复杂时，建议使用似然比检验进行变量的筛选工作，以及模型间优劣的比较

两模型-2对数似然值之差即为似然比统计量，自由度亦为两模型参数个数之差

• 比分检验（比分检验）

考虑在已有模型基础上引入新变量之后模型效果是否发生改变

 

建模，分析--回归--二元Logistic （二元代表因变量二分类）

刚才我们说(假如只研究是否吸烟对体重的影响，我们可以使用卡方检验，但是目前自变量这么多，卡方检验无能为力)，我们先看看，逻辑回归只研究是否吸烟对体重的影响

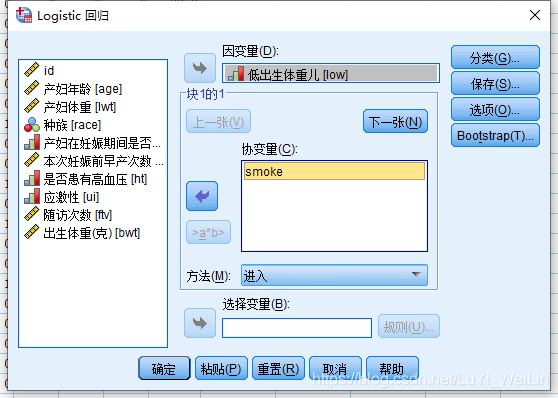
谁是1，就研究自变量对这个变量的影响，反之假如为0的话，得出的结果正负值全反

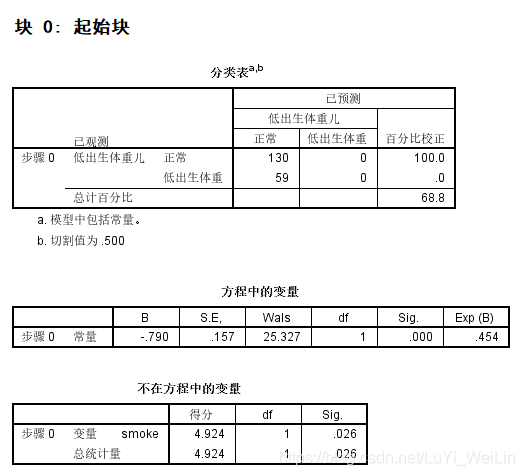
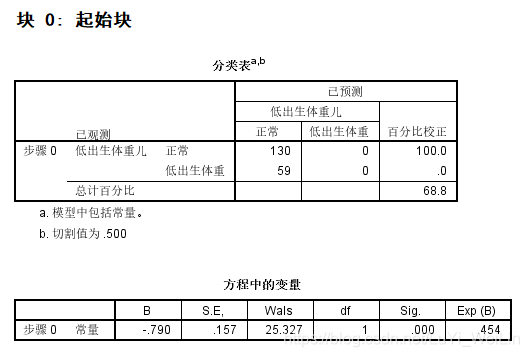
块0：起始块，只有常数项模型，也叫基线模型或无效模型

分类表就是模型预测的情况，下图可以看出划分点为0.5，预测模型全部预测成好人，预测准确率达68.8%，但是这很明显不是我们想要的模型，坏的全部预测成好的了

方程中的变量：Sig.<0.05，证明常数项不为0

不在方程中的变量（比分检验）：把smoke这个变量纳入模型有没有效果，Sig.<0.05,证明纳入进来还是有效果的

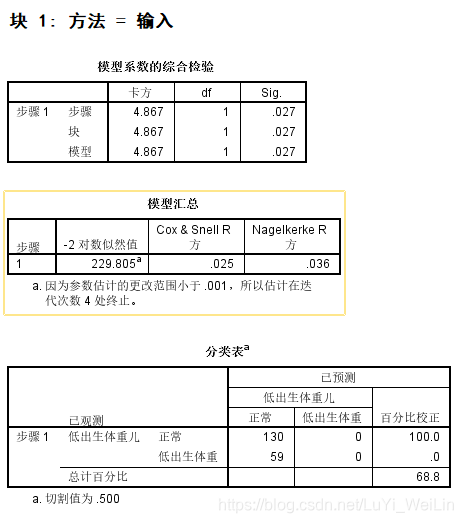
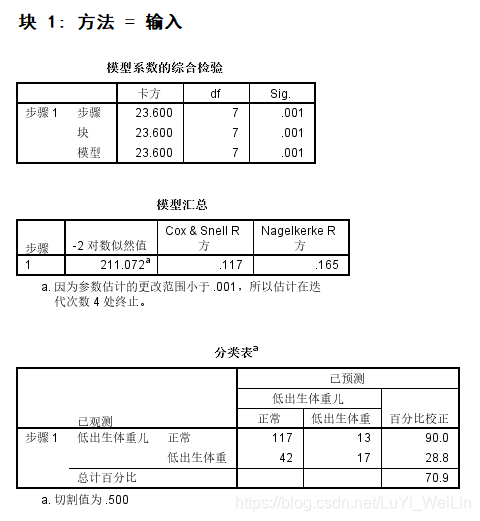
块1：有自变量的模型

模型系数的综合检验：变量的纳入模型与不纳入模型是否有区别，Sig.<0.05,证明有区别，卡方说明变量的加入下降了多少似然比统计量（下面会有介绍到似然比检验）

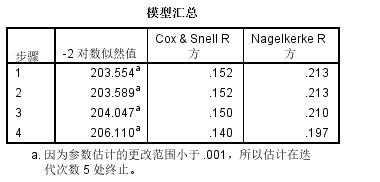
模型汇总（似然比检验）：-2对数似然值衡量的是模型对数据的解释程度，模型的价值指标，越接近0越好，单独看是没有意义的，和其他模型比较才有价值

分类表：查看模型预测结果及切分点

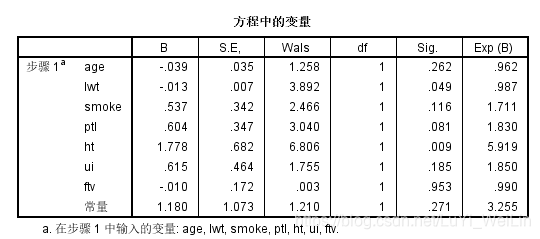
方程中的变量（Walds检验）：Sig.变量纳入模型对模型效果是否显著，Exp（B）称比数比，其他自变量取值保持不变时，该自变量取值增加一个单位引起比数比（OR）自然对数值的变化量，当概率比较低时候，可以理解概率会上升为原来的几倍

 

 

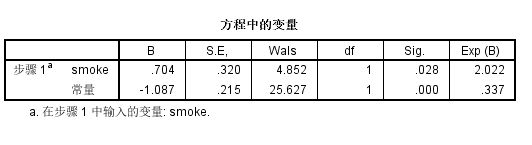
刚才只是考察低出生体重儿与是否吸烟的回归关系，我们现在把所有的二分类自变量和连续类型自变量放进去建模，为什么多分类自变量先不放进去？我们等下再说

分析--回归--二元Logistic

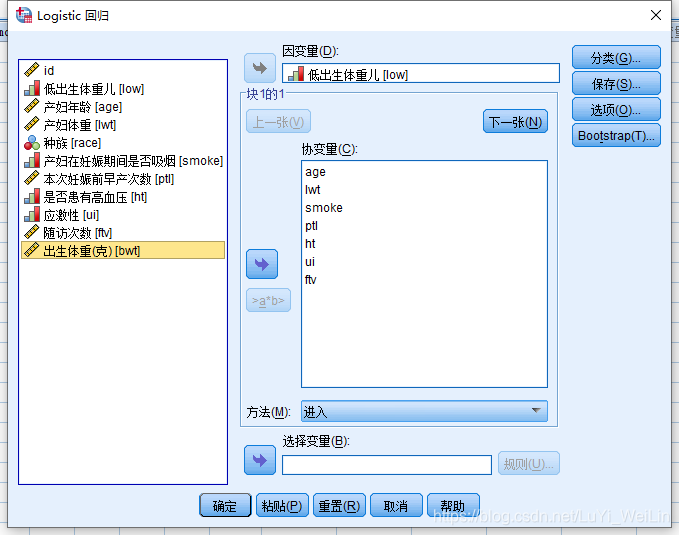
结果解读

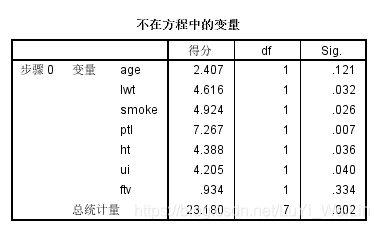
起始块一般没有没有什么变化，但是不在方程中的变量这表格有区别，总统计量显著性<0.05,证明把所有模型都纳入进来有意义，后续再去细看每一个自变量的Sig.进行挑选

块1：

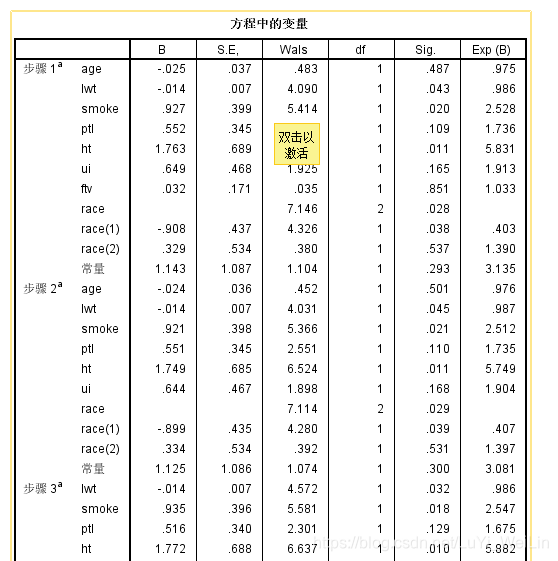
方程中的变量：我们看到有一些变量不显著，Sig.>0.05，直接剔除掉吗？这样做的话存在潜在的危险，因为Walds检验，他没有考虑其他因素的综合作用，当因素间存在共线性时结果不可靠，故在筛选变量时，用Walds法应慎重

我们应该选用比分检验和似然检验来挑选

其他模块的结果解读前面已经讲解

 

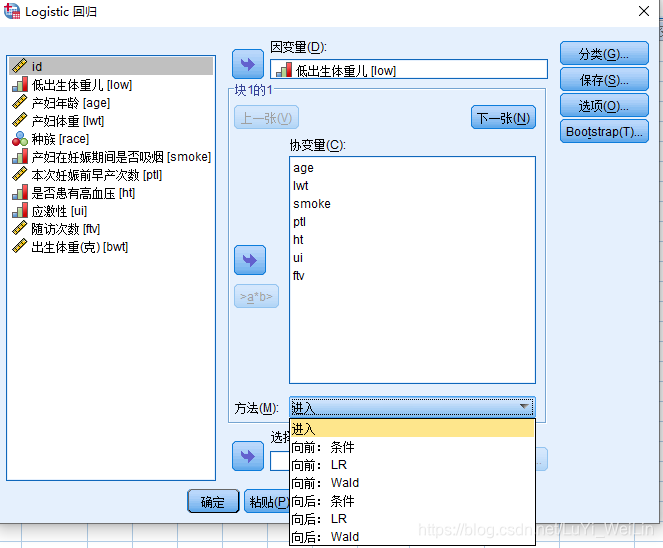
我们知道变量的spss自动挑选有向前法、向后法以及逐步法，当然我们也可以自己手动挑选，毕竟spss自动挑选错误率可达30%

分析--回归--二元Logistic ，我们说过Wald方法不靠谱，最靠谱的方法为LR（似然比检验）或者条件（比分检验），LR（似然比检验）比较好，这里的向前指的是逐步法、向后指的是向后法

我们选择向前：LR

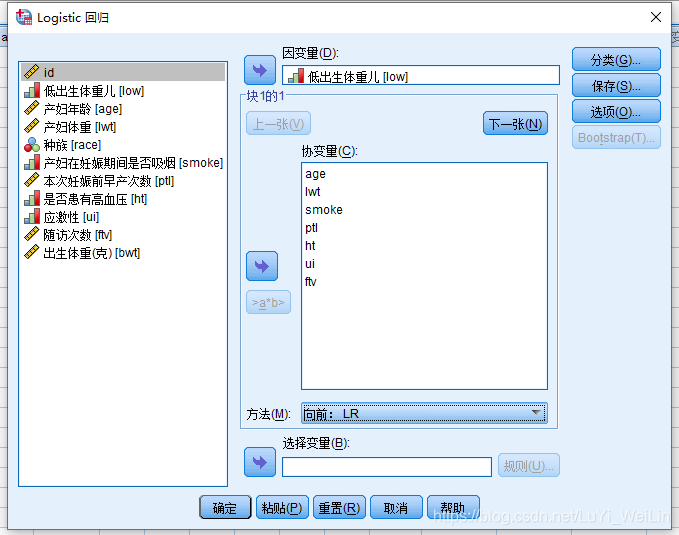
结果如下（块0不截图了，都是一样的）

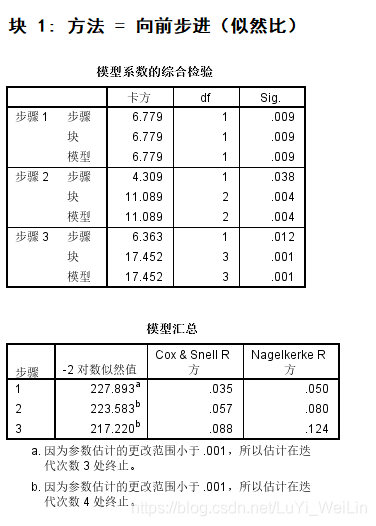
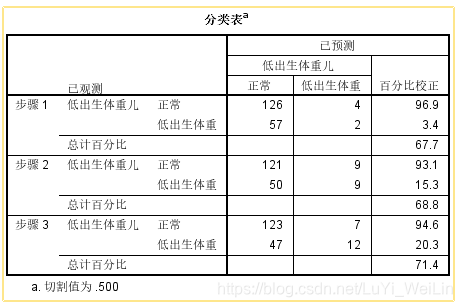
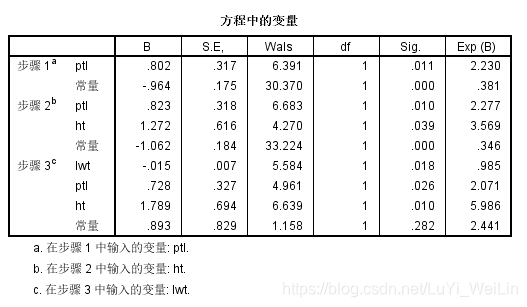
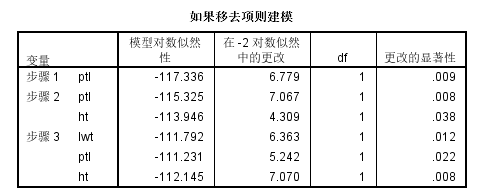
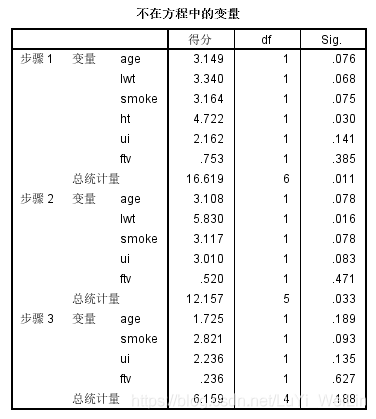
我们看到最终只选择变量lwt、ptl、ht，模型比数比为217.220

 

假如我们使用向后：LR得到结果是什么样的呢？

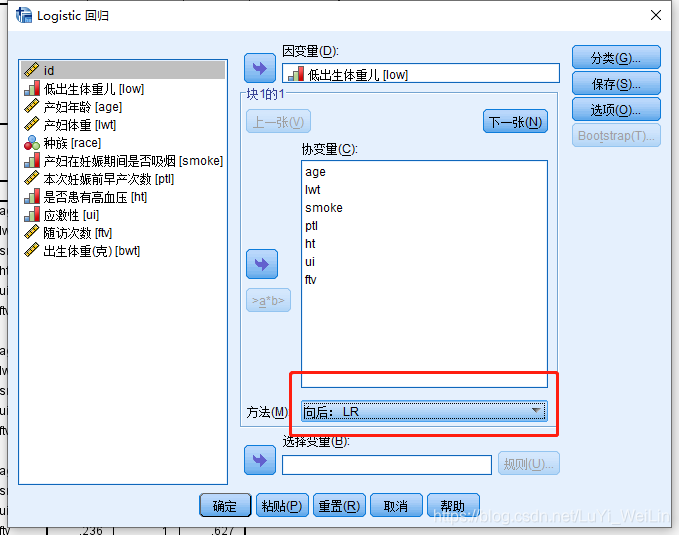
发现其选的变量有四个和向前不一样lwt、smoke、ptl、ht，模型比数比为214.440，遇到这种情况，我们应该多做几次实验或者自己手动挑选变量，假如最后结果还是不一致，用专家经验，smoke其实还是对结果有影响，所以我们选择向后：LR的结果。spss自动挑选的纳入和剔除相对应的Sig.标准是0.05和0.1，可以去调，如下图（选项--步进概率）

 

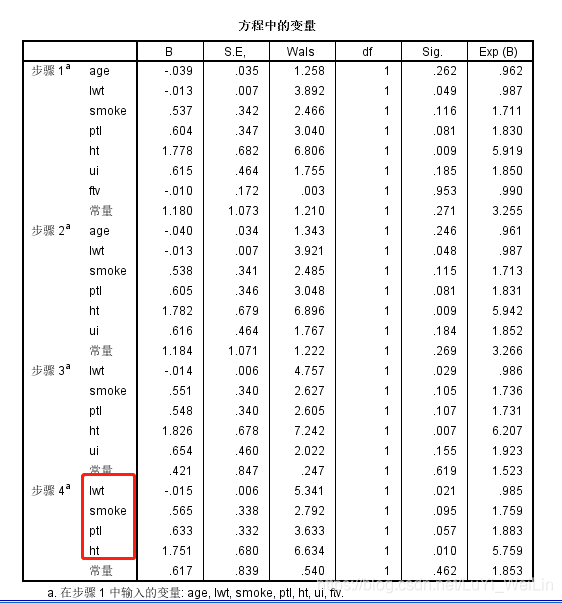
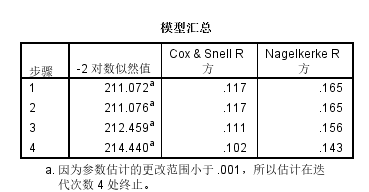
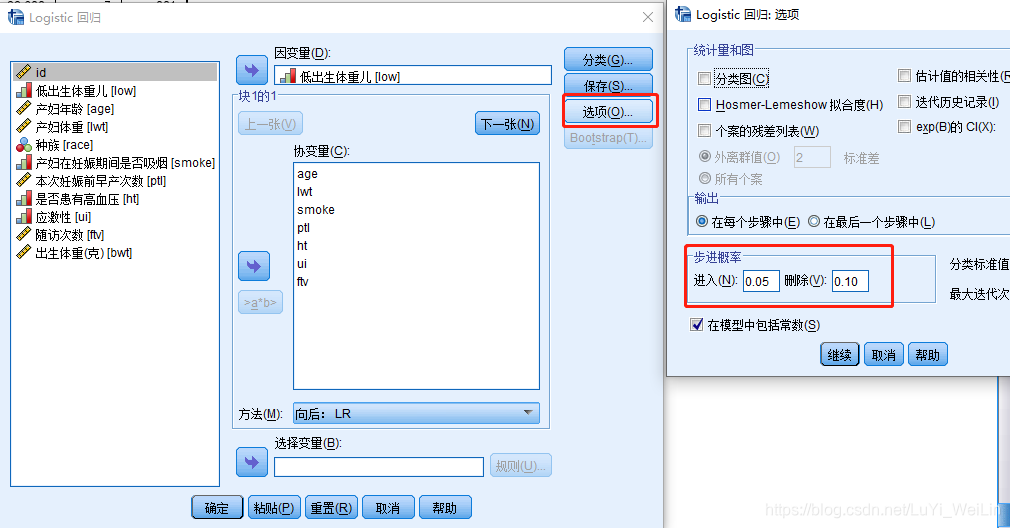
哑变量编码

针对问题：

• 回归系数b表示其它自变量不变，x每改变一个单位时，所预测的y的平均变化量
• 当x为连续性/二分类变量时这样没有问题
• 当x为多分类变量时就不太合适了

无序多分类：民族，各族之间不存在大小问题

有序多分类：家庭收入分为高、中、低三档，它们之间的差距无法准确衡量

强行规定为等距显然可能引入更大的误差

在以上这些情况时，我们就必须将原始的多分类变量转化为数个哑变量（Dummy Variable），每个哑变量只代表某两个级别或若干个级别间的差异，这样得到的回归结果才能有明确而合理的实际意义。

(注意：哑变量必须同进同出，否则含义可能改变)

 

举个例子：

O型是作为对比水平（基础水平），而哑变量V1、V2、V3分别代表了A型、B型、AB型和O型相比的系数

 

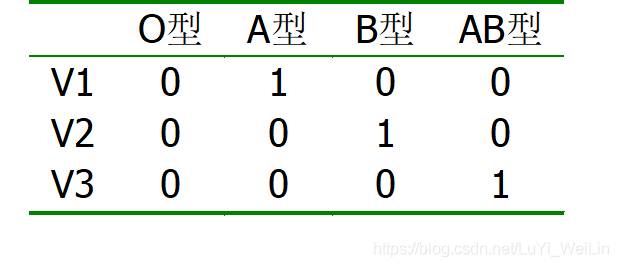
我们的自变量里面有种族，是无须多分类的，所以我们选择其他种族为对比水平（基础水平）

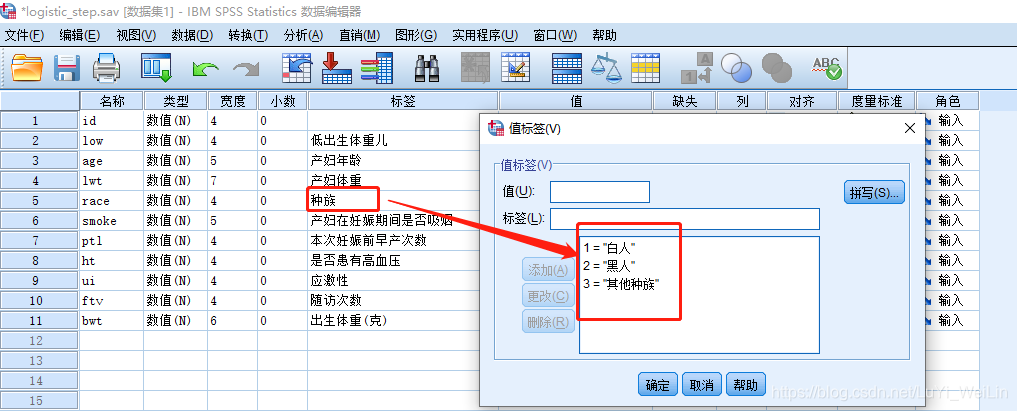
把种族选进来，点击分类，之后设置参考水平即可

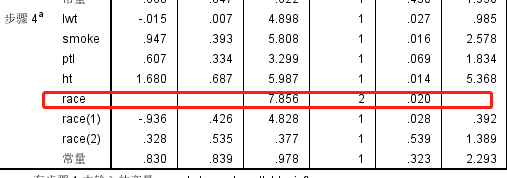
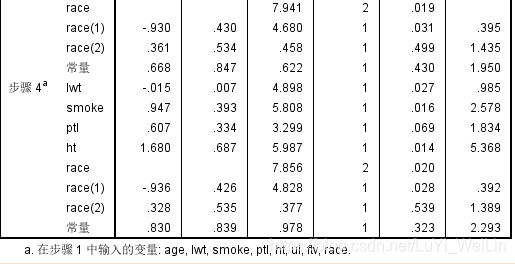
建模结果，模型的似然检验为206.110比之前的模型都要好，其选入的变量有lwt、smoke、ptl、ht、race

注意一下，我们查看哑变量对模型是否有显著性作用先看race总的检验结果为0.02有意义，才去细看里面的race（1）、race（2）

race（1）的比数比Exp（B）为0.392，说明白人相对于其他种族出现低出生体重为0.392倍

   

 

SPSS逻辑回归补充

• 哑变量编码的问题

针对平常的（回归--线性）里面是不支持哑变量编码的，不像Logistic回归这样直接放入协变量点击分类就SPSS自己进行哑变量编码，（回归--线性）里面进行哑变量编码要自己手动动手或者写程序

由于方差分析其实本质上是和（线性--回归）是等价的，假如模型中自变量以分类变量为主的话，放入方差分析的固定因子，自变量会自接变成哑变量的形式

 

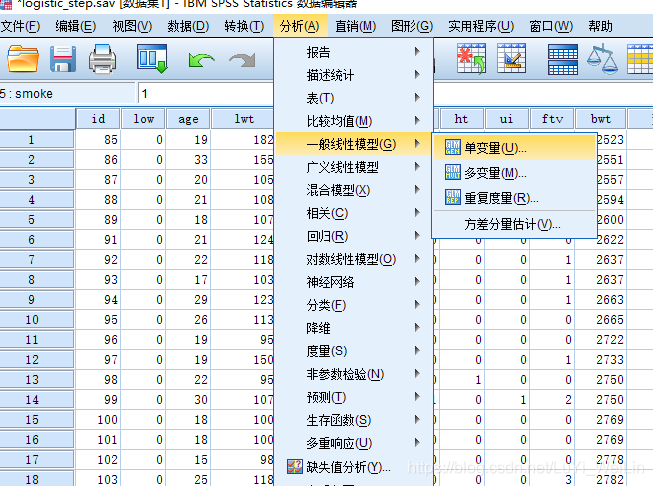
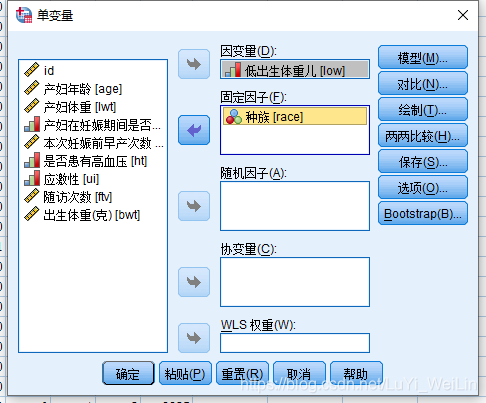
• 交互作用

方差分析里面可以研究交互项对因变量的影响，Logistic回归也是支持的，我们先看看方差分析对应SPPS交互项里面操作

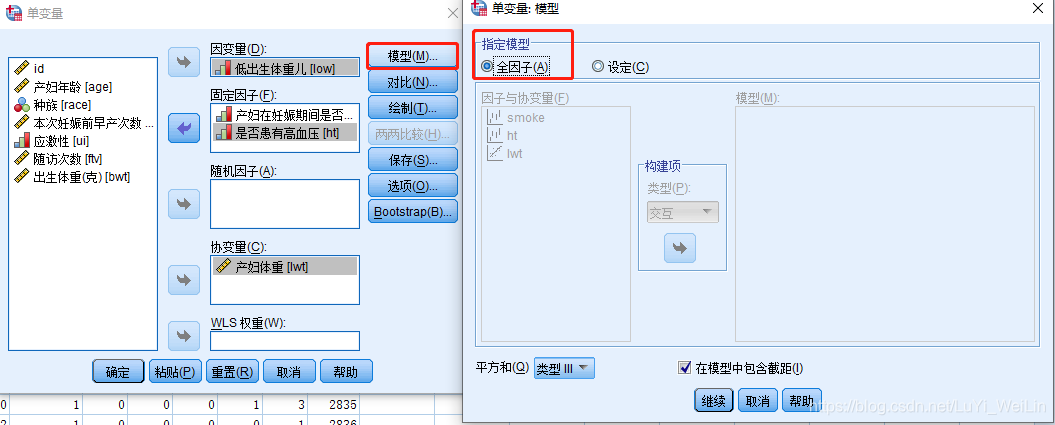
Logistic回归也是支持交互作用的研究的，一次选中多个变量加进去

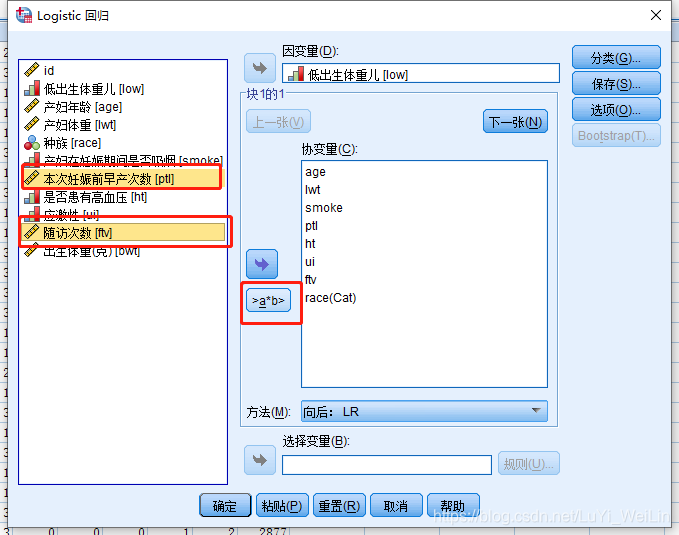
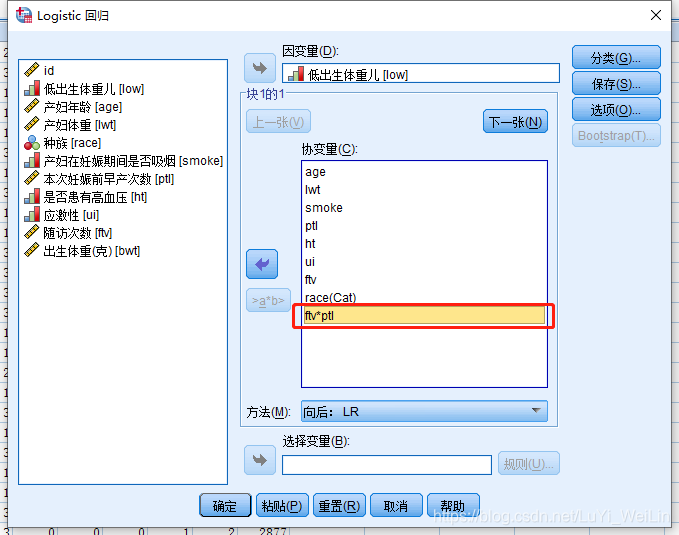
但是（线性--回归）不支持交互作用，假如想研究交互作用，我们可以自己手动做一个新变量，比如a*b作为新的自变量纳入模型，这么麻烦的原因是方差分析已经有这个功能了，方差分析本质上是和线性回归是等价的

 

• SPSS Logistic回归其他好用功能

 

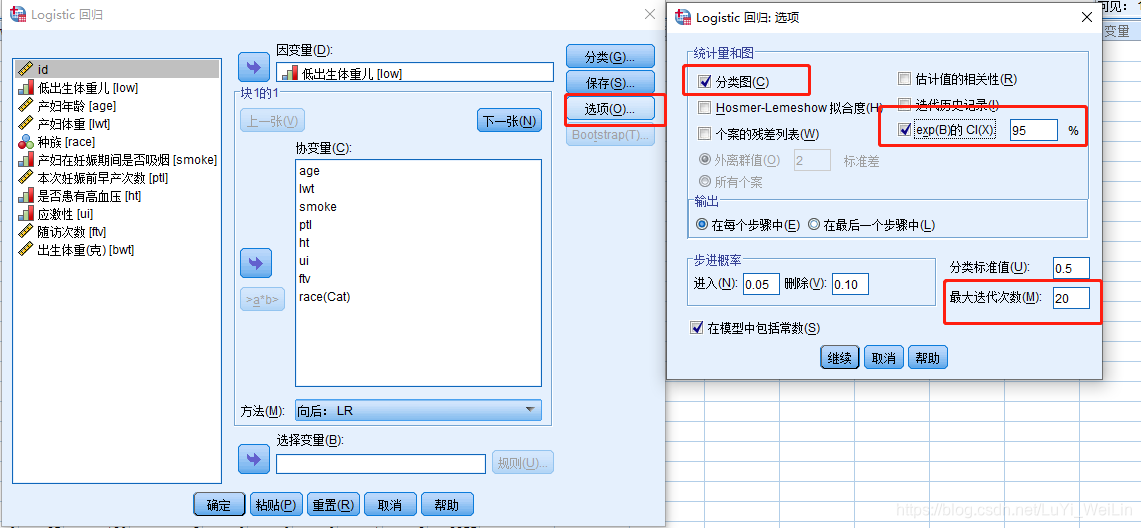
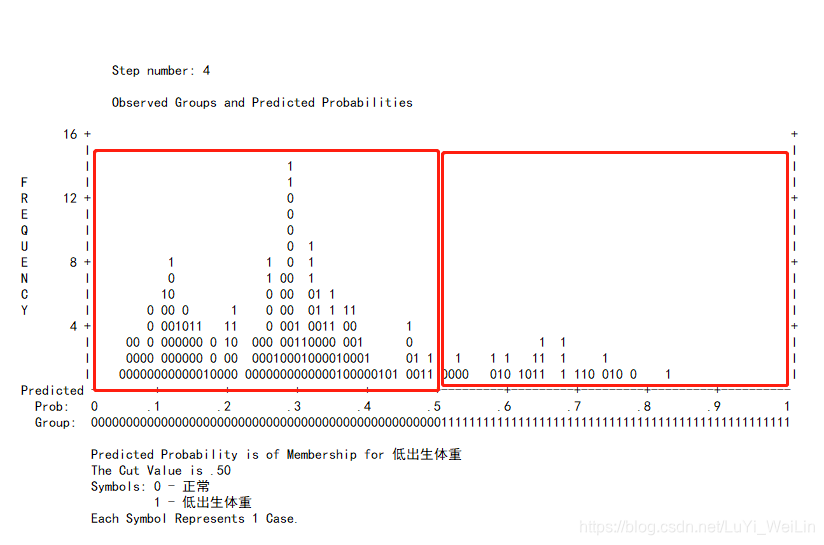
分类图