凸集（Convex sets）

1.仿射集和凸集
仿射集(Affine set)：
定义：如果通过C中任意两个不同点的线位于C中，则集合C⊆Rn就是仿射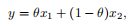
其中，

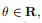
凸集(Convex set)：
定义：如果C中的任意两点之间的线段为C，则集合C是凸的

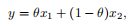
其中，

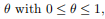
例子：

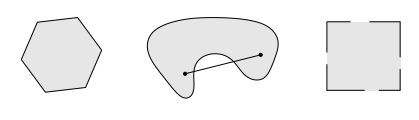
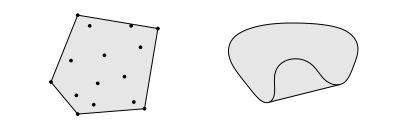
左侧，六边形，包括它的边界（显示较深），是凸的。
中间，肾形集合不是凸的，因为集合中显示的两个点之间的线段不包含在集合中。
右侧，该正方形包含一些边界点，但不包含其他边界点，并且不是凸的。

凸包(convex hulls)
集合C的凸壳，表示 conv C，是C中点的所有凸组合的集合

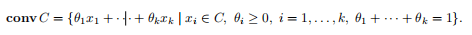
例子：

左侧，一组15个点（显示为点）的凸壳是五角形（显示阴影）
右侧，肾形集合的凸面壳是阴影集。

凸锥(convex Cones)
一个集合C是一个凸锥，如果它既是凸集又是一个锥，这意味着对于任何x1，x2∈C和θ1，θ2≥0，我们有

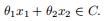
集合C的圆锥壳是C中所有圆锥组合的集合，

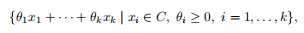
例子：

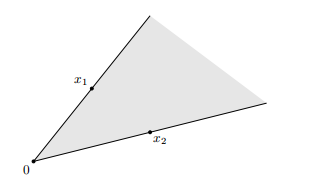
如图所示，饼状切片显示了θ1x1+θ2x2形式的所有点，切片的顶点（对应于θ1=θ2=0）为0；它的边缘（对应于θ1=0或θ2=0）穿过点x1和x2。

如图所示，两个集合的圆锥形外壳（显示阴影）

超平面和半空间(Hyperplanes and halfspaces)

超平面被定义为

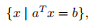
其中a∈Rn、a=0和b∈R。详细来讲，它是x的分量之间的一个非平凡线性方程的解集（因此是一个仿射集）。
如图所示，超平面由一个偏移量x0，加上正交于（法态）向量a的所有向量组成。

一个超平面将Rn划分为两个半空间。
半空间被定义为

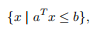
一个（非平凡的）线性不等式的解集。半部空间是凸的，但不是仿射的。
如图所示，由R2中由aTx=b定义的超平面决定了两个半空间。由aTx≥b（非阴影）确定的半空间是沿a方向延伸的半空间。由aTx≤b确定的半空间（显示阴影）沿−a方向延伸。向量a是这个半空间的向外法线。

半空间也可以表示为

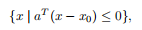
其中x0是相关的超平面上的任意点，即满足aTx0=b。这提出了一个简单的几何解释：半空间由x0加上任何形成钝角（或右向角的向量组成）

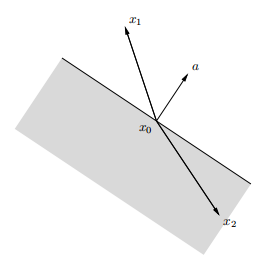
如图所示，阴影集是由aT(x−x0)≤0确定的半空间。向量x1−x0与a形成锐角，所以x1不在半空间中。向量x2−x0与a形成钝角，在半空间中也是如此。

欧几里得球与椭球（Euclidean balls and ellipsoids）
一个欧几里得球（或只是球）被定义为

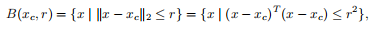
其中，r>0和||·||2表示欧几里得范数，即||u||2=(uTu)1/2。xc是球的中心,r是其半径
B(xc,r)由中心xc距离r内的所有点组成。
欧几里得球的另一个常见的表示法是

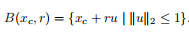
欧几里得球是一个凸集：如果||x1−xc||2≤r、||x2−xc||2≤r和0≤θ≤1，然后

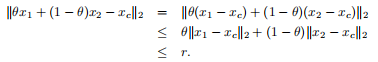
椭球体，它被定为

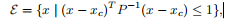
其中，P=PT≻0，P是对称的和正定的。向量xc∈Rn是椭圆体的中心。矩阵P决定了椭球体从xc开始的各个方向延伸的距离；E的半轴的长度由√λi给出，其中λi是P的特征值。
例子

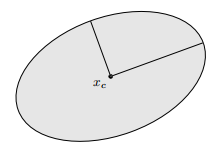
中心xc显示为一个点，而两个半轴显示为线段。
椭球体的另一个常见的表示形式是

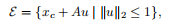
其中，A是正方形的，且为非单数。

范数球和范数锥（Norm balls and norm cones）
范数球，被定义为

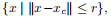
范数锥被定义为

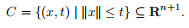
它是（顾名思义）是一个凸锥
如图所示，他是二阶锥，是欧几里得范数的范数锥。

多面体（Polyhedra）
一个多面体被定义为一个有限数量的线性等式和不等式的解集：

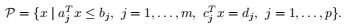
因此，多面体是有限数量的半空间和超平面的交点。仿射集（例如，子空间、超平面、线）、射线、线段和半空间都是多面体。

例子：
如图所示，多面体P（显示阴影）是五个半空间的交点，外正规向量a1……a5.

多面体也可以表示为
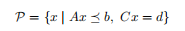
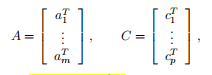u<_v表示ui≤vi,i=1,…,m。

单纯形(Simplexes)
单纯形是多面体的另一个重要的族。被定义为
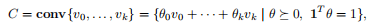其中，1表示包含所有项1的向量。

多面体的凸壳体描述（Convex hull description of polyhedra）
有限集的凸壳，被定义为

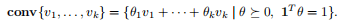
这种凸壳描述的一个推广是

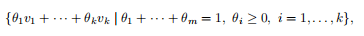
其中，为m≤k。

正半定锥(The positive semidefinite cone)
我们使用符号Sn来表示对称的n×n矩阵的集合，

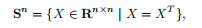
它是一个维数为n(n+1)/2的向量空间。
我们使用符号Sn+来表示对称正半定矩阵的集合：

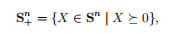
用符号Sn++表示对称正定矩阵集：

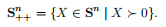
这个符号意味着类似于R+，它表示非负实数，而R++则表示正实数。
如图所示，正半定锥的边界

ok，没了，简单型的看图学知识