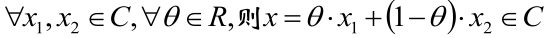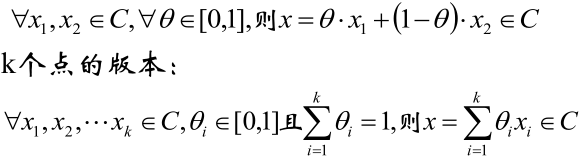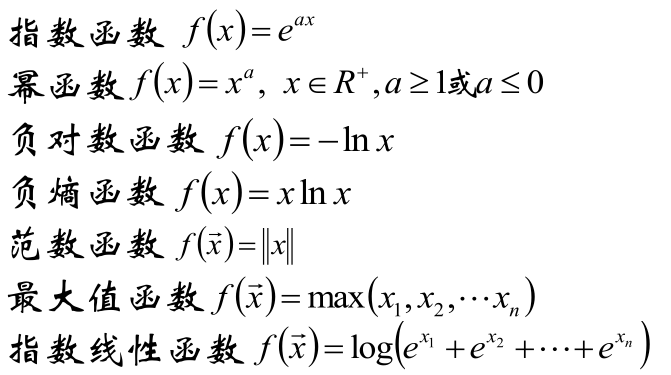本总结是是个人为防止遗忘而作，不得转载和商用。

前提说明：为了方便查阅，我将整个凸优化的内容分成了很多部分，因为后面的部分用到了前面的知识，所以，如果你的目的是查看后面的内容但对前面的某个知识点不甚了解的话可以根据标题查看前面的部分。

凸集

         既然是讲解凸优化，那不了解凸集怎么能行，不过在此之前先了解个和凸集有“一点点”不同的仿射集。

         仿射集：若通过集合C中任意两个不同点的直线仍在集合C内，则称集合C为仿射集。

         数学语言表达的话就是：

                  

         这个知道下就好，下面看看凸集的定义吧。

         凸集：若集合C内任意两点间的线段均在集合C内，则称集合C为凸集。

         定义的数学语言版：

                  

         嘛，定义还是蛮好理解的，我就不多解释了，下面看几个例子来排除下某些容易混淆的家伙。

        

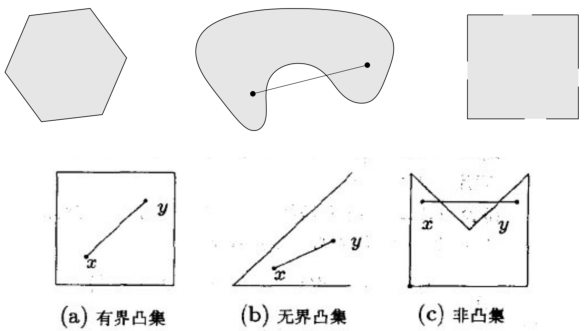
         上图的第一排：

                   第一个：是凸集

                   第二个：不是凸集，原因图中已经标的很清楚了

                   第三个：不是凸集，有些边没有包含集合的话也不能叫凸集。

        

凸集和凸函数：

         有了前面的基础之后，凸函数就好说明了（其实主要是其定义的数学表达公式容易理解）。

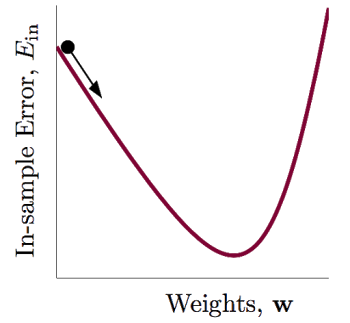
         首先先给出凸函数的图像，如下：

                    

         你可能会问：这不是凹函数吗？

         诚然，在数学中这种图形的函数有的叫凹函数，有的叫下凸函数，反正叫什么的都有，但！在机器学习中，这种就是凸函数，完全没有歧义！

         不过仅仅说“这种是凸函数”还是不能让人信服，于是我们来看看凸函数的定义吧。

         定义：

                  若函数f的定义域domf为凸集，且满足

                        ∀x,y ∈ domf，0≤θ≤1，有

                        f(θx + (1-θ)y) ≤ θf(x) + (1-θ)f(y)     式2

                  则这样的函数f就是凸函数。

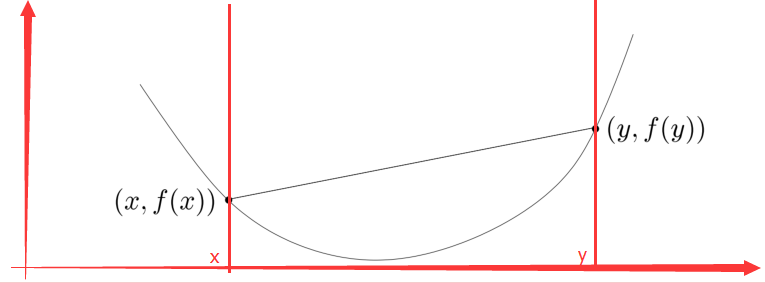
         什么意思？来看下图，下图的弧线是函数f的曲线。

                  

         还记得之前“直线的向量表达”的内容吗？(不记得的话看看本总结的最开始)。

         θx + (1-θ)y：代表x和y之间的某个点，如果θ=0，就是y点，如果θ=1就是x点。

         于是式2的左边不用多说，仅仅是单纯的把(θx + (1-θ)y)这个点带入函数f，也就是上图x和y之间的弧线。

         还是根据“直线的向量表达”的知识，式2的右边就是点(x,f(x))和点(y,f(y))之间的线段。

         于是定义就是表达：如果“函数f上任意两点的连线”在“函数f这两点之间函数f图像”的上面的话，这样的函数就是凸函数。

         或者简单的说：如果悬线在函数上方，那这样的函数就是凸函数。

 

         凸函数的定义OK了，就进一步说点东西：

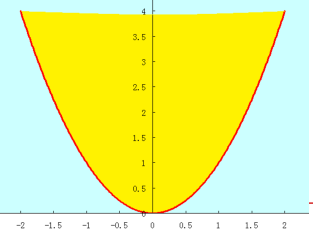
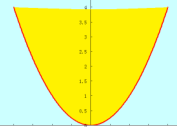
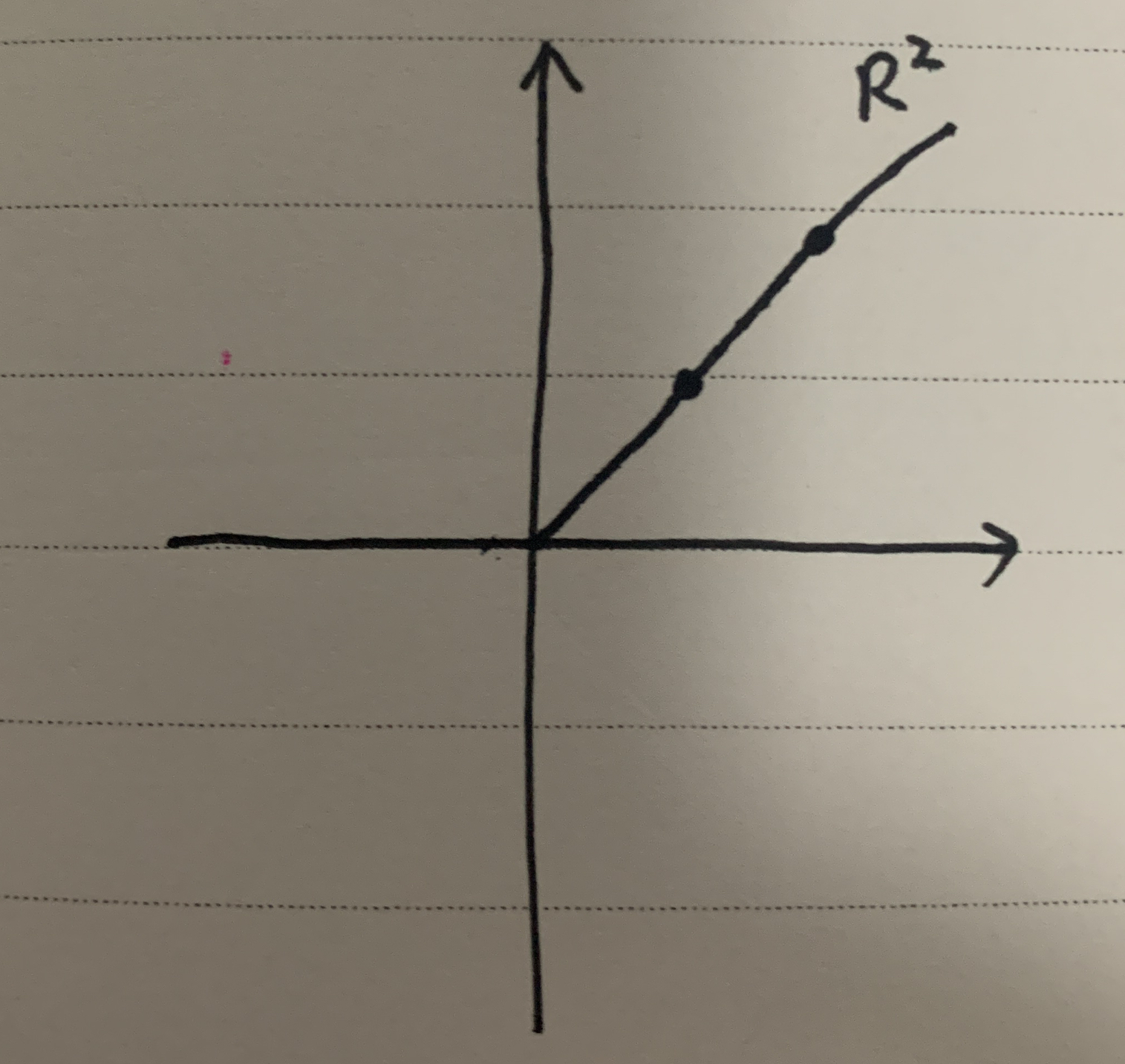
         如果一个函数是凸函数，则该函数的图像上方区域一定是凸集。反过来也成立，即：如果一个函数图像的上方区域是凸集，则该函数是凸函数，于是如下图所示：

                           

         这个图像就是函数y=x²的图像，这个函数是个在明显不过的凸函数，它的上方区域就是凸集。

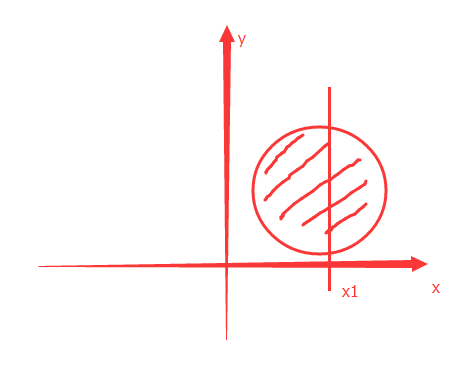
注意：          凸集并不一定都能对应到凸函数，因为函数的最根本条件是：对于函数y=f(x)，只有一个y，而如下图所示                   我取一个点x1，在经过圆构成的凸集时产生了2个y，这与函数的最根本条件就冲突。

         一些比较常见的凸函数有：

                  

 

保持函数凸性的算子

         知道了什么是凸函数后，这里说下什么样的运算会让函数不丢失凸性。

         下面的f(x)代表凸函数，而下面的运算的结果会继续保持凸性：

                  1，凸函数的非负加权和

                            f(x) = w₁f₁(x)+ ... + w_nf_n(x)，w_n > 0

                   2，凸函数与仿射函数的复合

                            g(x)= f(Ax + b)

                            eg：y = u²是凸函数，而u =ax+b，则 y = (ax+b)²也是凸函数

                   3，凸函数的逐点最大值、逐点上确界

                            a，f(x) = max(f₁(x),..., f_n(x))

                            b，f(x) = sup g(x,y)，其中y∈A

         这里特别说明下上面的第三条，一是仅看公式不太好理解，二是这条十分重要！

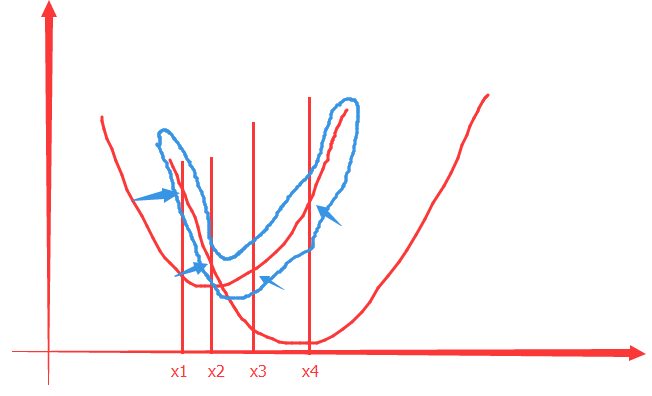
         第三条中的a的意思是：如果fn(x)是凸的，则对fn(x)逐点最大值形成的函数也是凸的，见下图：

                  

         这里我随便给了两个凸函数(两个红色的曲线就是这两个函数的图像)，我在坐标轴上随便取四个点x1,x2,x3,x4，这四个点在两个函数中都有对应的值，而这时我们取较大的那个，即：图中蓝色箭头所指的地方，按照这样的方式把两个函数的定义域取一遍从而形成一个新函数：蓝色弧线框住的部分。而这个新函数也一定是凸函数。

         好了，上面的理解了后我问读这篇文字的你一个问题：直线是凸函数吗？

         答案是：是。

         因为，如下图：

                   图1

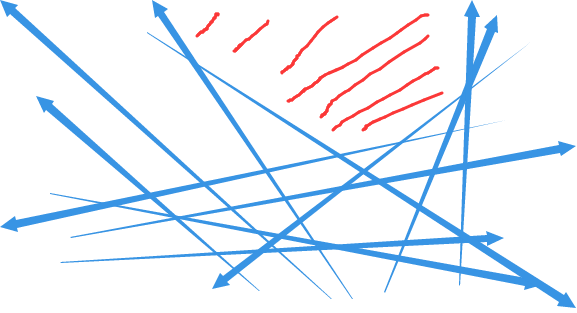
         上图那些蓝色的是直线（不要吐槽箭头，QQ截图里没法画直线....），这些直线够乱的了吧，这时按照上面第三条中的a中的说法，我取所有直线的最上面的区域，即红色那块，是凸函数吧！于是直线就是凸函数。

         顺便一提：上面包围红色的那些线就是这所有直线函数的上确界。

         至于，上面第三条中的b，其实就是a的连续版本，它的意思是：如果g(x, y)是凸的，我们对y在所有的集合中取上界(和max几乎一个意思)，那它的结果f(x)也是凸的。