Logistic模型是经典的用于分类问题的模型，通常用于判断一件事物的好坏或将其分类。本文着重介绍logistic模型的在二分类上的应用，对于数学的推导证明则省略，logistic模型还有很多拓展的使用，如正则化、通过惩罚项调整系数等都值得学习研究，但本文不做赘述只讨论最基本的应用。
本文仅用于个人学习笔记使用
Reference：《从零开始学习python数据分析和挖掘(第二版)》

logistic模型的基本介绍

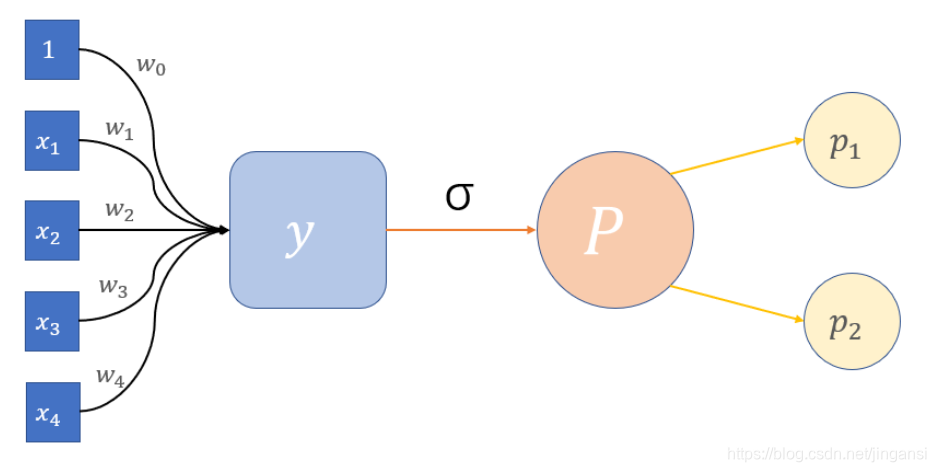
本文研究的问题为二分类问题，一般研究的问题有两类：一是判断问题好与坏的情况；二是将某种物质进行分类。例如医学上，可通过某些体检指标来判断是否确证某种病症。若采用之前的回归模型来描述，将0.5作为阈值——函数值小于0.5则表示未得病；大于0.5则表示得病的话，可能会造成较大的误差。所以通常采用logit函数将函数值压缩到0-1之间，其表达式如下所示：
$$y=\frac{1}{1+e^{-z}}$$
令：$$z={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p$$
则可以得到：$$p=h_{\beta }(x)=\frac{1}{1+e^{-({\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p)}}$$
此处的p表示正向的概率，$h_{\beta }(x)$可称为logistic模型，即为本期文章的重点。继续看下面的公式：
$$\frac{p}{1-p}=e^{{\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p}$$
此时若我们将两边取对数，则可得：
$$log(\frac{p}{1-p})={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_p{x}_p$$
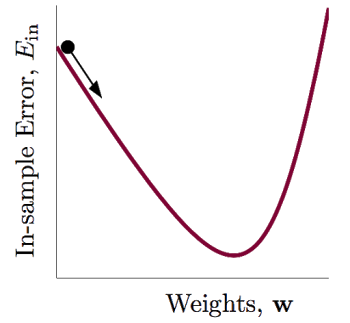
此时又回到了线性回归的模型形式，这很神奇捏。$\frac{p}{1-p}$ 称为发生比，表示发生正向事件的概率占发生反向事件的概率的百分比。logistic模型中的参数$\beta$正是通过这个方程求解出来的，但是如使用一般的OLS算法无法求解，一般采用极大似然估计法以及梯度下降算法迭代进行求解。这个过程我们不做推导，可自行查阅相关文献。

python中实现logistic回归

接下来让我们来看看python是如何实现logistic模型的建立：
数据集：根据6个跟运动状态有关的自变量，三个与方向有关，三个与加速度有关，根据该数据集构建logistic模型用于判断该用户是跑步还是步行。
使用模块：sklearn的子模块：linear_model中的LogisticRegression类。
代码：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn import model_selection sports = pd.read_csv(r'Run or Walk.csv')
predictors = sports.columns[4:]
X = sports[:][predictors] 
y = sports.activity 
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234) 
# 训练模型
sklearn_logistic = linear_model.LogisticRegression().fit(X_train, y_train)
# 返回模型的各个参数
print('logistic模型的β系数：\n',sklearn_logistic.intercept_, sklearn_logistic.coef_)

解析： 读取文件、分割选取自变量和因变量、分割训练集测试集的基本操作不做叙述，重点来看logistic模型的求解：
通过调用LogisticRegression()类中的函数fit()对训练集的因变量和自变量进行训练，得出模型的表达式的参数$\beta$结果如下所示：

logistic模型的β系数：#常系数以及变量前的系数：[4.36637441] [[ 0.48695898  6.87517973 -2.44872468 -0.01385936 -0.16085022  0.13389695]] 

最终可建立模型：
$$h_{\beta }(x)=\frac{1}{1+e^{-(4.37+0.49x_1+6.86x_2-2.45x_3-0.01x_4-0.16x_5+0.13x_6)}}$$
模型系数的意义：
以$x_1$为例，其系数为0.49，表示在其他因素均不变的情况下，$x_1$的数值每增加一个单位，会使得跑步发生比变化0.49倍。
模型的预测：

sklearn_predict = sklearn_logistic.predict(X_test)
res = pd.Series(sklearn_predict).value_counts()
print('预测结果：\n', res) 

输出结果：

预测结果：
0    12119
1    10028
dtype: int64

使用predict()函数进行预测，得到的结果分别显示被判断为了跑步或走路的样本的个数。

模型的评价

混淆矩阵

定义：
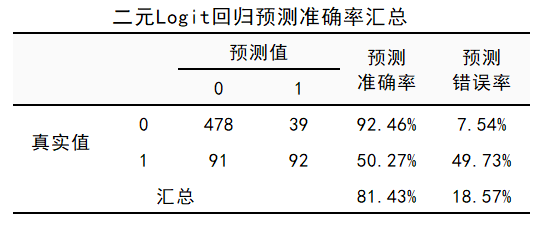
混淆矩阵是2×2的矩阵，其基本形式如下所示。

	实际为0	实际为1
预测为0	A, 预测正确为0	B, 错将1预测为0
预测为1	C, 错将0预测为1	D, 预测正确为1

A可用TN表示，B可用FN表示；C可用FP表示，D可用TP表示。定义了这些数值，我们可以定义如下几个指标：
$$Accuracy=\frac{A+D}{A+B+C+D}，衡量模型对整体数据的预测效果$$
$$Sensitivity=\frac{D}{B+D}，正例覆盖率$$
$$Specificity=\frac{A}{A+C}，反例覆盖率$$
$$Precision=\frac{D}{C+D}，正例命中率$$
代码：

# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0, 1])
print('混淆矩阵：\n', cm)# 混淆矩阵热力图
import seaborn as sns
sns.heatmap(cm, annot=True, fmt = '.2e', cmap = 'GnBu')

输出结果：混淆矩阵的热力图如下所示。该热力图颜色越深的地方其数值越大，且图中对角线上的颜色最深，表明预测正确的占比较大。

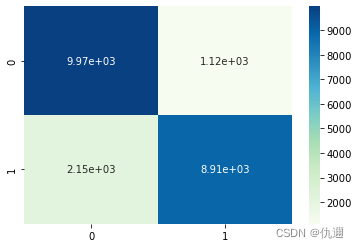
ROC曲线，AUC值

ROC曲线则是通过可视化结果来判断模型的好坏。它的指标有两个：一是x轴的1 - Specificity；二是y轴的Sensitivity。利用python我们可以轻松地绘制出ROC曲线以及其面积AUC数值如下所示：
代码：

# ROC曲线和AUC数值
# y得分为模型预测正例的概率
plt.figure()
y_score = sklearn_logistic.predict_proba(X_test)[:, 1]fpr, tpr, threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr, tpr)import matplotlib.pyplot as plt
#绘制面积图
plt.stackplot(fpr, tpr, colors='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加ROC曲线的轮廓
plt.plot(fpr, tpr, color = 'black', lw = 1)
# 添加对角线
plt.plot([0, 1], [0, 1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5, 0.3, 'ROC curve (area = %0.2f)' % roc_auc)plt.xlabel('1-Specificity')
plt.ylabel('Specificity')plt.show()

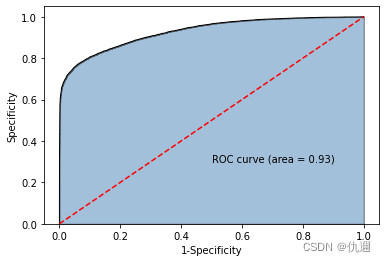
输出结果：该ROC曲线下的面积即为AUC的数值，为0.93。其值越接近1表明该模型的拟合效果越好。

后记
分类模型除logistic模型外，fisher判别分析、SVM支持向量机、决策树等大量的机器学习算法都可解决分类问题。在真实的项目中或数学建模竞赛时，通常是利用python自动化编程的优势，将所有可能用到的模型进行训练、测试，并使用模型评估的方法对该算法下的结果进行评估，最终选择最为优秀的模型进行应用，这也是机器学习算法选择的基本思路。