一句话概括

凸（Convex）：在该区间函数图象上的任意两点所连成的线段上的每一个点都位于函数图象的下方(或上方)。

非凸（Non-Convex）：函数在该区间上有多个极值,即系统有多个稳定的平衡态。

一、凸和非凸的区别

直观判断一个集合是否为Convex的方法，如下图：

若集合中任意两点连线上的点都在集合内，则该集合为凸集。

具体的，若$\chi$为凸集，集合中任意两点$x_1,x_2\in \chi$，则有$t{x}_1+(1-t)x_2\in \chi ,t\in [0,1]$。

反之，若存在$t{x}_1+(1-t)x_2\notin \chi$，则为非凸集合。

二、凸函数和非凸函数

凸函数就是一个定义在某个向量空间的凸子集$\chi$（区间）上的实值函数。对于凸子集$\chi$中任意两个向量$x_1,x_2$有$f((x_1+x_2)/2)\le (f(x_1)+f(x_2))/2$成立。常见的凸函数有：指数函数，非负对数函数，仿射函数，二次函数，常见的范数函数，凸函数非负加权的和等。

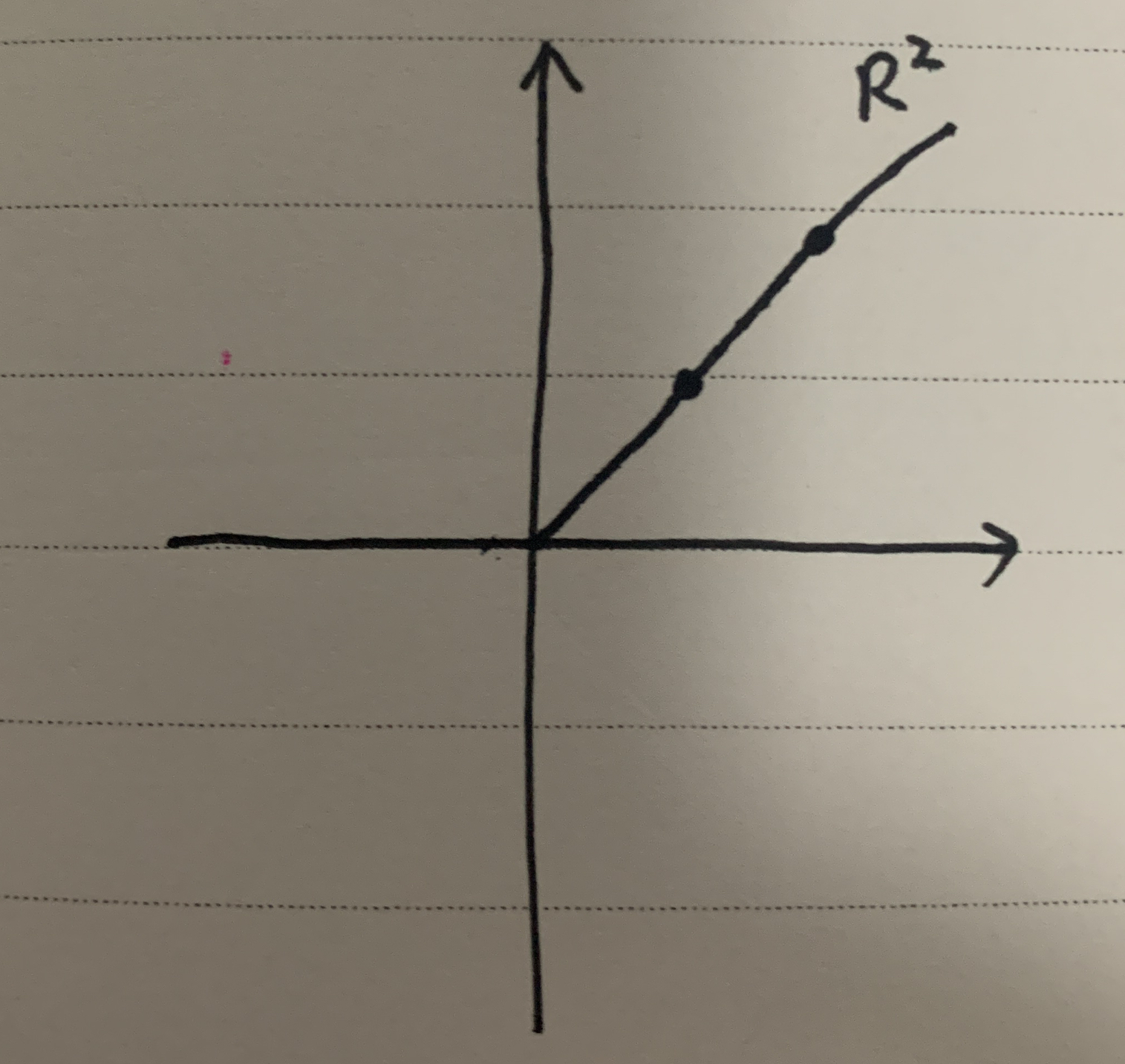
一个典型的凸函数$y=-x^2$，任意两点连线上所有的点都在函数图像的下方，如下图：
非凸函数$y=sin(x)$，两点连线上的点可能分布在函数图像的两侧，如下图：

三、凸优化和非凸优化

凸优化：

任何局部最优解即为全局最优解。通常使用一个局部优化算法，如贪婪算法（Greedy Algorithm）或梯度下降算法（Gradient Decent）来计算局部最优解。

实际问题中，判断是否凸优化问题可以参考以下几点：

• 目标函数$f$如果不是凸函数，则不是凸优化问题。
• 决策变量$x$中包含离散变量（0-1变量或整数变量），则不是凸优化问题。
• 约束条件写成$g(x)\le 0$时，$g$如果不是凸函数，则不是凸优化问题。

常见的凸优化方法：

1. 线性规划(LP, Linear Programming)：
$$\begin{gathered} min{c}^{T}x+d \\ s.t.G(x)⪯h \\ A(x)=b \end{gathered}$$
其中目标函数和不等式约束都是仿射函数（最高次数为1的多项式函数），且$⪯$表示按元素小于等于。

2. 二次规划(QP, Quadratic Programing)：
$$\begin{gathered} min\frac{1}{2}{x}^{T}Px+c^{T}x+d \\ s.t.G(x)⪯h \\ A(x)=b \end{gathered}$$
其中目标函数为凸二次型，不等式约束为仿射函数。

3. 二次约束的二次规划(QCCP, Quadratically Contrained Quaratic Programing)：
$$\begin{gathered} min\frac{1}{2}{x}^{T}Px+c^{T}x+d \\ s.t.\frac{1}{2}{x}^T{Q}_{i}x+r_{i}x+s_i\le 0,i=1,2,...m \\ A(x)=b \end{gathered}$$
其中目标函数和不等式约束都是凸二次型。

4. 半正定规划(SDP, Semidefinite Programing)：
$$\begin{gathered} mintr(CX) \\ s.t.tr(A_{i}X)=b_i,i=1,2,...p \\ X⪰0 \end{gathered}$$
其中需要最优化的变量$X$是一个对称的半正定矩阵，且$C,A_1,...,A_p$为对阵矩阵。

凸优化的一般求解过程

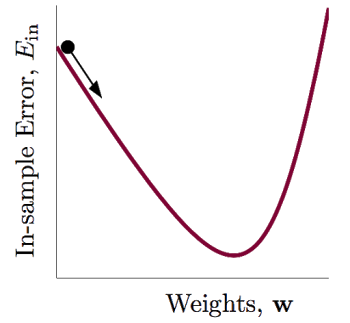
找到一个点列使得目标函数值持续减少，直到触发停止条件或达到一个最小值。

设为$x_k$第k次迭代的值，$d_k$为第k次搜索方向，${\alpha }_k$为第k次迭代的步长，则第k次迭代公式为：
$$x_{k+1}=x_k+{\alpha }_k{d}_k$$
其中第k次的搜索方向满足：
$$\begin{gathered} ▽f(x_k{)}^T{d}_k<0 \\ f(x_{k+1})=f(x_k+{\alpha }_k{d}_k)<f(x_k) \end{gathered}$$

非凸优化：

通常情况下较难求解，可行域集合可能存在无数个局部最优点，求解全局最优算法复杂度是指数级（NP hard）。

因为非凸优化的难度较高，可以考虑将非凸优化转化为凸优化问题解决：

• 修改目标函数，使之转化为凸函数。
• 抛弃一些约束条件，使新的可行域为凸集并且包含原可行域。