目录
13.1二元Logistic回归分析
案例延伸
延伸1：设定模型预测概率得具体值
延伸2：使用Probit模型对二分类因变量进行拟合
13.2多元Logistic回归分析
案例延伸
延伸：根据模型预测每个样本视力低下程度的可能性
13.3有序Logistic回归
案例延伸
延伸：试用Probit模型对有序分类因变量进行拟合
前面我们讲述得回归分析方法都要求因变量是连续变量，但很多情况下因变量是离散得而非连续得。例如，公司招聘人才时根据对应聘人员得特征做出录用或者不录用得评价、毕业学生对职业得选择等。这时就需要用到Logistic回归分析。根据因变量得离散特征：常用得Logistic回归分析方法有3终，包括二元Logistic回归分析、多元Logistic回归分析以及有序Logistic回归分析等。
13.1二元Logistic回归分析
我们经常会遇到因变量只有两种取值的情况，例如是否患病、是否下雨等，这时一般的线性回归分析将无法准确刻画变量之间的因果关系，需要用其他的回归分析方法来进行拟合模型。Stata的二项分类Logistic回归便是一种简便的处理二分类因变量问题的分析方法。
数据（案例13.1）给出了20名肾癌患者的相关数据。试用二分类Logistic回归分析方法分析患者肾细胞转移情况（有转移y=1、无转移y=0）与患者年龄、肾细胞癌血管内皮生长因子（其阳性表示由低到高3个等级）、肾细胞核组织学分级（由低到高共4级）、肾细胞癌组织内微血管数、肾细胞癌分期（由低到高共4期）之间的关系。
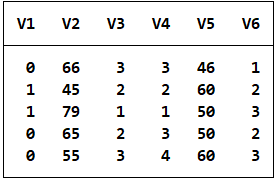
logit V1 V2 V3 V4 V5 V6 #本命令的含义时以V1为因变量，以V2 V3 V4 V5 V6 为自变量，进行二元Logistic回归分析，研究变量之间的因果影响关系。其中自变量的影响是以回归系数的形式输出的。 
从上述分析结果可以看出由20个样本参与了分析，模型的F值（5，14）=1.64，P值（Prob > F）= 0.2135，说明模型整体是不显著的。模型的可决系数（R-squared）为0.3695，模型的修正的可决系数（Adj R-squared）为0.1444，说明模型的解释能力也是比较差的。下面的不过多赘述哈。我们可以看出最小二乘线性模型的整体显著性、系数显著性以及模型的整体解释能力都是由较大提升看空间的。
可以得到最小二乘回归方程模型是：
V1 = -0.0061692*V2+。。。+0.7871698
logistic V1 V2 V3 V4 V5 V6 #本命令的含义是进行二元Logistic回归分析，研究变量之间的因果关系。其中自变量的影响是以（Odds Ratio）的形式输出的。
上图是以V1为因变量，以V2 V3 V4 V5 V6 为自变量，进行二元Logistic回归分析。其中，自变量的影响是以优势比（Odds Ratio）的形式输出的。从上图可以看出Logistic相对于最小二乘回归模型得到了很大程度的改进。。模型的整体显著性P值达到了9%左右（Prob > chi2 = 0.0934）伪R方达到了35%（Pseudo R2 = 0.3500），解释能力得到了进一步提高。各个变量系数的显著程度也有不同程度的提高。
与一般的回归形式不同，此处自变量的影响是以优势比的形式输出的。它的含义是：在自变量保持不变的条件下，被观测自变量每增加1个单位时y=1的发成比的变化倍数。可以看出，各个变量中只有V6变量的增加回引起因变量取1值得大于1倍得增加，这说明只有V6是与因变量呈现正向变化，只有V6使得因变量取1得概率更大。
logit V1 V2 V3 V4 V5 V6 #本命令得含义是进行二元Logistic回归分析，研究变量之间得因果影响关系。其中变量得影响是以回归系数得形式输出得。
上图可以看出该模型与使用Logistic命令回归得到得结果是一致得，只是自变量影像输出得形式由优势比换成了回归系数。
最终模型表达式为：
LNV1 = -0.0644172*V2+...+3.224457
其中LNV1 V2 V3 V4 V5 V6 分别表示肾细胞发生癌转移概率得对数值、年龄、肾细胞癌血管内皮生长因子、肾癌细胞核组织学分级、肾细胞癌组织内微血管数和肾细胞癌分期。
综上所述，我们得到得结论是：年龄、肾细胞癌血管内皮生长因子、肾癌细胞分级、肾细胞癌组织内微血管数与肾细胞癌转移呈反向变化，肾细胞癌分期与肾细胞癌转移呈正向变化，但这些变化并不是特别显著。
estat clas #本命令得含义是计算预测准确得百分比，并提供分类统计和分类表lstat #本命令是上条命令“estat clas”得另一种表达形式
从上图我们可以看出很多信息。按照系统默认设置，系统使用0.5作为分割点。分类中得D、-D、“+”、“-”分别表示以下含义：
D：表示一个观测样本所关注得事件确实发生了，也就是说Y得值去到了1，在本例中，也就是说肾细胞确实发生了癌转移。
-D：表示一个观测样本所关注得事件的确没有发生，也就是说Y得值渠道了0，在本例中，也就是说肾细胞的确没有发生癌转移
+：表示模型预测得概率值大于分割点，本例中，也就是说模型预测得肾细胞发生癌转移得概率为0.5或者更多。
-：表示模型预测得概率值小于分割点，本例中，也就是说模型预测的肾细胞发生癌转移得概率低于0.5。
所以按照模型预测肾细胞发生癌转移得概率至少在0.5以上得标准，有6次是肾细胞确实发生了癌转移而且模型预测得概率值大于分割点，有10次是肾细胞确实没有发生癌转移而且模型预测得概率值小于分割点，所以，一共有16个样本得预测是正确得，预测正确率占全部样本得80%。有2次肾细胞确实发生了癌转移但模型预测得概率值小于分割点，有2次肾细胞确实没有发生癌转移但模型预测得概率值大于分割点，一共有4个样本得预测是错误得，预测错误了占全部样本的20%。
predict yhat #本命令旨在估计因变量得拟合值。它创建一个命名为yhat得新变量，等于最近一次Logistic模型基础上y=1得预测概率 
二元Logistic得因变量拟合值预测结果表示得含义是y=1得概率，本例所表示得含义是肾细胞发生癌转移得概率。
estat gof #本米兰旨在判断模型得拟合效果或者说模型得解释能力
可以看到Prob > chi2 = 0.3503，说明模型得解释能力还是差强人意得，但比最小二乘线性回归模型要好处很多。
案例延伸
延伸1：设定模型预测概率得具体值
estat clas,cutoff(0.8)r延伸2：使用Probit模型对二分类因变量进行拟合
probit V1 V2 V3 V4 V5 V6 #使用Probit回归分析，研究变量之间得因果影响关系
Probit模型与Logistic模型所得得结果相差不大，模型整体得显著程度和解释能力都相比最小二乘回归分析有所提高。
mfx #本命令旨在计算在样本均值处得边际效应Probit模型在样本均值处得标记效应与最小二乘回归分析相差不大。
estat clas #计算预测百分比，并提供分类统计和分类表predict yhat #估计因变量得拟合值。它创建一个yhat变量，等于最近一次Probit模型基础上y=1得预测概率上述结果不过多赘述。
13.2多元Logistic回归分析
我们经常回遇到因变量有多个取值而且无大小顺序得情况，例如职业、婚姻情况等，这时一般得线性回归分析无法准确得刻画变量之间得因果关系，需要用其他得回归分析方法来进行拟合模型。多项分类Logistic回归便是一种简便处理该类因变量问题的分析方法。
数据（案例13.2）给出了山东省某中学20名视力低下学生视力监测的结果数据。试用多项分类Logistic回归分析视力低下程度（由轻到重共3级）与年龄、性别（1代表男性2代表女性）之间的关系。
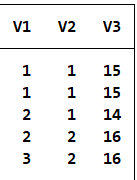
reg V1-V3 #对数据进行最小二乘回归分析
mlogit V1 V2 V3,base(1) #本命令的含义是以V1为因变量，以V2 V3 为自变量，并设定第一组为参照组（视力低下程度为1），进行多元Logistic回归分析，研究变量之间的因果影响关系。其中自变量是以回归系数的形式输出的
从上图可以看出Logistic模型与最小二乘回归估计效果相差不大。模型的整体显著性达到了0.0079（prob > chi2 = 0.0079）。伪R方达到了33.58%（Pseudo R2 = 0.3358）解释能力进一步提高。
从上图分析结果可以看到V2和V3系数在第2组和第3组都是大于0的，这意味着V2和V3两个变量的值越大就越容易被分到2，3组，这表示性别为女年龄越大，越容易被分到中度视力低下，重度视力低下组。
最终模型方程为：
G1=0 因为轻度时因变量重的参考组，其所有系数均为0
G2=LOG[P(低下中度)/P(低下轻度)]=-14.82979+0.8356566*年龄+0.732262*性别1
G3=LOG[P(低下重度)/P(低下轻度)]=-71.13788+2.112522*年龄+18.39871*性别1
mlogit V1 V2 V3,base(1)rrr #本命令的含义是以V1为因变量，以V2 V3 为自变量，并设定第一组为参照组（视力低下程度为1），进行多元Logistic回归分析，研究变量之间的因果影响关系。其中自变量是以相对风险比率的形式输出的
与二元Logistic的优势比（Odds Ratio）的概念类似，相对风险比率的含义是：在其他自变量保持不变的条件下，被观测自变量每增加1个单位y=1的发生比的变化倍数。可以看出，当B2增加或者性别为女生时，他会有相当大的概率会被分到第三组，即重度视力低下，当年龄偏大时，它也有较大概率被分到第三组，即重度视力低下。
案例延伸
延伸：根据模型预测每个样本视力低下程度的可能性
predict eye1 eye2 eye3 
如图所示，第一个观测样本为男性，15岁，他有80%的概率进入第一组，即轻度视力低下，有极小的甚至可以忽略不记得概率被分到第三组，即重度视力低下。其他得观测样本，可以按照类似得方法逐一进行分析，可以看出，我们得模型构建得不错，模型得预测能力也是比较优秀得。
13.3有序Logistic回归
在有些分析研究中，因变量虽然离散但存在这一定得排序，例如消费者对服务行业满意度得评价（很满意、基本满意、不满意、很不满意），又例如消费者对某种品牌产品得忠诚度得衡量（很喜欢、比较喜欢、不喜欢、很不喜欢）。在上述情况下，使用最小二乘回归分析以及二元或多元Logistic回归分析都不能获得比较好得效果，这时就需要用到我们得有序Logistic。
数据（案例13.3）为了获得消费者得满意情况，某公司对120为随机抽取得消费者进行了调查，其中回收有效样本114个，相关信息如图所示，试用有序Logistic回归方法分析消费者满意程度（1表示很满意、2表示基本满意、3表示不满意）与性别（1代表男生，2代表女生）、学历（1表示大学专科及以下，2表示大学本科，3表示研究生及以上）之间得关系。
reg V1-V3 #对数据进行最小二乘回归分析
ologit V1 V2 V3 #本命令得含义时以V1为因变量，以V2 V3 为自变量，进行有序Logistic回归分析，研究变量之间得因果影响关系。
可以看出有序Logistic模型与最小二乘回归估计效果相差不大。模型得整体显著性P值远远低于5%伪R方达到了45.54%。
从图中可以看出V2和V3得系数在第二组和第三组都是大于0得，这意味着V2和V3两个变量的值越大越容易分到后面的组，表示性别为女，学里越高，越容易被分到消费者满意程度较低得组。
cut1 / cut2 表示得含义是割点的估计值，两个割点把样本分成了3个区间，也就是消费者3个不同的满意程度。当样本的因变量拟合值在cut1 之下时，他被分到第1组，消费者满意度为最高；当样本介于 cut1 和 cut2 之间时，它被分到第2组，满意度为中等；当样本的因变量拟合值在cut2之上时，它被分到第3组。消费满意程度为最低。
predict sat1 sat2 sat3
如图所示，第一个观测样本为男性，学历为学学专科以下，他又88%的概率进入第1组，即消费者满意程度为最高，又极小可能甚至忽略的概率进入第3组，即消费者满意程度最低。
案例延伸
延伸：试用Probit模型对有序分类因变量进行拟合
oprobit V1 V2 V3 #进行probit回归分析predict sat11 sat22 sat33 #估计因变量的拟合值。它创建一个命名为yhat的新变量，等于最近一次probit模型基础上y=1的预测概率结果不再过多赘述。
