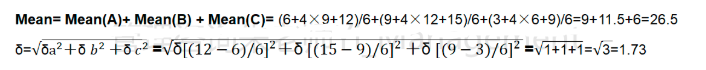一、背景
三点估算使我们在PMP考试中,进度、成本知识领域里常用的技术工具。估算进度、成本时,经常会面临历史数据不充分,这就导致估算充满风险和不确定性,为克服这个问题,提高估算准确性,PMP引入了三点估算法;三点估算充分考虑了风险与不确定性,对同一活动、工作包进行“最乐观、最悲观、最可能”三种估算,在3个估算基础上,引入了“3角分布与贝塔分布”公式,计算预期(平均)的完工持续时间或成本。本文将对此展开讨论。
二、三点估算概述
2.1、基础概念
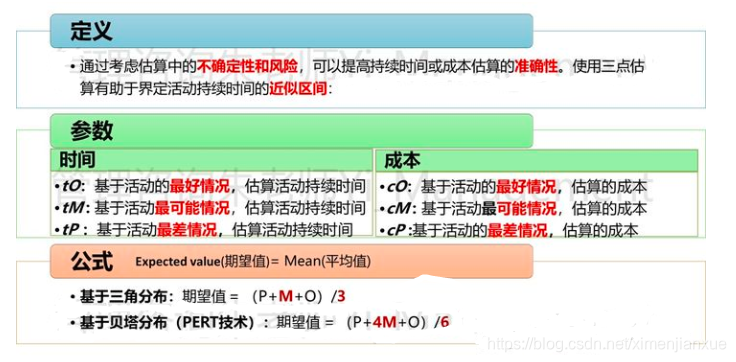
三点估算法,也叫PERT (Program Evaluation and Review Technique) 估算法,即 “计划评估和审查技术”。在估算活动工期或活动成本时,考虑三种可能的情况(最乐观—好,最坏—差,一般)三种情况,得出“最乐观工期、最悲观工期、最可能工期”,再据此计算期望工期(平均工期)。
2.2、时间与成本参数

那么期望值计算公式:

三点估算计算期望值,需要注意2点:
用三点估算计算出完成某活动的的期望值,即有50%的概率,即可能性在该工期内完成。
PMBOK上进度估算选择了三角分布,成本估算选择了贝塔分布;但是鉴于贝塔分布比三角分布计算更科学,很多业界大咖老师认为三点估算,考试中如无特别说明考试工期是呈三角分布的,在默认情况下,首选贝塔分布。
2.3、正态分布图:单一活动
无论三角分布,还是贝塔分布,计算出来的完成某活动的期望工期(平均工期),都只有50%可能性(概率)在该工期内完工。为进一步计算不同时间内,或不同时间变动区间内的完工概率,引入正太分布图进行呈现,正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
图形的中间线条最高对应数值代表期望工期(平均工期),用±δ绘制其他坐标数值,δ代表标准差。
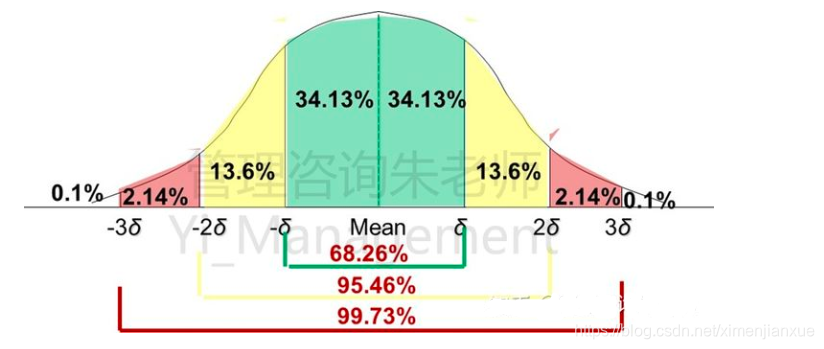
从正太分布图中我们可以看出完工概率分布,与标准差数量的直接联系。
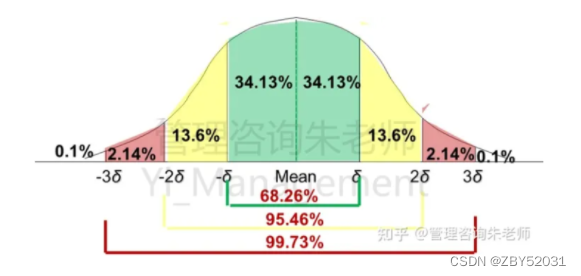
1.如果用1个标准差(±1δ)估算工期,任务或活动在“平均工期±1δ”内完工的概率的概率是68.26%;
2.如果用2个标准差(±2δ)估算工期,任务或活动在“平均工期±2δ”内完工的概率,概率是95.46%;3.如果用3个标准差(±3δ)估算工期,任务或活动在就是“平均工期±3δ”内完工的概率,概率是99.73%;这3个概率可以用下图来理解加深记忆。现在假设,期望工期100天,标准差4天,则可以绘制下表。
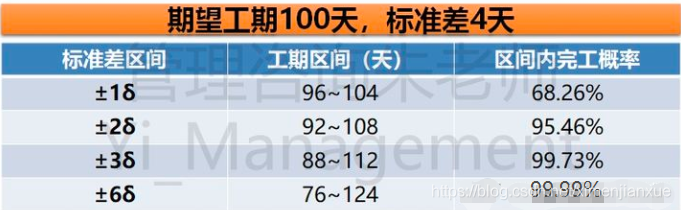
结合上述2图形,我们可以知道,不同时间内的完工概率,如下:
96~104天(±1δ)内完工概率68.26%;
92~108天(±2δ)内完工概率95.46%;
88天~112天(±3δ)内完工概率是99.73%;
96~100天内(-1δ)完工概率是34.13;
100天~104天内(+1δ)完工概率是34.13;
104天内完工概率=50%+(68.26%/2)=84.13%
96天内完工概率=50%-(68.26%/2)=15.87%
92天内完工概率=50%-(95.46%/2)=2.27%
92天96天(-2δ-1δ)内完工概率=15.87%-2.27%=13.6%
2.4、正态分布图—项目工期
知道单个活动工期与概率后,我们就可以根据给出多个活动的P、M、O,求多个活动在给定时间内完工概率。比如计算同一条关键路径上全部活动(不含提前与滞后量)的工期与概率。这时需要计算出“多个活动的平均工期与多活动的标准差”,其中多活动的平均工期就是“活动平均工期之和”,标准差是“对多活动方差之和算根号”。

例子:活动ABC是关键路径,完成活动A乐观时间6天、最可能时间9天、最悲观时间12天,完成活动B乐观时间9天、最可能时间12天、最悲观时间15天,完成活动C乐观时间3天、最可能时间6天、最悲观时间9天;关键路径ABC的平均工期与标准差?