说明

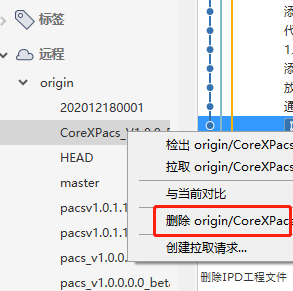
本文并不是严格的证明，只是简单的用于理解什么时候用$dx$什么时候用$ds$，所以采用的曲线比较特殊，为$y=x$并且在$[0,1]$区间上，实际对于复杂的曲线，取微元时$\Delta y$与$\Delta x$为线性关系，即$\Delta y=\alpha \Delta x$，在本文中$\Delta y=\Delta x$。
将区间划为$n$个小区间，对于区间$[a,b]$，每个区间$\Delta x=\frac{b-a}{n}$，区间的左端点为$a+\frac{i}{n}(b-a)$，右端点为$a+\frac{i+1}{n}(b-a)$， i 的 取 值 为 { 0 , 1 , 2 , . . . , n − 1 } i的取值为\{0,1,2,...,n-1\} i的取值为{0,1,2,...,n−1}，而对于本例中，区间范围为$[0,1]$，每个区间$\Delta x=\frac{1}{n}$，区间的左端点为$\frac{i}{n}$，右端点为$\frac{i+1}{n}$。

面积与弧长的情况

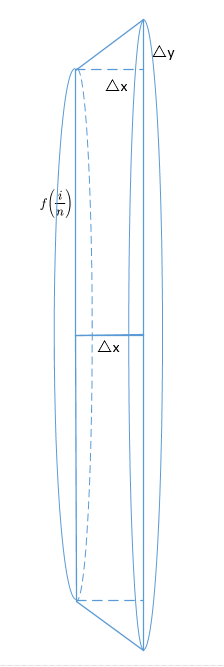
取一小段区间，$\Delta x=\frac{1}{n}$，如图所示，放大来看

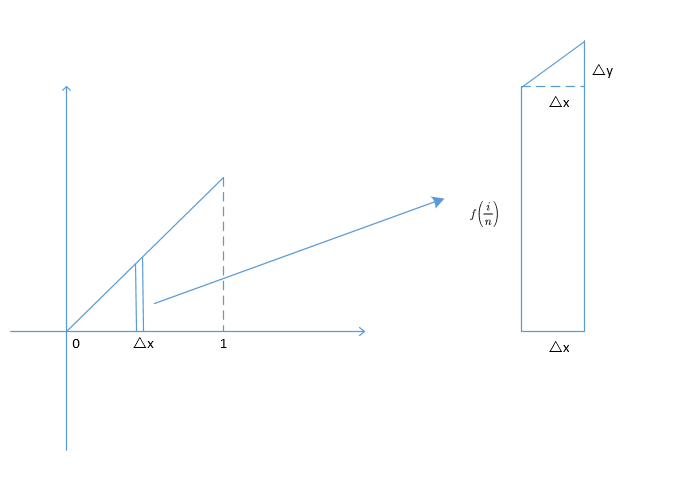
面积

$$\Delta A=f\left(\frac{i}{n}\right)\cdot \Delta x+\frac{1}{2}\cdot \Delta x\cdot \Delta y=f\left(\frac{i}{n}\right)\cdot \frac{1}{n}+\frac{1}{2}\cdot \frac{1}{n}\cdot \frac{1}{n}$$
$$\begin{array}{rl}A& =\underset{n\to +\infty }{\lim }\left(\sum _{i=0}^{n-1}\left(f\left(\frac{i}{n}\right)\cdot \frac{1}{n}\right)+\frac{1}{2}\cdot \frac{1}{n}\cdot \frac{1}{n}\cdot n\right)\\ & =\underset{n\to +\infty }{\lim }\left(\frac{1}{n}\cdot \sum _{i=0}^{n-1}f\left(\frac{i}{n}\right)+\frac{1}{2}\cdot \frac{1}{n}\right)\\ & =\underset{n\to +\infty }{\lim }\left(\frac{1}{n}\cdot \sum _{i=0}^{n-1}f\left(\frac{i}{n}\right)\right)+\underset{n\to +\infty }{\lim }\frac{1}{2n}\end{array}$$

由于$\underset{n\to +\infty }{\lim }\frac{1}{2n}=0$
所以
$$A=\underset{n\to +\infty }{\lim }\left(\frac{1}{n}\cdot \sum _{i=0}^{n-1}f\left(\frac{i}{n}\right)\right)$$
由定积分的定义得
$$A=\underset{n\to +\infty }{\lim }\left(\frac{1}{n}\cdot \sum _{i=0}^{n-1}f\left(\frac{i}{n}\right)\right)={\int }_0^{1}f\left(x\right)dx$$

弧长

$$\Delta S=\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}$$

$$\begin{array}{rl}S& =\underset{n\to +\infty }{\lim }\left(\sum _{i=0}^{n-1}\sqrt{{\left(\Delta x\right)}^2+{\left(\Delta y\right)}^2}\right)\\ & =\underset{n\to +\infty }{\lim }\left(\sum _{i=0}^{n-1}\sqrt{1+{\left(\frac{\Delta y}{\Delta x}\right)}^2}\cdot \Delta x\right)\\ & ={\int }_0^1\sqrt{1+{\left[f^{\prime }\left(x\right)\right]}^2}dx\\ & ={\int }_{s}ds\end{array}$$

旋转体体积和表面积的情况

$y=x$在区间$[0,1]$上绕x轴旋转

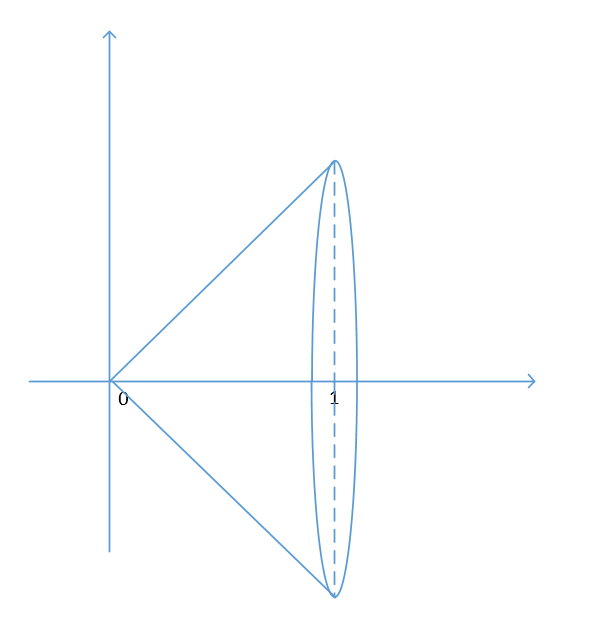
则取一小段区间是一个圆台，图画的不是很好，但可以看出这个圆台的上底面半径为$f\left(\frac{i}{n}\right)$ ，下底面半径为$f\left(\frac{i}{n}\right)+\Delta y$，高位$\Delta x$。

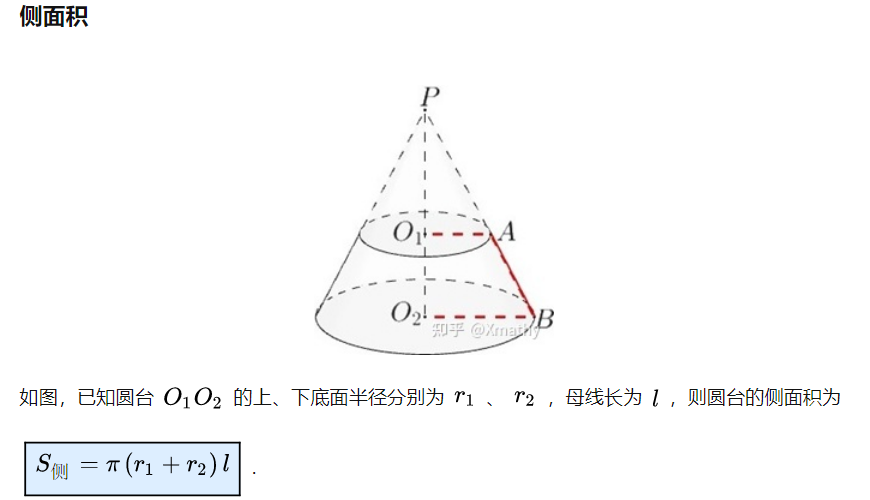
圆台侧面积和体积公式见
公式推导——圆台的侧面积和体积
本文直接给出

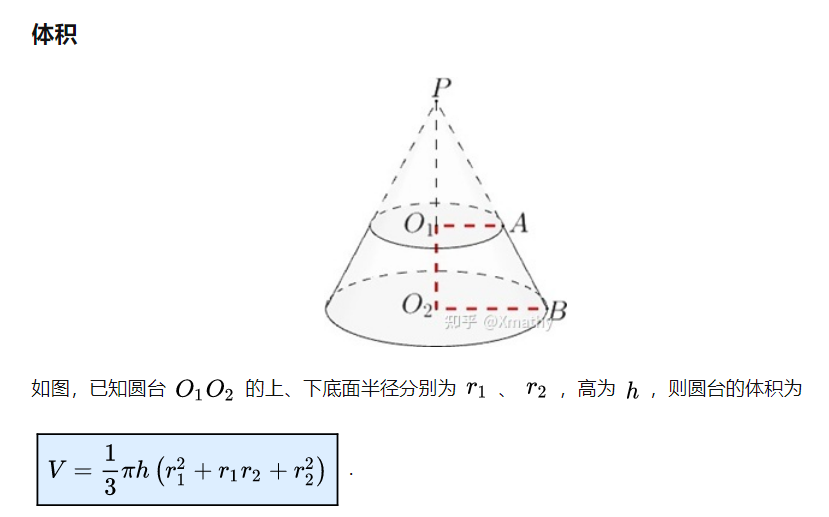
体积

$$\begin{array}{rl}\Delta V& =\frac{1}{3}\pi \Delta x\left[f^2\left(\frac{i}{n}\right)+f\left(\frac{i}{n}\right)\cdot \left(f\left(\frac{i}{n}\right)+\Delta y\right)+{\left(f\left(\frac{i}{n}\right)+\Delta y\right)}^2\right]\\ & =\frac{1}{3}\pi \Delta x\left[f^2\left(\frac{i}{n}\right)+f^2\left(\frac{i}{n}\right)+f\left(\frac{i}{n}\right)\cdot \Delta y+f^2\left(\frac{i}{n}\right)+2\cdot f\left(\frac{i}{n}\right)\cdot \Delta y+{\left(\Delta y\right)}^2\right]\\ & =\frac{1}{3}\pi \Delta x\left[3\cdot f^2\left(\frac{i}{n}\right)+3\cdot f\left(\frac{i}{n}\right)\cdot \Delta y+{\left(\Delta y\right)}^2\right]\\ & =\pi \cdot f^2\left(\frac{i}{n}\right)\cdot \Delta x+\pi \cdot f\left(\frac{i}{n}\right)\cdot \Delta x\cdot \Delta y+\frac{1}{3}\pi \Delta x\cdot {\left(\Delta y\right)}^2\end{array}$$

$$\begin{array}{rl}V& =\underset{n\to +\infty }{\lim }\left[\sum _{i=0}^{n-1}\left(\pi \cdot f^2\left(\frac{i}{n}\right)\cdot \Delta x\right)+\sum _{i=0}^{n-1}\left(\pi \cdot f\left(\frac{i}{n}\right)\cdot \Delta x\cdot \Delta y\right)+\sum _{i=0}^{n-1}\left(\frac{1}{3}\pi \Delta x\cdot {\left(\Delta y\right)}^2\right)\right]\\ & =\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot f^2\left(\frac{i}{n}\right)\cdot \Delta x\right)+\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot f\left(\frac{i}{n}\right)\cdot \Delta x\cdot \Delta y\right)+\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\frac{1}{3}\pi \Delta x\cdot {\left(\Delta y\right)}^2\right)\end{array}$$

其中
$$\because \underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left|\left(\pi \cdot f\left(\frac{i}{n}\right)\cdot \Delta x\cdot \Delta y\right)\right|\le \underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left|\left(\pi \cdot \max \left(f\left(x\right)\right)\cdot \Delta x\cdot \Delta y\right)\right|$$
$$\text{由于分母的数量级为}{n}^2\text{，分子的数量级为}n\text{，所以当}n\to +\infty \text{时}$$
$$\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left|\left(\pi \cdot \max \left(f\left(x\right)\right)\cdot \Delta x\cdot \Delta y\right)\right|=0$$
$$\therefore \underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot f\left(\frac{i}{n}\right)\cdot \Delta x\cdot \Delta y\right)=0$$
显然
$$\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\frac{1}{3}\pi \Delta x\cdot {\left(\Delta y\right)}^2\right)=0$$
所以
$$V=\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot f^2\left(\frac{i}{n}\right)\cdot \Delta x\right)={\int }_0^1\pi x^{2}dx$$

表面积

$$\Delta A=\pi \left(f\left(\frac{i}{n}\right)+f\left(\frac{i}{n}\right)+\Delta y\right)\Delta s=\pi \left(2f\left(\frac{i}{n}\right)+\Delta y\right)\Delta s$$
$$\begin{array}{rl}A& =\underset{n\to +\infty }{\lim }\left[\sum _{i=0}^{n-1}\left(\pi \left(2f\left(\frac{i}{n}\right)+\Delta y\right)\Delta s\right)\right]\\ & =\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot 2f\left(\frac{i}{n}\right)\cdot \Delta s\right)+\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot \Delta y\cdot \Delta s\right)\end{array}$$
其中
$$\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot \Delta y\cdot \Delta s\right)=0$$
则
$$A=\underset{n\to +\infty }{\lim }\sum _{i=0}^{n-1}\left(\pi \cdot 2f\left(\frac{i}{n}\right)\cdot \Delta s\right)={\int }_{s}2\pi f\left(x\right)ds$$

总结

其实不管是求面积还是体积的时候不是想当然的不考虑那一小块（这是很多人误解的地方，从而导致分不清什么时候用$dx$，什么时候用$ds$），而是在求定积分的时候（本质是求极限）那一部分趋于0，所以在实际计算的时候可以忽略趋于0的部分。