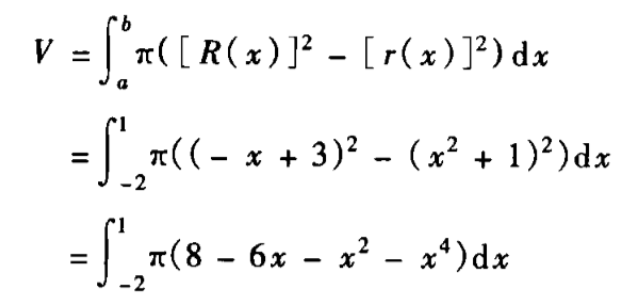三点估算=(乐观+悲观+4*可能)/6
标准差=(悲观-乐观)/6其实还有一个方差的,但是题目中没看到,我就放弃了!网上看到公式是这样的:

放出来混个眼熟吧!大家自行决定要不要记。接下来还有一张图也很重要:
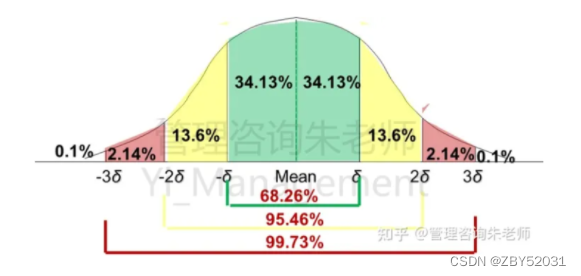
就这样干看公式好像不太理解,那就来些题目。
【试题一】
项目的预期成本是10,000 美元,最乐观的成本估算为5,000 美元,最可能的成本估算为9,000 美元。那么该项目最悲观的成本估算是多少呢?
A. 15,000 美元
B. 16,000 美元
C. 19,000 美元
D. 17,000 美元
三点估算=(悲观+乐观+可能*4)/6
(悲观+5000+9000*4)/6 = 10000
悲观+5000+36000 = 10000*6
悲观 = 60000-36000-5000
悲观 = 19000
有点理解了,那就继续。
【试题二】
项目经理小李对一个小项目的工期进行估算时,发现开发人员的熟练程度对工期有较大的影响,如果都是经验丰富的开发人员,预计20天可以完成;如果都是新手,预计需要38天;按照公司的平均开发速度,一般26天可以完成。该项目的工期可以估算为( )天
A、26 B、27 C、28 D、29
三点估算=(悲观+乐观+可能*4)/6=(20+38+26*4)/6=162/6=27
上面题分析一下【题目比较长,语文不好的我读了好几遍也不知道怎么算】
经验丰富的开发人员,预计20天可以完成
那就可以理解为【乐观】那么乐观=20新手,预计需要38天
那就可以理解为【悲观】那么悲观=38公司的平均开发速度,一般26天可以完成
那就可以理解为【可能】那么可能=26然后理解完,我们看到出现乐观悲观就要想起三点估算这样应该超级简单了吧!读懂题目解题就很简单的。
【试题三】
某项目预计最快12天完成,最慢36天完成,21天完成的可能性最大。公司下达的计划是18天完成,要使计划完成的概率达到50%,在计划中需要增加( )天应急时间。
A、 4 B、6 C、 8 D、22
看完题目是不是有点不了解,没关系!
反正我们看到了可能【21】还有乐观【最快12】和悲观【最慢36】
那就直接套三点估算公式!
三点估算=(悲观+乐观+可能*4)/6
= (12+36+21*4)/6
= 132/6
=22 【均值/平均工期】
标准差=(悲观-乐观)/6 =(36-12)/6 = 24/6 = 4 ,所以项目在22天完成的概率为50%。
题目中,公司下达的计划是18天完成,所以还需要增加22-18=4天的应急时间
好吧!是不是有点不了解,为什么要计算标准差? 因为
一个标准差完工概率是68.26%,题目中要求的完成的概率达到50%
刚好是一个标准差,所以项目在22天完成的概率为50%。
宝子们理解了吗?实在不理解那就继续来个题目,让你们清清楚楚明明白白的理解一下。
【试题四】
某活动的工期最乐观估算6天,最悲观估算30天,最可能估算为9 天,那么:
问题1:8至16天内完成该活动的概率的是多少?
A.68.26% B.95.46% C.99.73% D.97.73%
(悲观+乐观+可能*4)/6 = (30+6+9*4)/6 = 72/6 =12 【均值,预估平均天数】
(悲观-乐观)/6 = (30-6)/6 = 4 【标准差】
均值加减【+-】一个标准差 ,也就是= 12+-4 【12-4=8 ,12+4=16】
正负1个标准差,8天~16天,这个区间完成活动的概率是68.26%
正负2个标准差,4天~20天,这个区间完成活动的概率是95.43%
正负3个标准差,0天~24天,这个区间完成活动的概率是99.73%
现在聪明的你应该懂了吧!上题其实还有一个第二小问:
问题二:在20天内完成该活动的概率是多少?
A.68.26% B.95.46% C.99.73% D.97.73%
50%+95.46%/2=97.73%
看到这个答案应该有两个问题点
第一个:50%怎么来的
第二个:95.46%
我百度了好几个,发现可能不同的标准差,但是一般差值不会相差太多
还没跟大家演示过正态分布图怎么用呢!宝子们,不会忘了正态分布图吧~

这个就是咯,上题。
【试题五】
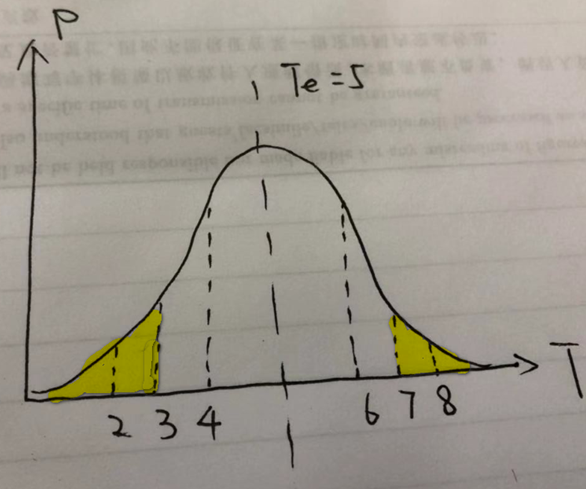
某装修公司给小王装太阳能。M:最可能完成时间为5天,O:最乐观完成时间为2天,P:最悲观完成时间为8天。请问:①平均多长时间完成装修呢?标准差是多少?工期在4天到6天完成的概率是多少?
【三点估算均值/平均时长】:Te = (P+4M+O)/6=(8+4*5+2)/6=5
【标准差】:δ=(P-O)/6=(8-2)/6=1
工期在4天到6天完成的概率(刚好在正负一个标准差内):68.26%
这么多题下来,第一小问对于大家都是小儿科了,那就继续第二小问
②在3天内完成的概率是多少?
其实我们公式也很快 3天内也就2个标准差,也就=(1-95.46%)/2=2.27%
但是我想学画一下图,所以根据第一小问来个正态分布图:
从上图我们可以看出,3天内所对应的区域属于黄色区域
所以概率为:(1-95.46%)/2=2.27%
③最低保证率达到97.5%,需要工期为多少天?
(97.5%-50%)*2=95%
我们从上述结论可以知道2个标准差的概率是95.46%,那么工期=5+2*1=8
所以遇到这类题,先画出正态分布图,也是一个解决问题的好方法!