层次分析法 | 过程解读 案例实践
导读
本文将带领读者了解 AHP 法,通过案例学习,学会使用 AHP 法解决实际问题。在适当的地方将深入了解,例如 AHP 法过程中出现的不一致情况,我们将详细讨论为什么会出现不一致情况,如何验证是否不一致,如何解决不一致情况。
本文无代码实现,更注重 AHP 法过程本身的原理。
文章目录
- 层次分析法 | 过程解读 案例实践
- 导读
- 一. AHP 层次分析法介绍
- 二. AHP 的实际问题应用案例
- 1. 确定评价指标,建立层次关系
- 2. 构造上一层每个节点与下一层的判断矩阵
- 3. 层次单排序及一致性检验
- 4. 层次总排序
- 三. 不一致现象 与 一致性检验
- 四. (补充) 特征值法求相对重要性权重
- 参考文献
一. AHP 层次分析法介绍
-
AHP 层次分析法简介
AHP,即层次分析法(Analytic Hierarchy Process,AHP)是一种系统化的、层次化的多目标综合评价方法。在评价对象的待评价属性复杂多样,结构各异,难以量化的情况下AHP层次分析法也能发挥作用。
-
AHP 基本思想 [1]
AHP 把复杂的问题分解为各个组成因素,又将这些因素按支配关系分组形成地递阶层次结构。通过两两比较的方式确定方式确定层次中诸因素的相对重要性。然后综合有人员的判断,确定备选方案相对重要性的总排序。整个过程体现了入门分解问题—判断—综合,的思想特征。
-
AHP 步骤
- 分析问题,明确需求,确定评价指标,并建立评价层次关系。
- 构造上一层每个节点与下一层的判断矩阵。
- 由判断矩阵得出层间的相对权重(层次单排序及一致性检验)。
- 计算各层对总评价目标的总权重(层次总排序),得出各备选方案的评估结果。
注意
下文中计算数值均四舍五入保留三位小数。一些归一化结果为了保证其结果和为1,可能存在一定的计算误差。但不影响最终结果的准确性
二. AHP 的实际问题应用案例
本章节我们将在选择购买空调的过程中使用 AHP 来完成决策。
为了从三种空调,空调A、空调B、空调C,中选购最合适的空调,我们采用 AHP 法对我们的需求进行分析与评估,最终完成决策。
1. 确定评价指标,建立层次关系
为了选出最合适的空调,我们确定从四个指标来对空调进行评估,分别是:价格、噪声、功耗、寿命。 在 AHP 中,要构建三层层次关系:目标层、准则层、方案层。
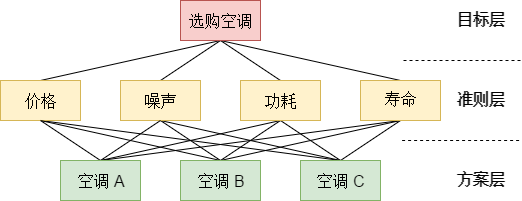
- 目标层
只有一个要素,是分析问题的预期结果或期望实现的最终目标,是评价的最高准则,可称为目的或目标层 - 准则层
准则层可以是多层构成,其包括所要考虑的准则,子准则等。 - 方案层
表示实现目标所提供的各种方案与措施,是最终评价对象,决策的结果将从中选出。
2. 构造上一层每个节点与下一层的判断矩阵
对一层的每一个节点,与其下层的所有与其有关联的节点构建判断矩阵。
判断矩阵描述了下一层节点之间的相对重要性或优越性。为了量化节点间的优劣先后,将用到以下判断矩阵标度定义。
| 标度 | 含义 |
|---|---|
| 1 | 两个要素相比,重要性相同 |
| 3 | 两要素相比,前者比后者稍微重要或有优势 |
| 5 | 两要素相比,前者比后者比较重要或有优势 |
| 7 | 两要素相比,前者比后者十分重要或有优势 |
| 9 | 两要素相比,前者比后者绝对重要或有优势 |
| 2,4,6,8 | 为上述标度之间的中间值 |
| 若要描述后者与前者比较,则用倒数为标度。例如 1/3 描述的是,后者比前者稍微重要。 | |
这么说还是有些抽象,我们用以上标度为规则,来构建目标层与准则层之间的判断矩阵如下。
| 选购空调 | 价格 | 噪声 | 功耗 | 寿命 |
|---|---|---|---|---|
| 价格 | 1 | 1/3 | 1/5 | 1 |
| 噪声 | 3 | 1 | 1 | 5 |
| 功耗 | 5 | 1 | 1 | 5 |
| 寿命 | 1 | 1/5 | 1/5 | 1 |
表中描述的是为了达到目标,准则层节点之间的相对重要程度,决定这些数值大小的可以是决策者的主观判断,也可以是基于调查或文献来判断,也可以是由专家讨论决定,本文中的值都由笔者主观决定。
如,价格行,噪声列(矩阵中坐标为[1,2])值为 1/3 ,意味着价格(前者)的重要程度是噪声(后者)重要程度的 1/3。反过来,我们也可以说相对于价格,噪声的重要程度为 3。
因此判断矩阵是斜对角线对称元素互为倒数的。 并且规定,而在斜对角线上,要素和自身比较的标度恒 1。判断矩阵是一个正互反矩阵。
同样的,需要构建准则层每一个节点到方案层所有节点的判断矩阵。
- 三种空调对于价格的判断矩阵
| 价格 | 空调 A | 空调 B | 空调 C |
|---|---|---|---|
| 空调 A | 1 | 1/7 | 1/5 |
| 空调 B | 7 | 1 | 2 |
| 空调 C | 5 | 1/2 | 1 |
图中 [2,1] 的值为 7 ,意味着空调 B 的价格优势相对于空调 A 十分有优势。 其他同理,下面多个判断矩阵也同理。
- 三种空调对于噪声的判断矩阵
| 噪声 | 空调 A | 空调 B | 空调 C |
|---|---|---|---|
| 空调 A | 1 | 2 | 5 |
| 空调 B | 1/2 | 1 | 4 |
| 空调 C | 1/5 | 1/4 | 1 |
- 三种空调对于功耗的判断矩阵
| 功耗 | 空调 A | 空调 B | 空调 C |
|---|---|---|---|
| 空调 A | 1 | 3 | 1/2 |
| 空调 B | 1/3 | 1 | 1/5 |
| 空调 C | 2 | 5 | 1 |
- 三种空调对于寿命的判断矩阵
| 寿命 | 空调 A | 空调 B | 空调 C |
|---|---|---|---|
| 空调 A | 1 | 1/5 | 1/3 |
| 空调 B | 5 | 1 | 4 |
| 空调 C | 3 | 1/4 | 1 |
注意
- 判断矩阵的值显然只需要填写上半三角区或下半三角区就可以确定整个判断矩阵,请务必保持判断矩阵的 " \ " 向对角线对称的元素互为倒数。
- 标度的定义是谁更重要或有优势,不是直接比较其量的大小。例如在三种空调对于功耗的判断矩阵中,[1,2] 的值为 3,指的不是空调 A 的功耗相对于空调 B 比较有大,这意味着空调 A 比空调 B 更耗电。标度的实际意思是空调 A 的功耗相对于空调 B 比较有优势,这意味着空调 A 比空调 B 更有优势,更省电。
- 判断矩阵的数值不能随便乱填,还需要遵守逻辑规范。例如在三种空调对于寿命的判断矩阵中可知,空调 B 的寿命比空调 C 更有优势,而空调 C 也比 空调 A 更有优势,那么就不能说空调 A 比 空调 B 更有优势,这显然是违背逻辑的 ,为了避免这种逻辑上的差错,我们可以先填矩阵,后利用一致性检验(下文即将介绍)来判断我们的矩阵是否存在逻辑上的错误,若有我们则修改标度。
3. 层次单排序及一致性检验
所谓层次单排序,指的是:根据判断矩阵计算对于上一层的一个节点而言本层次与之有联系的所有节点的重要性次序的权重值,从而根据权重对其进行重要性排序。
我们以目标层与准则层开始。
| 选购空调 | 价格 | 噪声 | 功耗 | 寿命 | w i \mathbf{w}_i wi | w i 0 \mathbf{w}_i^0 wi0 | A w i 0 \mathbf{Aw}_i^0 Awi0 | λ m i \mathbf{λ}_{mi} λmi |
|---|---|---|---|---|---|---|---|---|
| 价格 | 1 | 1/3 | 1/5 | 1 | 0.508 | 0.099 | 0.400 | 4.040 |
| 噪声 | 3 | 1 | 1 | 5 | 1.968 | 0.381 | 1.546 | 4.058 |
| 功耗 | 5 | 1 | 1 | 5 | 2.236 | 0.433 | 1.744 | 4.028 |
| 寿命 | 1 | 1/5 | 1/5 | 1 | 0.447 | 0.087 | 0.349 | 4.011 |
| λ m a x = 4.033 , C . I . = 0.011 , R . I . = 0.89 , C . R . = 0.012 < 0.1 \mathbf{λ}_{max} = 4.033,C.I. = 0.011,R.I. = 0.89,C.R. = 0.012<0.1 λmax=4.033,C.I.=0.011,R.I.=0.89,C.R.=0.012<0.1 |
连续出现了一系列的新值,我们将一一介绍。
-
w i \mathbf{w}_i wi 与 w i 0 \mathbf{w}_i^0 wi0, w i \mathbf{w}_i wi基于判断矩阵计算得出,采用方根法计算,其计算过程为
-
判断矩阵各行元素求几何平均数。
w i = [ 1 × 1 3 × 1 5 × 1 4 3 × 1 × 1 × 5 4 5 × 1 × 1 × 5 4 1 × 1 5 × 1 5 × 1 4 ] = [ 0.508 1.968 2.236 0.447 ] \mathbf{w}_i = \left[ \begin{matrix} \sqrt[4]{1\times\frac{1}{3}\times\frac{1}{5}\times1} \\ \sqrt[4]{3\times1\times1\times5} \\ \sqrt[4]{5\times1\times1\times5} \\ \sqrt[4]{1\times\frac{1}{5}\times\frac{1}{5}\times1} \\ \end{matrix} \right] =\left[ \begin{matrix} 0.508\\ 1.968\\ 2.236\\ 0.447 \end{matrix} \right] wi= 41×31×51×143×1×1×545×1×1×541×51×51×1 = 0.5081.9682.2360.447
-
将 w i \mathbf{w}_i wi 归一化得到要素相对权重 w i 0 \mathbf{w}_i^0 wi0
w 0 = [ 0.508 0.508 + 1.968 + 2.236 + 0.447 1.968 0.508 + 1.968 + 2.236 + 0.447 2.236 0.508 + 1.968 + 2.236 + 0.447 0.447 0.508 + 1.968 + 2.236 + 0.447 ] = [ 0.099 0.381 0.433 0.087 ] \mathbf{w}^0 = \left[ \begin{matrix} \frac{0.508}{0.508+1.968+2.236+0.447}\\ \frac{1.968}{0.508+1.968+2.236+0.447}\\ \frac{2.236}{0.508+1.968+2.236+0.447}\\ \frac{0.447}{0.508+1.968+2.236+0.447} \end{matrix} \right] = \left[ \begin{matrix} 0.099 \\ 0.381 \\ 0.433 \\ 0.087 \end{matrix} \right] w0= 0.508+1.968+2.236+0.4470.5080.508+1.968+2.236+0.4471.9680.508+1.968+2.236+0.4472.2360.508+1.968+2.236+0.4470.447 = 0.0990.3810.4330.087
而对于采用方根法的通用公式为
特征矩阵: A = [ a 11 a 12 ⋯ a 1 n a 21 ⋮ ⋱ a n 1 a n n ] , w i 0 = ( ∏ j = 1 n a i j ) 1 n ∑ i = 1 n ( ∏ j = 1 n a i , j ) 1 n , n = 1 , 2 , ⋯ , n 特征矩阵:A = \left[ \begin{matrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}\\ \vdots&&\ddots\\ a_{n1}&&&a_{nn} \end{matrix} \right] ,\mathbf{w}_i^0 = \frac{(\prod_{j=1}^na_{ij})^{\frac{1}{n}}}{\sum_{i=1}^n (\prod_{j=1}^n a_{i,j})^{\frac{1}{n}}},n=1,2,\cdots,n 特征矩阵:A= a11a21⋮an1a12⋯⋱a1nann ,wi0=∑i=1n(∏j=1nai,j)n1(∏j=1naij)n1,n=1,2,⋯,n
也可以使用求和法计算权重 w i 0 \mathbf{w}_i^0 wi0 ,这里只给出公式不给出本例的计算过程。求和法得到的 w i 0 \mathbf{w}_i^0 wi0 值可能与方根法求到的 w i 0 \mathbf{w}_i^0 wi0 不完全一样,这是正常的。
w i 0 = 1 n ∑ j = 1 n a i j ∑ k = 1 n a i j , n = 1 , 2 , ⋯ , n \mathbf{w}_i^0 = \frac{1}{n}\sum_{j=1}^n\frac{a_{ij}}{\sum_{k=1}^na_{ij}},n = 1,2,\cdots,n wi0=n1j=1∑n∑k=1naijaij,n=1,2,⋯,n
- 将判断矩阵的每列归一化,即 a i j ∑ k = 1 n a i j \frac{a_{ij}}{\sum_{k=1}^na_{ij}} ∑k=1naijaij。
- 将得到的新矩阵求各行的算数平均数得到 w i 0 \mathbf{w}_i^0 wi0
-
-
A w i 0 \mathbf{Aw}_i^0 Awi0 即为判断矩阵 A \mathbf{A} A 与权重 w i 0 \mathbf{w}_i^0 wi0 的矩阵点乘运算结果
A w 0 = [ 1 1 3 1 5 1 3 1 1 5 5 1 1 5 1 1 5 1 5 1 ] ⋅ [ 0.099 0.381 0.433 0.087 ] = [ 0.4 1.546 1.744 0.349 ] \mathbf{Aw}^0 = \left[ \begin{matrix} 1 & \frac{1}{3} & \frac{1}{5} & 1 \\ 3 & 1 & 1 & 5 \\ 5 & 1 & 1 & 5 \\ 1 & \frac{1}{5} & \frac{1}{5} & 1 \end{matrix} \right]· \left[ \begin{matrix} 0.099\\ 0.381\\ 0.433\\ 0.087 \end{matrix} \right]= \left[ \begin{matrix} 0.4\\ 1.546\\ 1.744\\ 0.349 \end{matrix} \right] Aw0= 13513111515111511551 ⋅ 0.0990.3810.4330.087 = 0.41.5461.7440.349
-
λ m i \mathbf{λ}_{mi} λmi 是用于计算 λ m a x \mathbf{λ}_{max} λmax 的中间值,而 λ m a x \mathbf{λ}_{max} λmax 用于一致性检验。
λ m i = A w i 0 w i 0 \mathbf{λ}_{mi} = \frac{\mathbf{Aw}_i^0}{\mathbf{w}_i^0} λmi=wi0Awi0
-
λ m a x \mathbf{λ}_{max} λmax 用于计算后续的 C . I . \mathbf{C.I.} C.I. 值,从而完成一致性检验。
λ m a x = 1 n ∑ i = 1 n λ m i \mathbf{λ}_{max} = \frac{1}{n}\sum_{i=1}^{n}\mathbf{λ}_{mi} λmax=n1i=1∑nλmi
-
C . I . \mathbf{C.I.} C.I. , R . I . \mathbf{R.I.} R.I. 和 C . R . \mathbf{C.R.} C.R. 。 C . I . \mathbf{C.I.} C.I. 为一致性指标, R . I . \mathbf{R.I.} R.I. 为平均随机一致性指标, C . R . \mathbf{C.R.} C.R. 为一致性指标,这些指标用于完成判断矩阵的一致性检验。
C . I . = λ m a x − n n − 1 \mathbf{C.I.} = \frac{\mathbf{λ}_{max}-n}{n-1} C.I.=n−1λmax−n
R . I . \mathbf{R.I.} R.I. 的值要参考平均随机一致性指标表来确定,其值由 n \mathbf{n} n 即判断矩阵的阶 数,查下表得n \mathbf{n} n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 R . I . \mathbf{R.I.} R.I. 0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 本例中 n = 4 \mathbf{n}=4 n=4, R . I . = 0.89 \mathbf{R.I.} = 0.89 R.I.=0.89
C . R . = C . I . R . I . \mathbf{C.R.}=\frac{\mathbf{C.I.}}{\mathbf{R.I.}} C.R.=R.I.C.I.
若 C . R . < 0.1 \mathbf{C.R.} < 0.1 C.R.<0.1 则认为判断矩阵通过了一致性检验,若不满足条件则需要检查判断矩阵,并对其值进行调整。 本例中 C . R . = 0.012 < 0.1 \mathbf{C.R. = 0.012<0.1} C.R.=0.012<0.1,因此通过了一致性检验,可继续进行后续的步骤。
在完成目标层与准则层的层次单排序与一致性检验之后,还需对准则层到方案层的多个判断矩阵进行层次单排序与一致性检验。这里直接给出结果。
-
三种空调对于价格的判断矩阵的层次单排序与一致性检验
价格 空调 A 空调 B 空调 C w i \mathbf{w}_i wi w i 0 \mathbf{w}_i^0 wi0 A w i 0 \mathbf{Aw}_i^0 Awi0 λ m i \mathbf{λ}_{mi} λmi 空调 A 1 1/7 1/5 0.306 0.075 0.226 3.016 空调 B 7 1 2 2.41 0.592 1.783 3.011 空调 C 5 1/2 1 1.357 0.333 1.004 3.015 λ m a x = 3.014 , C . I . = 0.007 , R . I . = 0.52 , C . R . = 0.013 < 0.1 \mathbf{λ}_{max} = 3.014,C.I. = 0.007,R.I. = 0.52,C.R. = 0.013<0.1 λmax=3.014,C.I.=0.007,R.I.=0.52,C.R.=0.013<0.1 -
三种空调对于噪声的判断矩阵的层次单排序与一致性检验
噪声 空调 A 空调 B 空调C w i \mathbf{w}_i wi w i 0 \mathbf{w}_i^0 wi0 A w i 0 \mathbf{Aw}_i^0 Awi0 λ m i \mathbf{λ}_{mi} λmi 空调 A 1 2 5 2.154 0.570 1.721 3.019 空调 B 1/2 1 4 1.26 0.333 1.006 3.021 空调 C 1/5 1/4 1 0.368 0.097 0.294 3.030 λ m a x = 3.023 , C . I . = 0.012 , R . I . = 0.52 , C . R . = 0.023 < 0.1 \mathbf{λ}_{max} = 3.023,C.I. = 0.012,R.I. = 0.52,C.R. = 0.023<0.1 λmax=3.023,C.I.=0.012,R.I.=0.52,C.R.=0.023<0.1 -
三种空调对于功耗的判断矩阵的层次单排序与一致性检验
功耗 空调 A 空调 B 空调C w i \mathbf{w}_i wi w i 0 \mathbf{w}_i^0 wi0 A w i 0 \mathbf{Aw}_i^0 Awi0 λ m i \mathbf{λ}_{mi} λmi 空调 A 1 3 1/2 1.145 0.309 0.927 3.000 空调 B 1/3 1 1/5 0.405 0.109 0.328 3.009 空调 C 2 5 1 2.154 0.582 1.745 3.000 λ m a x = 3.003 , C . I . = 0.0015 , R . I . = 0.52 , C . R . = 0.003 < 0.1 \mathbf{λ}_{max} = 3.003,C.I. = 0.0015,R.I. = 0.52,C.R. = 0.003<0.1 λmax=3.003,C.I.=0.0015,R.I.=0.52,C.R.=0.003<0.1 -
三种空调对于寿命的判断矩阵的层次单排序与一致性检验
寿命 空调 A 空调 B 空调C w i \mathbf{w}_i wi w i 0 \mathbf{w}_i^0 wi0 A w i 0 \mathbf{Aw}_i^0 Awi0 λ m i \mathbf{λ}_{mi} λmi 空调 A 1 1/5 1/3 0.405 0.1 0.310 3.100 空调 B 5 1 4 2.41 0.674 2.078 3.083 空调 C 3 1/4 1 0.909 0.226 0.695 3.075 λ m a x = 3.086 , C . I . = 0.043 , R . I . = 0.52 , C . R . = 0.083 < 0.1 \mathbf{λ}_{max} = 3.086,C.I. = 0.043,R.I. = 0.52,C.R. = 0.083<0.1 λmax=3.086,C.I.=0.043,R.I.=0.52,C.R.=0.083<0.1
注意
在层次单排序过程中的 平均随机一致性表( R . I . \mathbf{R.I.} R.I. 值表)是由蒙特卡洛算法模拟随机矩阵验证一致性是否可以接受得来的。有兴趣的读者可以查询,了解。
总结
完成一个判断矩阵的层次单排序与一致性检验的求值过程为,简单总结如下:
- 选定方法求 w i \mathbf{w_{i}} wi(尚未归一化的权重)
- 归一化 w i \mathbf{w_{i}} wi 得到 w i 0 \mathbf{w_{i}^0} wi0(相对重要性权重)
- 将判断矩阵 A 与 w i 0 \mathbf{w_{i}^0} wi0 矩阵点乘得到 A w i 0 \mathbf{Aw}_i^0 Awi0
- 将 A w i 0 \mathbf{Aw}_i^0 Awi0 除以 w i 0 \mathbf{w_{i}^0} wi0 得到 λ m i \mathbf{λ}_{mi} λmi
- 使用 λ m i \mathbf{λ}_{mi} λmi 求得 λ m a x \mathbf{λ}_{max} λmax
- 利用 λ m a x \mathbf{λ}_{max} λmax 求 C . I . \mathbf{C.I.} C.I.,查表得到 R . I . \mathbf{R.I.} R.I. 对应的值,将 C . I . \mathbf{C.I.} C.I. 与 R . I . \mathbf{R.I.} R.I. 相除得到 C . R . \mathbf{C.R.} C.R.
- 比较 C . R . \mathbf{C.R.} C.R. 与 0.1 的大小,确定是否通过一致性检验,不通过则修改判断矩阵的值,直到通过一致性检验。
- 完成层次单排序,获得结果 w i 0 \mathbf{w_{i}^0} wi0
4. 层次总排序
层次总排序得出了方案层对于目标层的重要程度权重,从而我们可以选出权重最大的为决策结果
| 评价标准 | 价格 | 噪声 | 功耗 | 寿命 | 最终评分 总权重(w) |
|---|---|---|---|---|---|
| 权重 | 0.099 | 0.381 | 0.433 | 0.087 | |
| 空调 A | 0.075 | 0.570 | 0.309 | 0.100 | 0.367 |
| 空调 B | 0.592 | 0.333 | 0.109 | 0.674 | 0.291 |
| 空调 C | 0.333 | 0.091 | 0.582 | 0.226 | 0.342 |
以上表格关于四大评价指标对各空调的权重(第二行)来自于目标层与准则层判断矩阵的层次单排序结果权重。空调 ABC 对于四大评价指标的分别权重来自于准则层到方案层的判断矩阵层次单排序结果权重。表格中的最终得分计算方法是:用各评价指标的权重,乘上某空调各个指标对应的权重求和。以求空调 A 的最终得分为例,公式如下
空调 A 评分 = 0.099 × 0.075 + 0.381 × 0.570 + 0.433 × 0.309 + 0.087 × 0.100 = 0.367 空调 A 评分 = 0.099\times0.075+0.381\times0.570+0.433\times0.309+0.087\times0.100=0.367 空调A评分=0.099×0.075+0.381×0.570+0.433×0.309+0.087×0.100=0.367
空调 BC 的评分同理。因为 w 空调 A > w 空调 C > w 空调 B \mathbf{w_{空调A}}>\mathbf{w_{空调C}}>\mathbf{w_{空调B}} w空调A>w空调C>w空调B,所以我们通过 AHP 法得出购买空调 A 最符合我们的需求。
三. 不一致现象 与 一致性检验
上文中有提到判断矩阵中会出现不一致的现象,也使用计算一致性比例的问题来判断判断矩阵是否出现不一致的现象。本章节将较为详细的分析讲解判断矩阵中出现的不一致现象,并介绍一种和求和法与方根法同样常用的求要素相对权重的方法——特征值法。
正如上文中所提到的不一致现象,我们继续利用空调对寿命的判断矩阵来进行分析。
| 寿命 | 空调 A | 空调 B | 空调 C |
|---|---|---|---|
| 空调 A | 1 | 1/5 | 1/3 |
| 空调 B | 5 | 1 | 4 |
| 空调 C | 3 | 1/4 | 1 |
该判断矩阵在上一章中已经通过一致性检验。但我们仔细分析,会发现该判断矩阵中依然存在不一致的问题。我们进行下列推断
[ 2 , 1 ] = 5 ⇒ 空调 B 比空调 A 比较有优势 [ 3 , 1 ] = 3 ⇒ 空调 C 比空调 A 稍微有优势 则,空调 B 比空调 C 应该稍 微 ① 有优 势 ② [2,1] = 5 \Rightarrow 空调 B 比 空调 A 比较有优势\\ [3,1] = 3 \Rightarrow 空调 C 比 空调 A 稍微有优势\\ 则,空调 B 比 空调 C应该稍微^{①}有优势^{②} [2,1]=5⇒空调B比空调A比较有优势[3,1]=3⇒空调C比空调A稍微有优势则,空调B比空调C应该稍微①有优势②
在结论中有两小点:
-
我们在上文中说明过,如果认为空调 C 比空调 B 更有优势则与②相反,违背了逻辑,这种不一致是不被允许的。假如我们颠倒空调 BC 的优势顺序,得到以下判断矩阵:
寿命 空调 A 空调 B 空调 C 空调 A 1 1/5 1/3 空调 B 5 1 1/4 空调 C 3 4 1 λ m a x = 4.24 , C . I . = 0.62 , R . I . = 0.52 , C . R . = 1.192 > 0.1 \mathbf{λ}_{max} = 4.24,C.I. = 0.62,R.I. = 0.52,C.R. =1.192>0.1 λmax=4.24,C.I.=0.62,R.I.=0.52,C.R.=1.192>0.1 经过计算,发现一致性检验不通过。 若我们将空调 BC 的优势程度写为一样有优势则得到以下判断矩阵:
寿命 空调 A 空调 B 空调 C 空调 A 1 1/5 1/3 空调 B 5 1 1 空调 C 3 1 1 λ m a x = 3.866 , C . I . = 0.433 , R . I . = 0.52 , C . R . = 0.833 > 0.1 \mathbf{λ}_{max} = 3.866,C.I. = 0.433,R.I. = 0.52,C.R. =0.833>0.1 λmax=3.866,C.I.=0.433,R.I.=0.52,C.R.=0.833>0.1 也不通过一致性检验。因此一致性检验确实起到了避免判断矩阵中数值出现逻辑冲突的情况
- 在结论①中,其确定了的是空调 B 比空调 C 优势的程度大小为多少。结论中我们写的是 “稍微有优势”,那么判断矩阵中对应的位置应该是 3 和 1/3,但原题目中判断矩阵对应的位置为 4 和 1/4。我们可以试着计算一下判断矩阵是否通过一致性检验:
寿命 空调 A 空调 B 空调 C 空调 A 1 1/5 1/3 空调 B 5 1 3 空调 C 3 1/3 1 λ m a x = 3.029 , C . I . = 0.0145 , R . I . = 0.52 , C . R . = 0.028 < 0.1 \mathbf{λ}_{max} = 3.029,C.I. = 0.0145,R.I. = 0.52,C.R. =0.028<0.1 λmax=3.029,C.I.=0.0145,R.I.=0.52,C.R.=0.028<0.1 通过一致性检验。而原来的 4 与 1/4 也通过了一致性检验,因此可见在基本的谁比谁有优势确定后,其优势程度大小是有可调节的弹性的。这是因为相对重要性标度本身对于要素之间的优势程度定义是模糊的。
四. (补充) 特征值法求相对重要性权重
上文中有介绍两种求要素相对重要性权重的方法:方根法与求和法。本章介绍一种和这两种同样常用的方法来求权重——特征值法。
-
特征向量与特征值[2]
A 为 n × n 矩阵, x 为非零向量, 若存在数 λ 使得 A x = λ x 有非平凡解 x , 则称 λ 为 A 的特征值, x 称为对应与 λ 的特征向量。 \mathbf{A} 为 \mathbf{n\times n} 矩阵,\mathbf{x} 为非零向量,\\若存在数 \mathbf{\lambda} 使得 \mathbf{Ax=\lambda x} 有非平凡解 \mathbf{x},\\则称 \mathbf{\lambda} 为 \mathbf{A} 的特征值,\mathbf{x} 称为对应与 \mathbf{\lambda} 的特征向量。 A为n×n矩阵,x为非零向量,若存在数λ使得Ax=λx有非平凡解x,则称λ为A的特征值,x称为对应与λ的特征向量。
利用特征值法求相对重要性权重,就是求判断矩阵的特征向量,并将特征向量列归一化,然后直接作为相对重要性权重向量。但这个方法对判断矩阵严格要求其为一致矩阵,而我们上例中的判断矩阵都是不完全一致的,因此不适用此方法(可重新确定判断矩阵的值使其为一致矩阵再用此方法)。 -
一致矩阵
若矩阵 A = [ a 11 a 12 ⋯ a 1 n a 21 ⋮ ⋱ a n 1 a n n ] 满足 : a i j > 0 a 11 = a 22 = ⋯ = a n n = 1 [ a i 1 , a i 2 , ⋯ , a i n ] = k i [ a 11 , a 12 , ⋯ , a 1 n ] 则称矩阵 A 为一致矩阵 若矩阵 A= \left[ \begin{matrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}\\ \vdots&&\ddots\\ a_{n1}&&&a_{nn} \end{matrix} \right]满足: \\ \space\\ a_{ij}>0\\a_{11}=a_{22}=\cdots=a_{nn}=1\\ [a_{i1},a_{i2},\cdots,a_{in}] = k_i[a_{11},a_{12},\cdots,a_{1n}] \\则称矩阵 A 为一致矩阵 若矩阵A= a11a21⋮an1a12⋯⋱a1nann 满足: aij>0a11=a22=⋯=ann=1[ai1,ai2,⋯,ain]=ki[a11,a12,⋯,a1n]则称矩阵A为一致矩阵
由于涉及到的知识点过多,篇幅受限不做详细介绍与证明。
参考文献
[1] 汪应洛.系统工程[M].5版.北京:机械工业出版社,2015.12:123.
[2] David C. Lay,Steven R. Lay,Judi J. McDonald.线性代数及其应用[M].机械工业出版社:北京,2018.6:265.


![iOS “[App] if we're in the real pre-commit handler we can't actually add any new fences due](https://img-blog.csdn.net/20161028160636902?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)