lle算法c 语言,LLE（Locally Linear Embedding）算法

article/2025/10/14 5:29:27

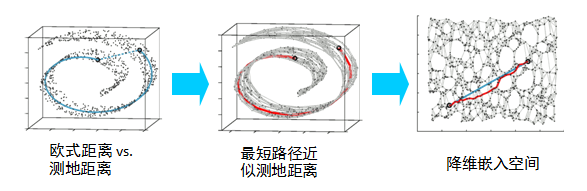
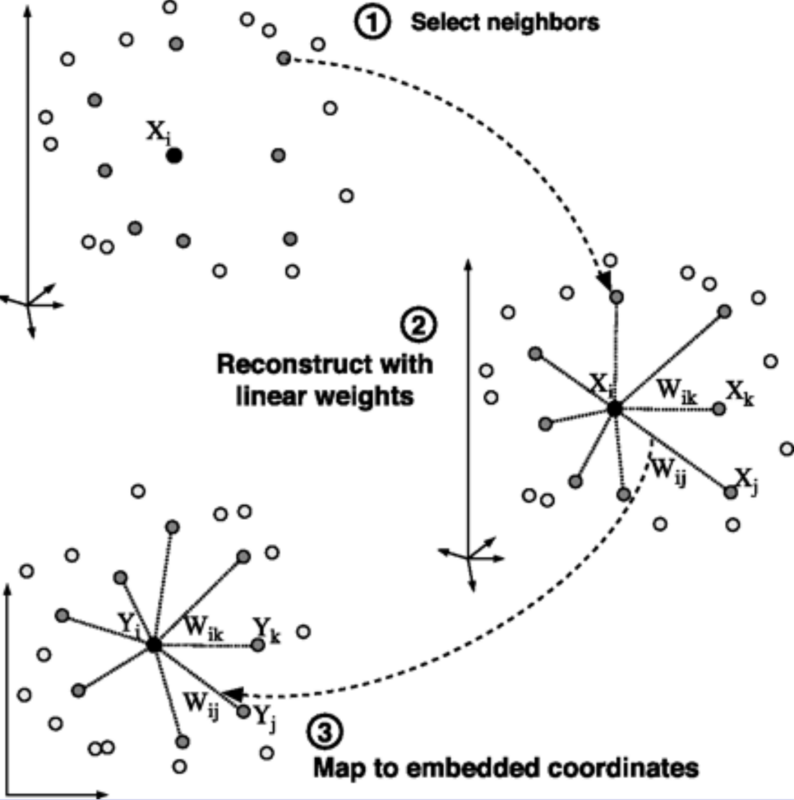
Core idea

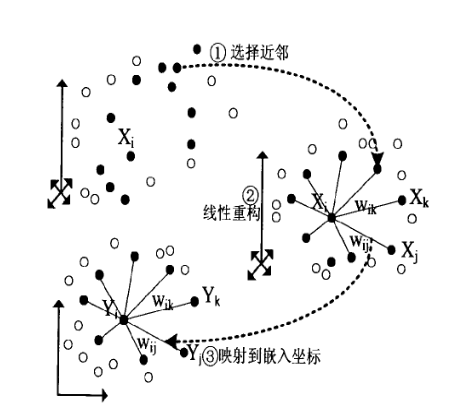
LLE is inherently a non-linear dimensionality reduction strategy

即局部线性嵌入算法。该算法是针对非线性信号特征矢量维数的优化方法，这种维数优化并不是仅仅在数量上简单的约简，而是在保持原始数据性质不变的情况下，将高维空间的信号映射到低维空间上，即特征值的二次提取。

Charateristics: neighborhood-preserving

Steps

Select neighbors

Reconstruct with linear weights

Map to embedded coordinates

ef6d4675a98e098b0272dbc4ae2e5c29.png

Basic formulas

ef067094bf5fb23d8c691f82e993cdf0.png

How to translate this problem to eigenvalue solution

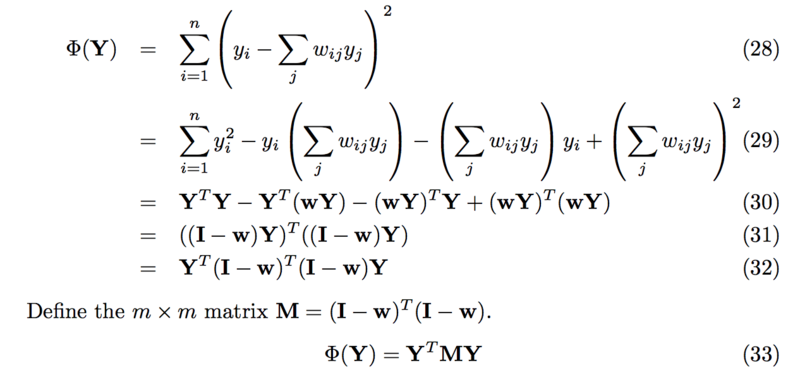
a695b8540f7b8009a7451774a4365f94.png

Use a Lagrange multiplier

Graph Embedding

寻找neighborhood：直接用Graph的邻接结构表示neighborhood

计算linear weights：直接用邻接矩阵W

生成embedding：计算矩阵M特征值，当节点数为n，embedding为q维时，取[n-q, n-1]的特征向量为embedding结果

Code

simple_code:

Python

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets, manifold

from mpl_toolkits.mplot3d import Axes3D

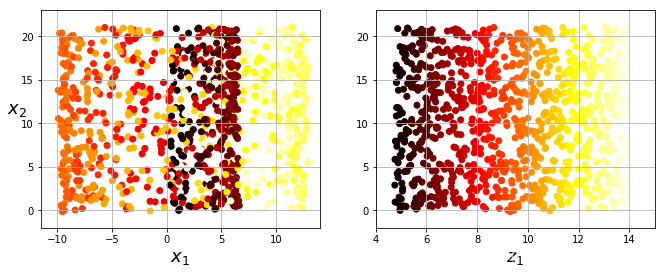
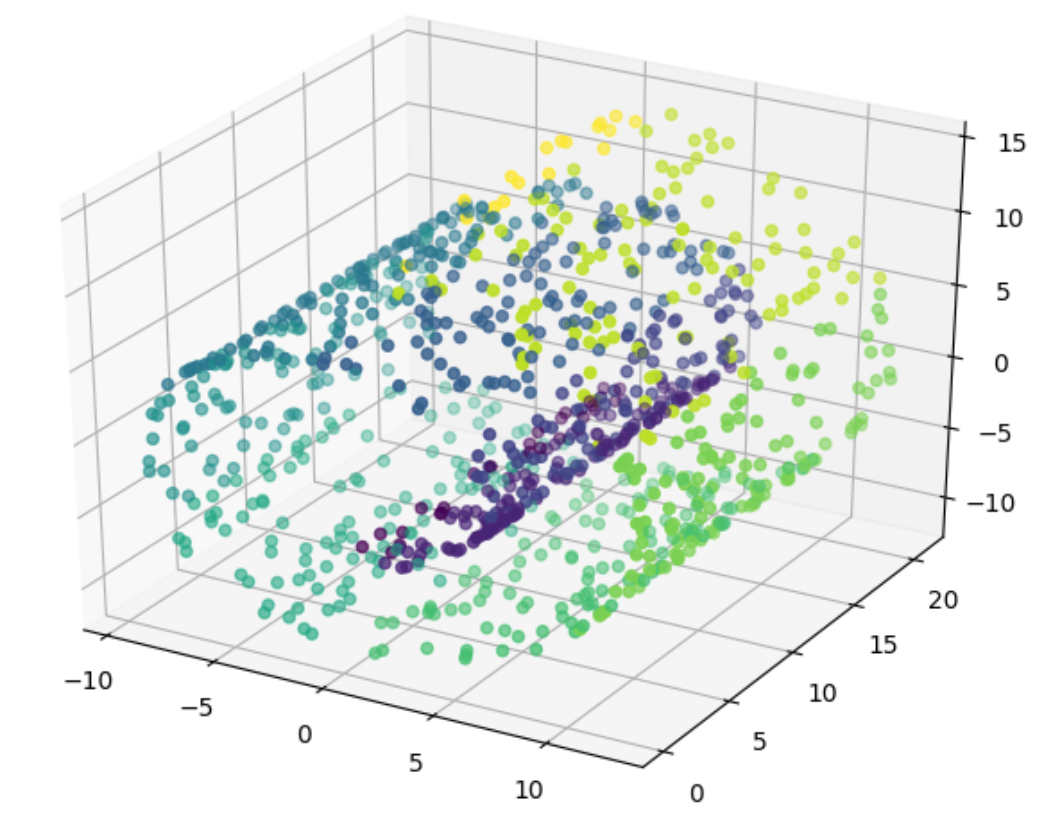
swiss_roll = datasets.make_swiss_roll(n_samples=1000)

X = swiss_roll[0]

Y = np.floor(swiss_roll[1])

d = 3

k = 999

fig_original = plt.figure('swiss_roll')

ax = Axes3D(fig_original)

ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=Y)

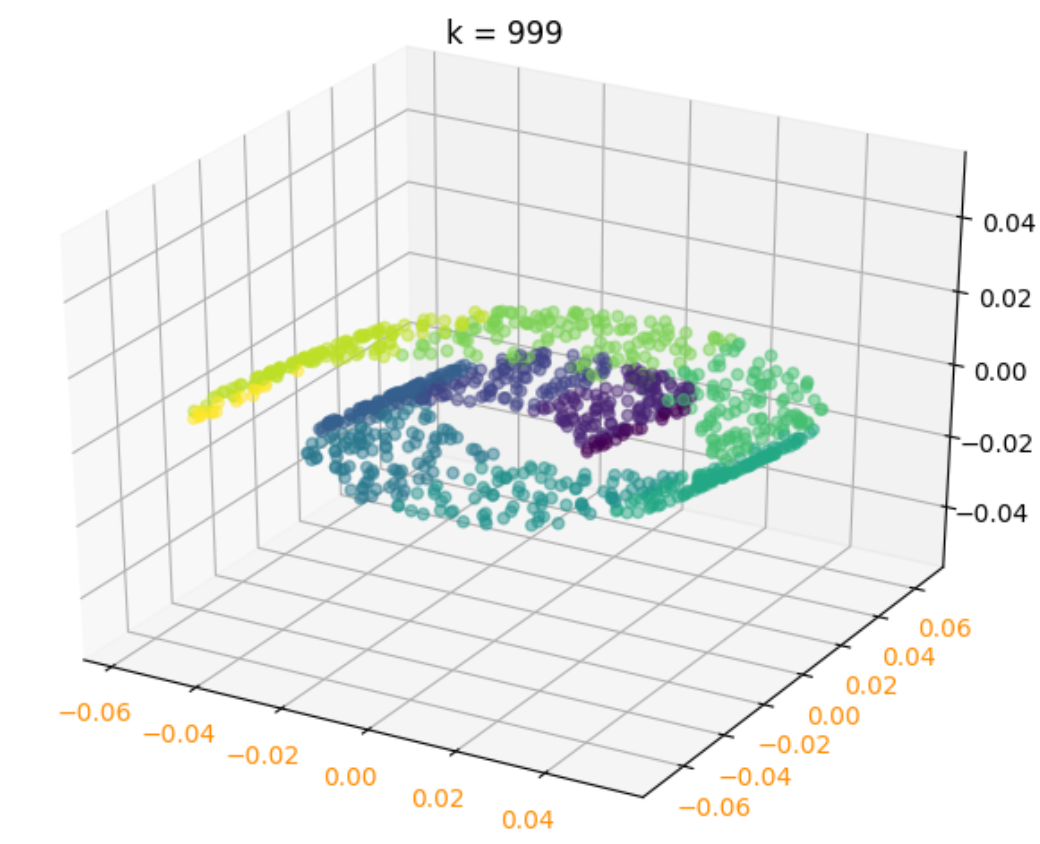
LLE = manifold.LocallyLinearEmbedding(n_components=d, n_neighbors=k, eigen_solver='auto')

X_r = LLE.fit_transform(X)

fig = plt.figure('LLE')

ax = Axes3D(fig)

ax.scatter(X_r[:, 0], X_r[:, 1], marker='o', c=Y, alpha=0.5)

ax.set_title("k = %d" % k)

plt.xticks(fontsize=10, color='darkorange')

plt.yticks(fontsize=10, color='darkorange')

plt.show()

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

importnumpyasnp

importmatplotlib.pyplotasplt

fromsklearnimportdatasets,manifold

frommpl_toolkits.mplot3dimportAxes3D

swiss_roll=datasets.make_swiss_roll(n_samples=1000)

X=swiss_roll[0]

Y=np.floor(swiss_roll[1])

d=3

k=999

fig_original=plt.figure('swiss_roll')

ax=Axes3D(fig_original)

ax.scatter(X[:,0],X[:,1],X[:,2],marker='o',c=Y)

LLE=manifold.LocallyLinearEmbedding(n_components=d,n_neighbors=k,eigen_solver='auto')

X_r=LLE.fit_transform(X)

fig=plt.figure('LLE')

ax=Axes3D(fig)

ax.scatter(X_r[:,0],X_r[:,1],marker='o',c=Y,alpha=0.5)

ax.set_title("k = %d"%k)

plt.xticks(fontsize=10,color='darkorange')

plt.yticks(fontsize=10,color='darkorange')

plt.show()

2f1c4f82e60b50b39b70797297fce627.png

e4b12ddded87fffd9aeb0013d0c97b2c.png

another version:

Python

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets, decomposition, manifold

from mpl_toolkits.mplot3d import Axes3D

def load_data():

'''

从sklearn中读取swiss_roll数据集

:return:

'''

swiss_roll = datasets.make_swiss_roll(n_samples=1000)

return swiss_roll[0], np.floor(swiss_roll[1])

def LLE_components(*data):

X, Y = data

for n in [3, 2, 1]: # 最终的降维目标

lle = manifold.LocallyLinearEmbedding(n_components=n) # sklearn的LLE方法

lle.fit(X)

print("n = %d 重建误差：" % n, lle.reconstruction_error_)

def LLE_neighbors(*data):

X, Y = data

Neighbors = [1, 2, 3, 4, 5, 15, 30, 100, Y.size - 1] # 可以选择的几个邻域值

fig = plt.figure("LLE", figsize=(9, 9))

for i, k in enumerate(Neighbors):

lle = manifold.LocallyLinearEmbedding(n_components=2, n_neighbors=k, eigen_solver='dense')

'''

eigen_solver：特征分解的方法。有‘arpack’和‘dense’两者算法选择。

当然也可以选择'auto'让scikit-learn自己选择一个合适的算法。

‘arpack’和‘dense’的主要区别是‘dense’一般适合于非稀疏的矩阵分解。

而‘arpack’虽然可以适应稀疏和非稀疏的矩阵分解，但在稀疏矩阵分解时会有更好算法速度。

当然由于它使用一些随机思想，所以它的解可能不稳定，一般需要多选几组随机种子来尝试。

'''

X_r = lle.fit_transform(X)

ax = fig.add_subplot(3, 3, i + 1)

ax.scatter(X_r[:, 0], X_r[:, 1], marker='o', c=Y, alpha=0.5)

ax.set_title("k = %d" % k)

plt.xticks(fontsize=10, color="darkorange")

plt.yticks(fontsize=10, color="darkorange")

plt.suptitle("LLE")

plt.show()

X, Y = load_data()

fig = plt.figure('data')

ax = Axes3D(fig)

ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=Y)

LLE_components(X, Y)

LLE_neighbors(X, Y)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

importnumpyasnp

importmatplotlib.pyplotasplt

fromsklearnimportdatasets,decomposition,manifold

frommpl_toolkits.mplot3dimportAxes3D

defload_data():

'''

从sklearn中读取swiss_roll数据集

:return:

'''

swiss_roll=datasets.make_swiss_roll(n_samples=1000)

returnswiss_roll[0],np.floor(swiss_roll[1])

defLLE_components(*data):

X,Y=data

fornin[3,2,1]:# 最终的降维目标

lle=manifold.LocallyLinearEmbedding(n_components=n)# sklearn的LLE方法

lle.fit(X)

print("n = %d 重建误差："%n,lle.reconstruction_error_)

defLLE_neighbors(*data):

X,Y=data

Neighbors=[1,2,3,4,5,15,30,100,Y.size-1]# 可以选择的几个邻域值

fig=plt.figure("LLE",figsize=(9,9))

fori,kinenumerate(Neighbors):

lle=manifold.LocallyLinearEmbedding(n_components=2,n_neighbors=k,eigen_solver='dense')

'''

eigen_solver：特征分解的方法。有‘arpack’和‘dense’两者算法选择。

当然也可以选择'auto'让scikit-learn自己选择一个合适的算法。

‘arpack’和‘dense’的主要区别是‘dense’一般适合于非稀疏的矩阵分解。

而‘arpack’虽然可以适应稀疏和非稀疏的矩阵分解，但在稀疏矩阵分解时会有更好算法速度。

当然由于它使用一些随机思想，所以它的解可能不稳定，一般需要多选几组随机种子来尝试。

'''

X_r=lle.fit_transform(X)

ax=fig.add_subplot(3,3,i+1)

ax.scatter(X_r[:,0],X_r[:,1],marker='o',c=Y,alpha=0.5)

ax.set_title("k = %d"%k)

plt.xticks(fontsize=10,color="darkorange")

plt.yticks(fontsize=10,color="darkorange")

plt.suptitle("LLE")

plt.show()

X,Y=load_data()

fig=plt.figure('data')

ax=Axes3D(fig)

ax.scatter(X[:,0],X[:,1],X[:,2],marker='o',c=Y)

LLE_components(X,Y)

LLE_neighbors(X,Y)


http://chatgpt.dhexx.cn/article/tcsnE56H.shtml

相关文章

（流形降维）局部线性嵌入 - LLE

（流形降维）局部线性嵌入 - LLE

文章目录 一，流形学习概述二，如何使用LLE进行数据降维1.参数说明2.官网示例 三，实例说明1.PCA与LLE降维的区别2.每个点的邻居数量对降维结果的影响 四，LLE总结 一，流形学习概述 更多关于LLE原理 参考：局部…
阅读更多...
机器学习（二）降维（PCA，kPCA，LLE）

机器学习（二）降维（PCA，kPCA，LLE）

写在前面 这是一个新的板块，用于记录作者机器学习的学习历程，同时分享自己的学习笔记给大家，希望这份笔记能帮助大家，同时也欢迎大家一起学习交流指正，我会尽量做到周更。如果有用的话请记得关注点赞收藏！&…
阅读更多...
数据分析-降维-PCA-LDA-LLE

数据分析-降维-PCA-LDA-LLE

目录 前言 矩阵分解法 主成分分析（PCA） 核PCA 非负矩阵分解（NMF） FactorAnalysis 独立主成分分析（ICA） 判别分析法（LDA） 基于流形学习的数据降维方法 LLE MDS MDS实现 t…
阅读更多...
对人脸数据集，采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维 ---模式识别课程设计

对人脸数据集，采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维 ---模式识别课程设计

对人脸数据集“Labeled Faces in the Wild”：sklearn.datasets.fetch_lfw_people，下载地址aka LFW:http://vis-www.cs.umass.edu/lfw/lfw-funneled.tgz， 采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维，比较基于SVM或决策树等分类器的…
阅读更多...
LLE算法实现与sklearn实现

LLE算法实现与sklearn实现

在pyhton的机器学习库sklearn中，LLE等降维算法可以直接调用，在本次大作业中，根据LLE的推导过程编写算法实现了LLE，与mainfold自带的LLE进行对比。由于后面的实验中都是直接调用LocallyLinearEmbedding，所以用大量篇幅介…
阅读更多...
一句话总结LLE（流形学习）

一句话总结LLE（流形学习）

一句话总结LLE（流形学习） 核心：用一个样本点的邻居的线性组合近似重构这个样本，将样本投影到低维空间中后依然保持这种线性组合关系。 局部线性嵌入（简称LLE）将高维数据投影到低维空间中，并保持…
阅读更多...
流行学习一LLE_机器学习

流行学习一LLE_机器学习

前言： 流行学习主要用于聚类，分类和回归算法,例如人脸识别（旋转不变性，光照不变性） 流行是几何中一个概念，它是高维空间中的几何结构，即高维空间中点构成的集合。 简单的理解为二维空间的曲线&a…
阅读更多...
lle算法c 语言,局部线性嵌入算法（LLE）与其Python实现-Go语言中文社区

lle算法c 语言,局部线性嵌入算法（LLE）与其Python实现-Go语言中文社区

PCA是至今为止运用最为广泛的数据降维算法，它通过最小化重构误差达到将高维数据映射到低维并同时保留数据中所存在的绝大部分信息。但是一般的PCA也有缺点，它只能实现线性降维。当然现在也有kernel PCA可以实现非线性降维，但我们今天介绍的是…
阅读更多...
LLE降维

LLE降维

LLE 是 Locally Linear embedding 直观是在样本点的高维空间相邻近的话，可以用低维的子空间描述。 基本原理分三步： （1） 找到邻居 neighbors .(可以使用多种方法，邻居K的数目选择影响很大) （2&#xff09…
阅读更多...
局部线性嵌入LLE

局部线性嵌入LLE

[1]https://www.cnblogs.com/pinard/p/6266408.html [2]Graph Embedding Techniques, Applications, and Performance: A Survey 主要参考和图片来源[1] LLE推导算法流程 局部线性嵌入(Locally Linear Embedding,LLE)，一种重要降维方法，与PCA、LDA相比…
阅读更多...
LLE降维算法

LLE降维算法

欢迎关注”生信修炼手册”! 流形分析作为非线性降维的一个分支，拥有多种算法，常见的算法列表如下 流形分析的要点在于降维之后，仍然保留流形中的某些几何属性。之前介绍的isomap保留了测地距离这一几何属性，由于考虑的是全局关系&…
阅读更多...
LLE算法

LLE算法

Locally linear embedding (LLE) (Sam T.Roweis and Lawrence K.Saul, 2000)以及Supervised locally linear embedding (SLLE) (Dick and Robert, 2002) 是最近提出的非线性降维方法，它能够使降维后的数据保持原有拓扑结构。 LLE算法可以有图1所示的一个例子来描述。…
阅读更多...
LLE原理总结

LLE原理总结

原文： https://www.cnblogs.com/pinard/p/6266408.html?utm_sourceitdadao&utm_mediumreferral 局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，…
阅读更多...
LLE原理及推导过程

LLE原理及推导过程

1.概述 所谓LLE（局部线性嵌入）即”Locally Linear Embedding”的降维算法，在处理所谓流形降维的时候，效果比PCA要好很多。 首先，所谓流形，我们脑海里最直观的印象就是Swiss roll,在吃它的时候喜欢把它整个摊开成一张饼再吃，其实这个过程就实现了对瑞士卷的降维操作…
阅读更多...
LLE理解

LLE理解

背景 局部线性嵌入(Locally Linear Embedding，以下简称LLE)是一种降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于…
阅读更多...
局部线性嵌入(LLE)原理总结

局部线性嵌入(LLE)原理总结

局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。下面我们就对…
阅读更多...
机器学习之：LLE （locally linear embedding） 局部线性嵌入降维算法

机器学习之：LLE （locally linear embedding） 局部线性嵌入降维算法

文章目录 LLE1. LLE 是什么2. LLE 的主要思想3. LLE 算法推导过程3.1 如何找到 k 个近邻3.2 找 x i x_i xi​ 与这 k 个近邻的线性关系3.3 x i x_i xi​ 与 k 个近邻点的线性关系求解过程3.3.1 奇异值分解3.3.1.1 特征值分解 （EVD）3.3.1.2 奇异值分解&…
阅读更多...
安装HAXM

安装HAXM

老师给的是在网上下载HAXM。但事实上打开这里你会发现Android 已经自动下载了HAXM 因此你要做的是找到HAXM路径，然后继续安装它。我的路径是 C:\Users\DELL\AppData\Local\Android\Sdk\extras\intel\Hardware_Accelerated_Execution_Manager
阅读更多...
Intel x86 Emulator Accelerator(HAXM installer)无法安装

Intel x86 Emulator Accelerator(HAXM installer)无法安装

在sdk manager中Intel x86 Emulator Accelerator(HAXM installer)后面显示 NOT compatible with windows 这个时候可以尝试手动安装Intel x86 Emulator Accelerator(HAXM installer) 1、在网上下载后，https://software.intel.com/en-us/articles/intel-hardware-a…
阅读更多...
haxm intel庐_Android Studio中Intel HAXM的那些坑

haxm intel庐_Android Studio中Intel HAXM的那些坑

最近用过两台电脑折腾Android Studio，都是windows的系统，不知道为什么连着踩了两个坑。 第一台我结束了qemu-system-i386.exe这个倒霉的进程 导致我开启模拟器的时候一直提示我没有安装Intel HAXM，没办法咯，只好再安装一遍&#x…
阅读更多...
推荐文章

Copyright @ 2022~2023