局部线性嵌入LLE

article/2025/10/14 5:58:53

[1]https://www.cnblogs.com/pinard/p/6266408.html
[2]Graph Embedding Techniques, Applications, and Performance: A Survey
主要参考和图片来源[1]

- LLE推导
- 算法流程

局部线性嵌入(Locally Linear Embedding,LLE)，一种重要降维方法，与PCA、LDA相比，更注重保持样本局部线性特征，常用语图像识别、高维数据可视化等。

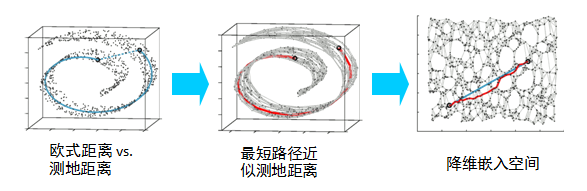
数学意义上的流形：一个不闭合曲面，曲面上数据分布均匀，特征比较稠密，流形降维就是把流形从高维到低维的降维过程，并在降维中保留流形高维的特征。
这里写图片描述

我的理解：数据分布于高维的一个曲面，流行学习就是将这个曲面降维展开表达出来

这里写图片描述

LLE
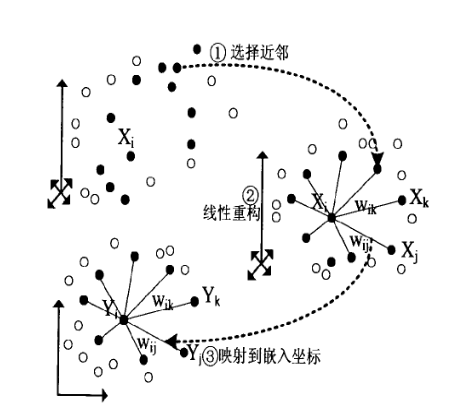
LLE假设数据在较小的局部是线性的，即样本 $x_1$ 可以由K个近邻样本 $x_2,x_3,x_4$ 线性表示

x 1 = w 12 x 2 + w 13 x 3 + w 14 x 4

$x_1=w_{12}x_2+w_{13}x_3+w_{14}x_4$
则希望降维之后依然保持这种线性关系

x' 1 \approx w 12 x' 2 + w 13 x' 3 + w 14 x' 4

$x_1' \approx w_{12}x_2'+w_{13}x_3'+w_{14}x_4'$
由于只考虑了局部线性关系，所以复杂度低很多

LLE推导

首先设定邻域大小k，然后寻找某个样本与近邻样本的线性关系，即权重系数。
假设有m个n维样本 $\{x_1,x_2,...,x_m\}$ ，则有损失函数

J (w) = \sum i = 1 m ‖ x i - \sum j = 1 k w i j x j ‖ 22

$J(w)=\sum_{i=1}^{m}\|x_i-\sum_{j=1}^{k}w_{ij}x_j\|^2_2$
对权重系数有归一化限制

\sum j = 1 k w i j = 1

$\sum_{j=1}^k w_{ij}=1$
对损失函数矩阵化

J (W) = \sum i = 1 m ‖ x i - \sum j = 1 k w i j x j ‖ 22 = \sum i = 1 m ‖ \sum j = 1 k w i j x i - \sum j = 1 k w i j x j ‖ 22 = \sum i = 1 m ‖ \sum j = 1 k w i j (x i - x j) ‖ 22 = \sum i = 1 m W T i (x i - x j) T (x i - x j) W i

$\begin{align*} J(W)&=\sum_{i=1}^{m} \|x_i-\sum_{j=1}^{k}w_{ij}x_j \|^2_2 \\ &=\sum_{i=1}^{m} \|\sum_{j=1}^{k} w_{ij}x_i -\sum_{j=1}^{k} w_{ij}x_j \|^2_2\\ &=\sum_{i=1}^{m}\|\sum_{j=1}^{k}w_{ij}(x_i-x_j) \|^2_2\\ &=\sum_{i=1}^{m} W_i^T (x_i-x_j)^T (x_i-x_j) W_i \end{align*}$

其中 $W_i=(w_{i1},w_{i2},...,w_{ik})^T$
表示局部协方差 $Z_i=(x_i-x_j)^T(x_i-x_j)$
则简化为

J (W) = \sum i = 1 m W T i Z i W i

$J(W)=\sum_{i=1}^{m} W_i^T Z_i W_i$
对约束有

\sum j = 1 k w i j = W T i 1 k = 1

$\sum_{j=1}^k w_{ij}=W_i^T 1_k=1$
其中1k为k维全1向量

则拉格朗日乘子法：

L (W) = \sum i = 1 m W T i Z i W i + λ (W T i 1 k - 1)

$L(W)=\sum_{i=1}^m W_i^T Z_i W_i +\lambda (W_i^T 1_k -1)$
对W求导取0得

2 Z i W i + λ 1 k = 0

$2Z_iW_i+\lambda 1_k=0$
则

W i = λ' Z - 1 i 1 k λ' = - 1 2 λ

$W_i=\lambda ' Z_i^{-1} 1_k\\ \lambda ' =-\frac{1}{2}\lambda$
利用约束做归一化有

W i = Z - 1 i 1 k 1 T k Z - 1 i 1 k

$W_i=\frac{Z_i^{-1} 1_k}{1_k^T Z_i^{-1} 1_k}$

注：把 $1_k^T挪到左边就对上了。。。$

至此，获得高维的权重系数，希望权重系数保持。设定n维样本集 $\{x_1,x_2,...,x_m\}$ 在低维的d维度投影为 $\{y_1,y_2,...,y_m\}$ ，希望保持线性关系且均方差损失函数最小，则最小化损失函数

$J (y) = \sum i = 1 m ‖ y i - \sum j = 1 k w i j y j ‖ 22$ $J(y)=\sum_{i=1}^{m} \|y_i-\sum_{j=1}^{k} w_{ij}y_j \|_2^2$
区别在于高维的时候是求权重系数W，低维时是求低位数据Y

为了得到标准化低维数据，加入约束条件

$\sum i = 1 m y i = 0; 1 m \sum i = 1 m y i y T i = I$ $\sum_{i=1}^{m} y_i=0;\frac{1}{m}\sum_{i=1}^{m} y_i y_i^T=I$

将目标损失函数矩阵化

J (Y) = \sum i = 1 m ‖ y i - \sum j = 1 k w i j y j ‖ 22 = \sum i = 1 m ‖ Y I i - Y W i ‖ 22 = t r (Y T (I - W) T (I - W) Y)

$\begin{align*} J(Y)&=\sum_{i=1}^{m} \|y_i - \sum_{j=1}^{k} w_{ij}y_j \|_2^2\\ &=\sum_{i=1}^{m} \|YI_i-YW_i \|_2^2\\ &=tr(Y^T (I-W)^T(I-W) Y) \end{align*}$
令