（流形降维）局部线性嵌入 - LLE

article/2025/10/14 5:33:41

文章目录

    • 一，流形学习概述
    • 二，如何使用LLE进行数据降维
      • 1.参数说明
      • 2.官网示例
    • 三，实例说明
      • 1.PCA与LLE降维的区别
      • 2.每个点的邻居数量对降维结果的影响
    • 四，LLE总结

一，流形学习概述

更多关于LLE原理 参考：局部线性嵌入(LLE)原理总结

LLE属于流形学习(Manifold Learning)的一种。因此我们首先看看什么是流形学习。流形学习是一大类基于流形的框架。数学意义上的流形比较抽象，不过我们可以认为LLE中的流形是一个不闭合的曲面。这个流形曲面有数据分布比较均匀，且比较稠密的特征，有点像流水的味道。基于流行的降维算法就是将流形从高维到低维的降维过程，在降维的过程中我们希望流形在高维的一些特征可以得到保留。

一个形象的流形降维过程如下图。我们有一块卷起来的布，我们希望将其展开到一个二维平面，我们希望展开后的布能够在局部保持布结构的特征，其实也就是将其展开的过程，就想两个人将其拉开一样。
　　　　在这里插入图片描述
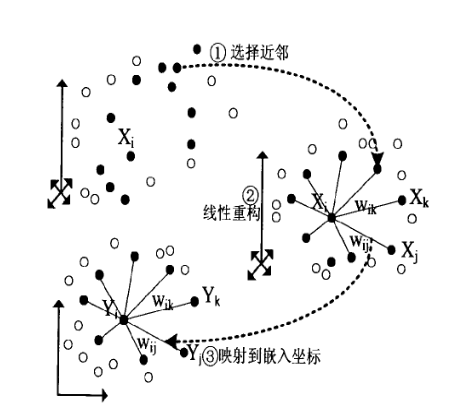
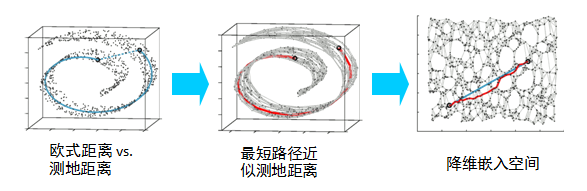
　　　　在局部保持布结构的特征，或者说数据特征的方法有很多种，不同的保持方法对应不同的流形算法。比如等距映射（ISOMAP）算法在降维后希望保持样本之间的测地距离而不是欧式距离，因为测地距离更能反映样本之间在流形中的真实距离。
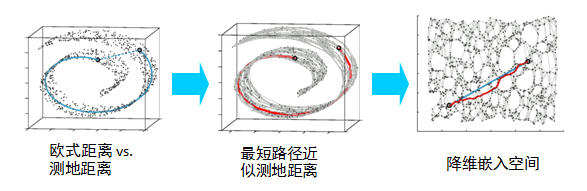
　　　　在这里插入图片描述
　　　　但是等距映射算法有一个问题就是他要找所有样本全局的最优解，当数据量很大，样本维度很高时，计算非常的耗时，鉴于这个问题，LLE通过放弃所有样本全局最优的降维，只是通过保证局部最优来降维。同时假设样本集在局部是满足线性关系的，进一步减少的降维的计算量。

二，如何使用LLE进行数据降维

官网：sklearn.manifold.LocallyLinearEmbedding

class sklearn.manifold.LocallyLinearEmbedding(*, n_neighbors=5, n_components=2, reg=0.001, eigen_solver='auto', tol=1e-06, max_iter=100, method='standard', hessian_tol=0.0001, modified_tol=1e-12, neighbors_algorithm='auto', random_state=None, n_jobs=None)

官网：sklearn.manifold.locally_linear_embedding

sklearn.manifold.locally_linear_embedding（X，*，n_neighbors，n_components，reg = 0.001，eigen_solver ='auto'，tol = 1e-06，max_iter = 100，method ='standard'，hessian_tol = 0.0001，modified_tol = 1e-12，random_state = None，n_jobs =无）

1.参数说明

Parameters
----------
n_neighbors：int每个点要考虑的邻居数量。n_components：int流形的坐标数。reg：float正则化常数乘以距离的局部协方差矩阵的轨迹。eigen_solver：str, {'auto', 'arpack', 'dense'}'auto' : 算法将尝试选择输入数据的最佳方法'arpack' : 在移位-反转模式下使用arnoldi迭代。对于此方法，M可以是稠密矩阵，稀疏矩阵或一般线性算子。警告：由于某些问题，ARPACK可能不稳定。最好尝试几个随机种子以检查结果。'dense' : 使用特征值的标准密集矩阵运算分解。对于此方法，M必须为数组或矩阵类型。对于大问题应避免使用此方法。tol: float, optional'arpack'方法的公差如果eigen_solver =='dense'不使用。max_iter：intarpack求解器的最大迭代次数。如果eigen_solver =='dense'，则不使用。method: str ('standard', 'hessian', 'modified' or 'ltsa')'standard' : 使用标准局部线性嵌入算法。'hessian': 使用Hessian eigenmap方法. 此方法要求n_neighbors > n_components * (1 + (n_components + 1) / 2 see reference [2]'modified': 使用修改后的局部线性嵌入算法。'ltsa': 使用局部切线空间对齐算法。hessian_tol: float, optional黑森州特征映射方法的公差。仅在以下情况下使用method == 'hessian'modified_tol: float, optional修正的LLE方法的公差。仅在以下情况下使用method == 'modified'neighbors_algorithm: str [‘auto’|’brute’|’kd_tree’|’ball_tree’]用于最近邻居搜索的算法，传递给邻居。NearestNeighbors实例random_state: int, RandomState instance, default=None当eigen_solver=='arpack' 时确定随机数生成器 。在多个函数调用之间传递int以获得可重复的结果。n_jobs: int or None, optional (default=None)要运行的并行作业数。 None除非joblib.parallel_backend上下文中，否则表示1 。 -1表示使用所有处理器。Attributes
----------
embedding_: array-like, shape [n_samples, n_components]存储嵌入向量
reconstruction_error_:float与重建相关的错误 embedding_nbrs_: NearestNeighbors object存储最近的邻居实例，包括BallTree或KDtree（如果适用）。Methods
-------
fit(self, X[, y])计算数据X的嵌入向量fit_transform(self, X[, y])		计算数据X的嵌入向量并变换X。get_params(self[, deep])获取此估计量的参数。set_params(self, \*\*params)设置此估算器的参数。transform(self, X)将新点转换为嵌入空间。

2.官网示例

>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import LocallyLinearEmbedding
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = LocallyLinearEmbedding(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)

三，实例说明

建立样本数为2000的生成瑞士卷曲线数据集

from sklearn.datasets import make_swiss_rollX, t = make_swiss_roll(n_samples=2000, noise=0.1)

3维数据集

X
>>>array([[ -8.5687585 ,   6.60327975,  -4.97423585],[ -6.01693799,   6.66425979,   6.19861014],[ -1.66603557,  15.1219713 ,   7.69390012],...,[ -4.17856203,  19.47152292,   7.34403002],[  4.03564557,  13.30477032,   5.9617141 ],[ -0.47941029,   4.95526013, -10.95709757]])

t
>>>array([ 9.9483257 ,  8.64246041,  8.0615649 , ...,  8.39105028,7.25609257, 10.95419387])

%matplotlib notebookfig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.Spectral,edgecolors='black')
plt.show()

在这里插入图片描述

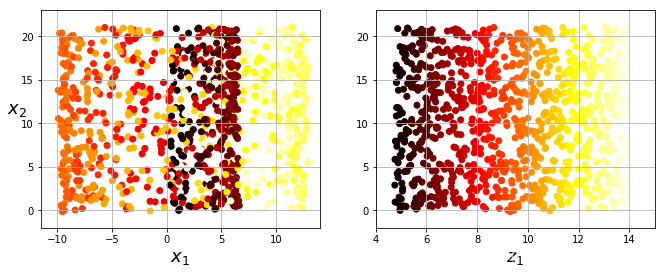
1.PCA与LLE降维的区别

首先使用PCA降至2维

pca = PCA(n_components=2)
pca.fit(X)
X_proj = pca.transform(X)
plt.scatter(X_proj[:,0],X_proj[:,1],s=50,c=t,cmap=plt.cm.Spectral,edgecolors='black')
plt.show()

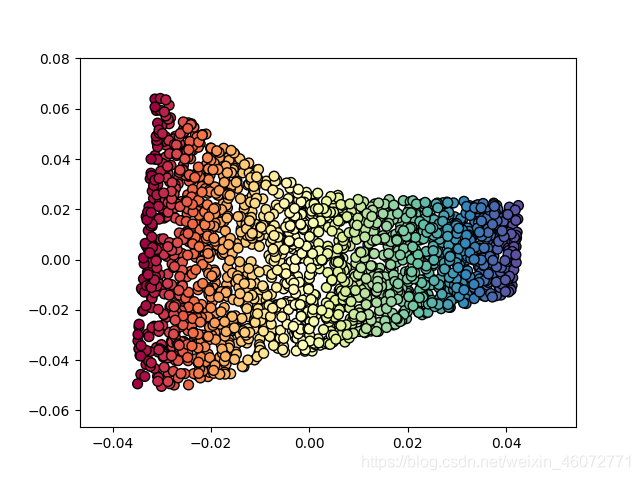
在这里插入图片描述
再使用LLE进行降维

X_r,err= LLE(X, n_neighbors=10, n_components=2)
plt.scatter(X_r[:,0],X_r[:,1],s=50,c=t,cmap=plt.cm.Spectral,edgecolors='black')
plt.show()

在这里插入图片描述

2.每个点的邻居数量对降维结果的影响

不同的参数 n_neighbors对将为结果的影响

fig,axes=plt.subplots(2,2)
nt = [4,8,12,16]X_r,err= LLE(X, n_neighbors=nt[0], n_components=2)
axes[0,0].scatter(X_r[:,0],X_r[:,1],s=10,c=t,cmap=plt.cm.Spectral,edgecolors='black')
X_r,err= LLE(X, n_neighbors=nt[1], n_components=2)
axes[0,1].scatter(X_r[:,0],X_r[:,1],s=10,c=t,cmap=plt.cm.Spectral,edgecolors='black')
X_r,err= LLE(X, n_neighbors=nt[2], n_components=2)
axes[1,0].scatter(X_r[:,0],X_r[:,1],s=10,c=t,cmap=plt.cm.Spectral,edgecolors='black')
X_r,err= LLE(X, n_neighbors=nt[3], n_components=2)
axes[1,1].scatter(X_r[:,0],X_r[:,1],s=10,c=t,cmap=plt.cm.Spectral,edgecolors='black')

在这里插入图片描述

四，LLE总结

LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。下面总结下LLE算法的优缺点。

LLE算法的主要优点有：

  • 可以学习任意维的局部线性的低维流形
  • 算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

LLE算法的主要缺点有

  • 算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。
  • 算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

http://chatgpt.dhexx.cn/article/sDvCWcBD.shtml

相关文章

机器学习（二）降维（PCA，kPCA，LLE）

机器学习（二）降维（PCA，kPCA，LLE）

写在前面 这是一个新的板块，用于记录作者机器学习的学习历程，同时分享自己的学习笔记给大家，希望这份笔记能帮助大家，同时也欢迎大家一起学习交流指正，我会尽量做到周更。如果有用的话请记得关注点赞收藏！&…
阅读更多...
数据分析-降维-PCA-LDA-LLE

数据分析-降维-PCA-LDA-LLE

目录 前言 矩阵分解法 主成分分析（PCA） 核PCA 非负矩阵分解（NMF） FactorAnalysis 独立主成分分析（ICA） 判别分析法（LDA） 基于流形学习的数据降维方法 LLE MDS MDS实现 t…
阅读更多...
对人脸数据集，采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维 ---模式识别课程设计

对人脸数据集，采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维 ---模式识别课程设计

对人脸数据集“Labeled Faces in the Wild”：sklearn.datasets.fetch_lfw_people，下载地址aka LFW:http://vis-www.cs.umass.edu/lfw/lfw-funneled.tgz， 采用PCA,KPCA,MDS,LLE,ISOMAPE五种方式降维，比较基于SVM或决策树等分类器的…
阅读更多...
LLE算法实现与sklearn实现

LLE算法实现与sklearn实现

在pyhton的机器学习库sklearn中，LLE等降维算法可以直接调用，在本次大作业中，根据LLE的推导过程编写算法实现了LLE，与mainfold自带的LLE进行对比。由于后面的实验中都是直接调用LocallyLinearEmbedding，所以用大量篇幅介…
阅读更多...
一句话总结LLE（流形学习）

一句话总结LLE（流形学习）

一句话总结LLE（流形学习） 核心：用一个样本点的邻居的线性组合近似重构这个样本，将样本投影到低维空间中后依然保持这种线性组合关系。 局部线性嵌入（简称LLE）将高维数据投影到低维空间中，并保持…
阅读更多...
流行学习一LLE_机器学习

流行学习一LLE_机器学习

前言： 流行学习主要用于聚类，分类和回归算法,例如人脸识别（旋转不变性，光照不变性） 流行是几何中一个概念，它是高维空间中的几何结构，即高维空间中点构成的集合。 简单的理解为二维空间的曲线&a…
阅读更多...
lle算法c 语言,局部线性嵌入算法（LLE）与其Python实现-Go语言中文社区

lle算法c 语言,局部线性嵌入算法（LLE）与其Python实现-Go语言中文社区

PCA是至今为止运用最为广泛的数据降维算法，它通过最小化重构误差达到将高维数据映射到低维并同时保留数据中所存在的绝大部分信息。但是一般的PCA也有缺点，它只能实现线性降维。当然现在也有kernel PCA可以实现非线性降维，但我们今天介绍的是…
阅读更多...
LLE降维

LLE降维

LLE 是 Locally Linear embedding 直观是在样本点的高维空间相邻近的话，可以用低维的子空间描述。 基本原理分三步： （1） 找到邻居 neighbors .(可以使用多种方法，邻居K的数目选择影响很大) （2&#xff09…
阅读更多...
局部线性嵌入LLE

局部线性嵌入LLE

[1]https://www.cnblogs.com/pinard/p/6266408.html [2]Graph Embedding Techniques, Applications, and Performance: A Survey 主要参考和图片来源[1] LLE推导算法流程 局部线性嵌入(Locally Linear Embedding,LLE)，一种重要降维方法，与PCA、LDA相比…
阅读更多...
LLE降维算法

LLE降维算法

欢迎关注”生信修炼手册”! 流形分析作为非线性降维的一个分支，拥有多种算法，常见的算法列表如下 流形分析的要点在于降维之后，仍然保留流形中的某些几何属性。之前介绍的isomap保留了测地距离这一几何属性，由于考虑的是全局关系&…
阅读更多...
LLE算法

LLE算法

Locally linear embedding (LLE) (Sam T.Roweis and Lawrence K.Saul, 2000)以及Supervised locally linear embedding (SLLE) (Dick and Robert, 2002) 是最近提出的非线性降维方法，它能够使降维后的数据保持原有拓扑结构。 LLE算法可以有图1所示的一个例子来描述。…
阅读更多...
LLE原理总结

LLE原理总结

原文： https://www.cnblogs.com/pinard/p/6266408.html?utm_sourceitdadao&utm_mediumreferral 局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，…
阅读更多...
LLE原理及推导过程

LLE原理及推导过程

1.概述 所谓LLE（局部线性嵌入）即”Locally Linear Embedding”的降维算法，在处理所谓流形降维的时候，效果比PCA要好很多。 首先，所谓流形，我们脑海里最直观的印象就是Swiss roll,在吃它的时候喜欢把它整个摊开成一张饼再吃，其实这个过程就实现了对瑞士卷的降维操作…
阅读更多...
LLE理解

LLE理解

背景 局部线性嵌入(Locally Linear Embedding，以下简称LLE)是一种降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于…
阅读更多...
局部线性嵌入(LLE)原理总结

局部线性嵌入(LLE)原理总结

局部线性嵌入(Locally Linear Embedding，以下简称LLE)也是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。下面我们就对…
阅读更多...
机器学习之：LLE （locally linear embedding） 局部线性嵌入降维算法

机器学习之：LLE （locally linear embedding） 局部线性嵌入降维算法

文章目录 LLE1. LLE 是什么2. LLE 的主要思想3. LLE 算法推导过程3.1 如何找到 k 个近邻3.2 找 x i x_i xi​ 与这 k 个近邻的线性关系3.3 x i x_i xi​ 与 k 个近邻点的线性关系求解过程3.3.1 奇异值分解3.3.1.1 特征值分解 （EVD）3.3.1.2 奇异值分解&…
阅读更多...
安装HAXM

安装HAXM

老师给的是在网上下载HAXM。但事实上打开这里你会发现Android 已经自动下载了HAXM 因此你要做的是找到HAXM路径，然后继续安装它。我的路径是 C:\Users\DELL\AppData\Local\Android\Sdk\extras\intel\Hardware_Accelerated_Execution_Manager
阅读更多...
Intel x86 Emulator Accelerator(HAXM installer)无法安装

Intel x86 Emulator Accelerator(HAXM installer)无法安装

在sdk manager中Intel x86 Emulator Accelerator(HAXM installer)后面显示 NOT compatible with windows 这个时候可以尝试手动安装Intel x86 Emulator Accelerator(HAXM installer) 1、在网上下载后，https://software.intel.com/en-us/articles/intel-hardware-a…
阅读更多...
haxm intel庐_Android Studio中Intel HAXM的那些坑

haxm intel庐_Android Studio中Intel HAXM的那些坑

最近用过两台电脑折腾Android Studio，都是windows的系统，不知道为什么连着踩了两个坑。 第一台我结束了qemu-system-i386.exe这个倒霉的进程 导致我开启模拟器的时候一直提示我没有安装Intel HAXM，没办法咯，只好再安装一遍&#x…
阅读更多...
AMD CPU无法安装Intel HAXM解决方法

AMD CPU无法安装Intel HAXM解决方法

步骤1. 步骤2. 找到安装目录（我的安装目录：D:\Android\SDK\extras\google\Android_Emulator_Hypervisor_Driver）下的这个文件：silent_install，右击该文件选择“以管理员运行”，即可。
阅读更多...
推荐文章

Copyright @ 2022~2023