写在前面
这是一个新的板块,用于记录作者机器学习的学习历程,同时分享自己的学习笔记给大家,希望这份笔记能帮助大家,同时也欢迎大家一起学习交流指正,我会尽量做到周更。如果有用的话请记得关注点赞收藏!!!
预告:下一章学习内容为无监督学习技术
1.思维导图
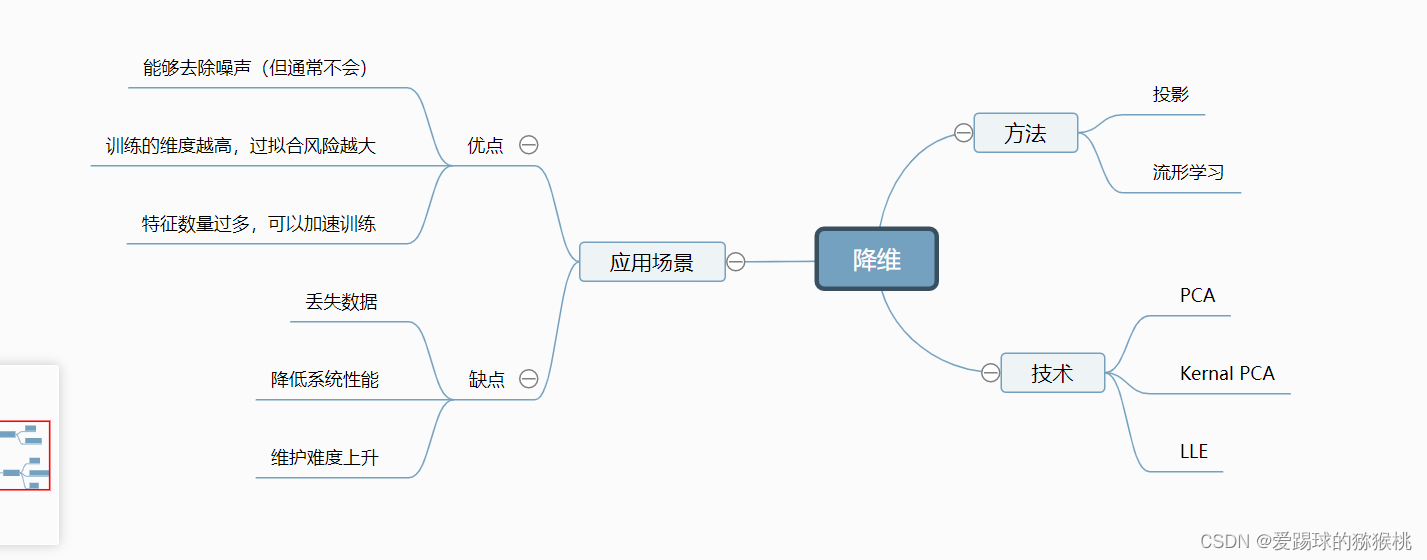
2.降维主要方法
降维能够加快训练速度,但不一定能使结果更好,取决于数据集和你的目的。
2.1投影和流形
投影是最简单的降维方法,即将所有训练实例垂直投影到子空间上,可以简单理解为把这个图形拍扁形成的图像,就像小学画三视图一样。
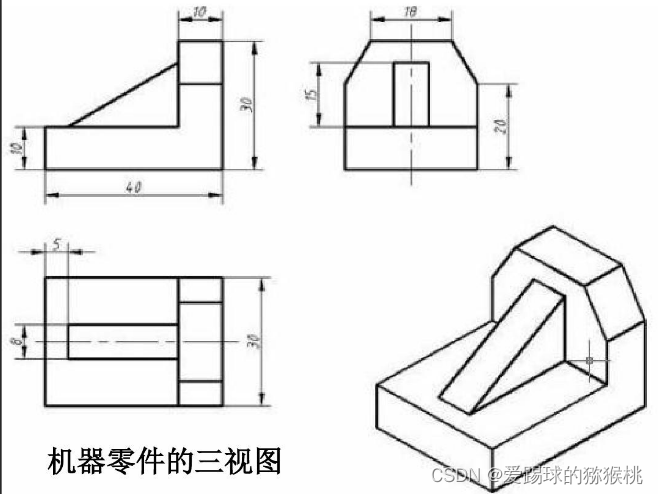
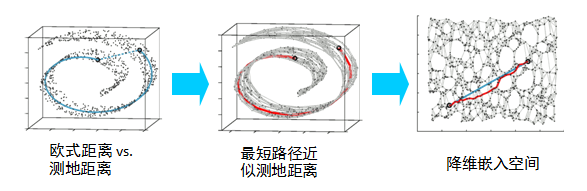
就像这样假设我们的数据分布就长成这个几何体一样,观察三视图,我们取其中任何一张图片(2D)都是不能很好的还原这个几何图形(3D)的,也就是说多数情况下子空间会发生旋转和扭动,并不能很好的反映数据本身的联系。比如说我们现在需要计算该几何体上两点之间的距离,如果利用投影,可能误差会非常大,而合理的计算方式是展开图形再测量,那么这样把三维的图形展开转为二维的形状就是流形。
2.2流型学习
流型学习是什么?什么时候使用呢?
我们通过对训练实例所在二维流形来进行建模,这就称为流形学习。这种方法假设高维数据集都接近于低维流形,同时如果使用了流形的低维空间来表示,那么分类和回归任务会变得更加简单。如果 数据集满足此假设 那么流形学习就是适用的。
3.三种常用降维技术
3.1 PCA(主成分分析)
主成分分析是目前最流形的降维算法,他识别最靠近数据的超平面然后将数据投影到其上面。
通常原始特征包含明显的冗余信息,主成分是通过确保特征之间没有信息重叠来尽可能有效的表示数据及其差异的特征组合。
主成分分析主要有以下步骤
3.1.1 选择主要成分
假设我们有一个二维数据集(寻找轴的数量等于数据集维度),那么我们需要找两条轴来表示,那么怎么选取呢,取决于哪条轴对差异性贡献度最高,也就是更加能还原该数据集。这里不做过多赘述(简单来说就是通过寻找不同方向的组合看看哪一个的和原始数据均方差比较小,即保留最大差异性)如该图所示,我们最后得到 c1代表第一个主要成分,c2代表第二个主要成分。
3.1.2 投影到d维度
选择好主要成分后,投影到该平面上就好
3.1.3 使用skLearn来完成PCA
from sklearn.decomposition import PCA pca=PCA(n_componets=2)##选择想要降维到哪个维度 result=pca.fit_transform(X)
3.1.4 手动PCA
这一步敲重点!!! 如果不使用sklearn的话记得要中心化一下
skLearn会帮助我们自动处理中心化,为什么要中心化?去看这个文章就好http://t.csdn.cn/F0zR2
X_centered=X-X.mean(axis=0)#中心化 U,s,Vt=np.linalg.svd(X_centered)#奇异值分解,找出主要成分 c1=Vt.T[:,0] #由于是二维,所以提取前两个主要成分(几维就几个),这是第一个 c2=Vt.T[:,1] #这是第二个 w2=Vt.T[:,:2] #两个主要成分 result=X_centered.dot(w2)#投影
3.1.5 一些比较有用的有关PCA东东
3.1.5.1 可解释方差比
每个主成分的可解释方差比,该比率表示沿着每个主成分的数据集方差的比率。可帮助我们知道这个主成分对于差异性贡献度是怎么样的
展示一下
pca.explained_variance_ratio_ ##输出array([0.8236738,0.1467383])可以看到第一个PC贡献了84.2%,第二个14%,所以最后一个PC贡献的挺少的
3.1.5.2 选择正确的维度
这里要分情况说,如果你是为了数据可视化那肯定最好三维或以下,但是如果你是为了用来处理数据分析,那最好是选可解释方差加起来最大的,这样你保留的差异性最大。
##一种方法是你直接在设置维度那里改成你要的比率就好 pca=PCA(n_components=0.95) ##还有一种手动 pca=PCA() pca.fit(x_train) cumsum=np.cumsum(pca.explained_variance_ratio_)#把可解释方差加起来 d=np.argmax(cumsum>=0.95)+1#选可解释方差和大于0.95的维度 pca=PCA(n_components=d)#设置维度
3.1.6 PCA其他方法
3.1.6.1 PCA压缩
这个的作用很简单就是减少
这个比较简单直接看代码,其实就是压缩(降维)和解压缩(升维)的转换,从而达到丢弃方差的目的
pca=PCA(n_components=0.95) #保留百分之95的方差 x_reduced=pca.fit(X_train) #训练得到(压缩) result=pca.inverse_transform(x_reduced) #把它转换原来的维度(解压缩)
这样我们得到的结果就是保留95%方差后的结果(即丢弃了5%的方差),这里有个概念,原始数据与重构数据之间的均方距离称为重构误差,其实这个方法还是非常实用的,在我们需要提取重要特征时可以使用,可以做到保留重要特征,消除部分噪声或者是加快训练速度(主要是这个)的目的。
3.1.6.2 增量PCA
对于大型数据集和在线学习来说增量PCA是很有用的,代码如下:
from sklearn.decomposition import IncrementalPCA n_batches=100 #把你数据分成几份 inc_pca=IncrementalPCA(n_components=d) #d=你想要的维度或者方差 for X_batch in np.array_split(X_train,n_batches):inc_pca.partial_fit(X_batch) #这里肯定是用partial——fit的,能保留参数继续学习 X_reduced=inc_pca.transform(X_train)
3.2 内核PCA(kPCA)
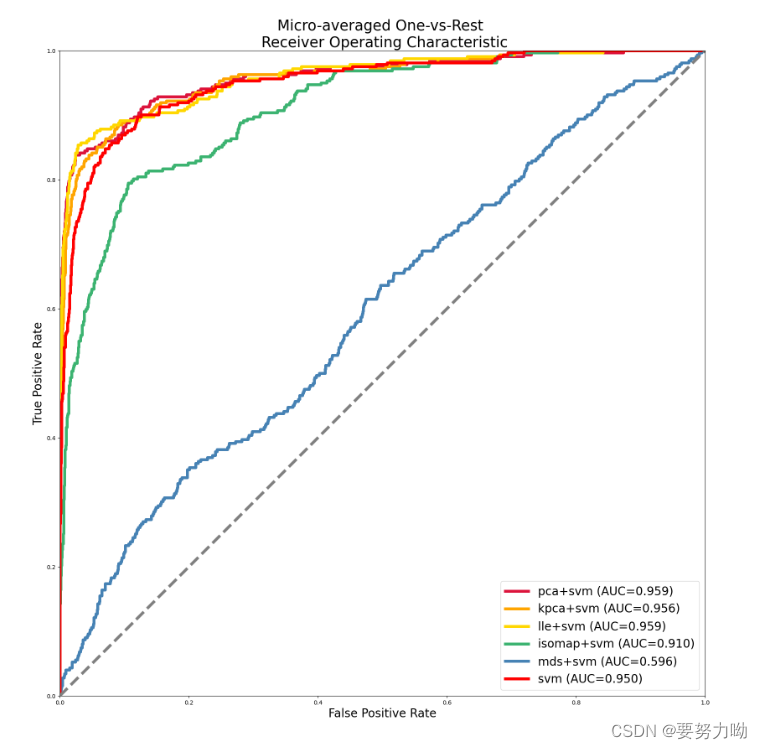
利用内核来执行复杂的非线性投影来降低维度,主要有两种rbf和sigmoid,这种方法比较擅长在投影后保留实例的聚类,但是一般没办法直接找出适合的参数和内核,所以就需要网格寻优一下。
这里给出一个用于逻辑回归分类之前降维的例子
代码如下
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticReression #用这个决定这个特征留不留(0/1)
from sklearn.pipeline import Pipeline
clf=Pipeline([
("kpca",KernelPCA(n_components=2)),
])
param_grid=[{
"kpca_gamma":np.linspace(0.03,0.05,10),
"kpca_kernel":["rbf","sigmoid"]
}]
grid_search=GridSearchCV(clf,param_grid,cv=3)
grid_search.fit(X,y)
print(grid_search.best_params_)#这个可以得到最佳内核和参数(得到最高分类准确率的)
还有一种思路是得到最小重构误差的(如果你想压缩的)把之前那个pca压缩的改改就行,代码差不多,可以把上面代码的网格寻优套上来,这里敲重点,KernelPCA里面fit_inverse_transform是关闭的,记得设置为True
from sklearn.metrics ipmort mean_squared_error pca=KernelPCA(n_components=0.95,kernel="rbf",gamma=0.0433,fit_inverse_transform=True) x_reduced=pca.fit(X_train) result=pca.inverse_transform(x_reduced) mean_squared_error(X_train,result)
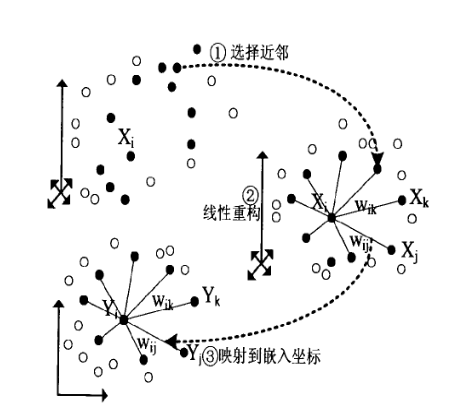
3.3 LLE(局部线性嵌入)
一种流形学习技术,跟投影没关系。特别适合展开扭曲的流形,尤其是没有太多噪声的情况下。
原理看这篇http://t.csdn.cn/klMG3,写的超好的大佬。