Locally linear embedding (LLE) (Sam T.Roweis and Lawrence K.Saul, 2000)以及Supervised locally linear embedding (SLLE) (Dick and Robert, 2002) 是最近提出的非线性降维方法，它能够使降维后的数据保持原有拓扑结构。
LLE算法可以有图1所示的一个例子来描述。在图1所示中，LLE能成功地将三维非线性数据映射到二维空间中。如果把图1（B）中红颜色和蓝颜色的数据分别看成是分布在三维空间中的两类数据，通过LLE算法降维后，则数据在二维空间中仍能保持相对独立的两类。在图1（B）中的黑色小圈中可以看出，如果将黑色小圈中的数据映射到二维空间中，如图1（C）中的黑色小圈所示，映射后的数据任能保持原有的数据流形，这说明LLE算法确实能保持流形的领域不变性。由此LLE算法可以应用于样本的聚类。而线性方法，如PCA和MDS，都不能与它比拟的。LLE算法操作简单，且算法中的优化不涉及到局部最小化。该算法能解决非线性映射，但是，当处理数据的维数过大，数量过多，涉及到的稀疏矩阵过大，不易于处理。在图1中的球形面中，当缺少北极面时，应用LLE算法则能很好的将其映射到二维空间中，如图1中的C所示。如果数据分布在整个封闭的球面上，LLE则不能将它映射到二维空间，且不能保持原有的数据流形。那么我们在处理数据中，首先假设数据不是分布在闭合的球面或者椭球面上。
图1 非线性降维实例：B是从A中提取的样本点（三维），通过非线性降维
算法（LLE），将数据映射到二维空间中（C）。从C图中的颜色可以看出
通过LLE算法处理后的数据，能很好的保持原有数据的邻域特性
LLE算法是最近提出的针对非线性数据的一种新的降维方法，处理后的低维数据均能够保持原有的拓扑关系。它已经广泛应用于图像数据的分类与聚类、文字识别、多维数据的可视化、以及生物信息学等领域中。
1 LLE算法
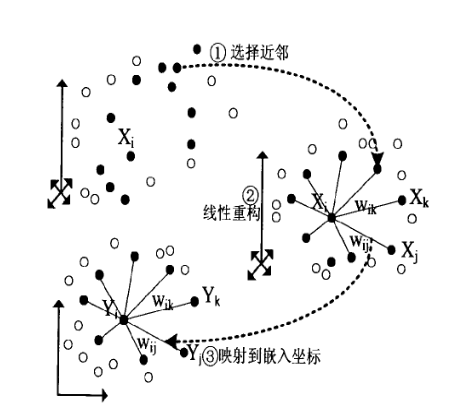
LLE算法可以归结为三步:(1)寻找每个样本点的k个近邻点；（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；（3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。具体的算法流程如图2所示。
图2 LLE算法流程
算法的第一步是计算出每个样本点的k个近邻点。把相对于所求样本点距离最近的k个样本点规定为所求样本点的 个近邻点。k是一个预先给定值。Sam T.Roweis 和 Lawrence K.Saul算法采用的是欧氏距离，则减轻复杂的计算。然而本文是假定高维空间中的数据是非线性分布的，采用了diijstra距离。Dijkstra 距离是一种测地距离，它能够保持样本点之间的曲面特性，在ISOMAP算法中有广泛的应用。针对样本点多的情况，普通的dijkstra算法不能满足LLE算法的要求。
LLE算法的第二步是计算出样本点的局部重建权值矩阵。这里定义一个误差函数，如下所示：
其中
为
的k个近邻点，
是 与
之间的权值，且要满足条件：
。这里求取W矩阵，需要构造一个局部协方差矩阵 
。
将上式与
相结合，并采用拉格朗日乘子法，即可求出局部最优化重建权值矩阵：
在实际运算中，可能是一个奇异矩阵，此时必须正则化，如下所示：
其中r是正则化参数，I是一个kxk的单位矩阵。
LLE算法的最后一步是将所有的样本点映射到低维空间中。映射条件满足如下所示：
其中，
为损失函数值，
是的输出向量，
是的k个近邻点，且要满足两个条件，即：
其中I是
的单位矩阵。这里的
可以存储在
的稀疏矩阵W中，当
是的近邻点时，
，否则，
。则损失函数可重写为：
其中M是一个的对称矩阵,其表达式为:
要使损失函数值达到最小, 则取Y为M的最小m个非零特征值所对应的特征向量。在处理过程中，将M的特征值从小到大排列，第一个特征值几乎接近于零，那么舍去第一个特征值。通常取第
间的特征值所对应的特征向量作为输出结果。
![]()
![]()
代码：
Matlab LLE主函数：
- % LLE ALGORITHM (using K nearest neighbors)
- % [Y] = lle(X,K,dmax)
- % X ：data as D x N matrix (D = dimensionality, N = #points)
- % K ：number of neighbors
- % dmax ：max embedding dimensionality
- % Y ：embedding as dmax x N matrix
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- function [Y] = lle(X,K,d)
- [D,N] = size(X);
- fprintf(1,'LLE running on %d points in %d dimensions\n',N,D);
-
- %% Step1: compute pairwise distances & find neighbour
- fprintf(1,'-->Finding %d nearest neighbours.\n',K);
- X2 = sum(X.^2,1);
- distance = repmat(X2,N,1)+repmat(X2',1,N)-2*X'*X;
- [sorted,index] = sort(distance);
- neighborhood = index(2:(1+K),:);
-
- % Step2: solve for recinstruction weights
- fprintf(1,'-->Solving for reconstruction weights.\n');
- if(K>D)
- fprintf(1,' [note: K>D; regularization will be used]\n');
- tol=1e-3; % regularlizer in case constrained fits are ill conditioned
- else
- tol=0;
- end
-
- W = zeros(K,N);
- for ii=1:N
- z = X(:,neighborhood(:,ii))-repmat(X(:,ii),1,K); % shift ith pt to origin
- C = z'*z; % local covariance
- C = C + eye(K,K)*tol*trace(C); % regularlization (K>D)
- W(:,ii) = C\ones(K,1); % solve Cw=1
- W(:,ii) = W(:,ii)/sum(W(:,ii)); % enforce sum(w)=1
- end;
-
- % Step 3: compute embedding from eigenvects of cost matrix M=(I-W)'(I-W)
- fprintf(1,'-->Computing embedding.\n');
- % M=eye(N,N); % use a sparse matrix with storage for 4KN nonzero elements
- M = sparse(1:N,1:N,ones(1,N),N,N,4*K*N);
- for ii=1:N
- w = W(:,ii);
- jj = neighborhood(:,ii);
- M(ii,jj) = M(ii,jj) - w';
- M(jj,ii) = M(jj,ii) - w;
- M(jj,jj) = M(jj,jj) + w*w';
- end;
-
- % calculation of embedding
- options.disp = 0;
- options.isreal = 1;
- options.issym = 1;
- [Y,eigenvals] = eigs(M,d+1,0,options);
- Y = Y(:,2:d+1)'*sqrt(N); % bottom evect is [1,1,1,1...] with eval 0
- fprintf(1,'Done.\n');
-
- %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
- % other possible regularizers for K>D
- % C = C + tol*diag(diag(C)); % regularlization
- % C = C + eye(K,K)*tol*trace(C)*K; % regularlization
