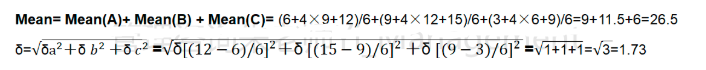三点估算法主要来自于项目的计划评审技术 PERT,能评估时间与概率的关系。
三点估算法不仅可以用于定量风险分析,也可用于进度管理中活动历时估算。
先记住几个概念:
最乐观时间TO:完成该工作最少需要的时间;
最悲观时间TP:完成该工作最多需要的时间;
最可能时间TM:完成该工作最可能需要的时间;
标准差可以理解为满足正态分布的最小单位;
方差可以理解为标准差的平方;
公式是这样的:
期望时间=(最乐观TO+4*最可能TM+最悲观TP)/6
标准差=(最悲观-最乐观)/6
方差=标准差²
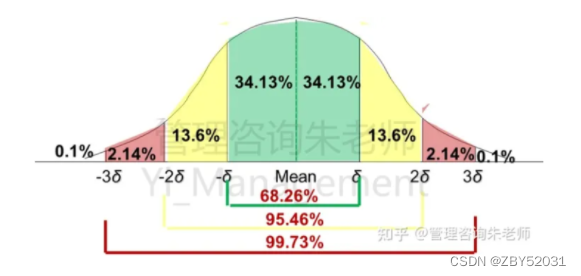
正态分布图: