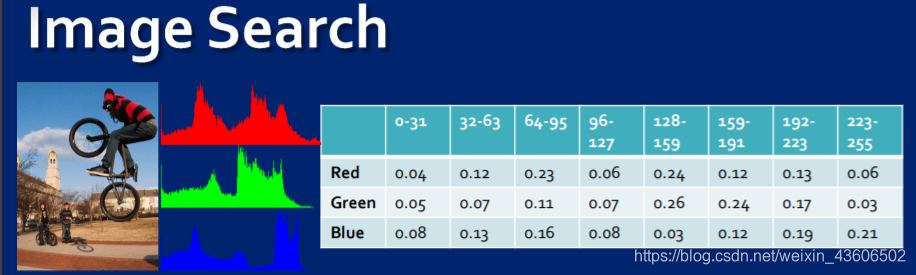
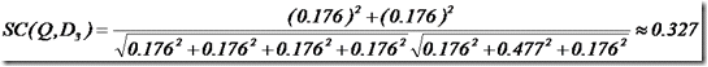定义：AppScan是IBM的一款web安全扫描工具，主要适用于Windows系统。该软件内置强大的扫描引擎，可以测试和评估Web服务和应用程序的风险检查，根据网站入口自动对网页链接进行安全扫描，扫描之后会提供扫描报告和修复建议等。

工作原理：爬行-通过搜索（爬行）发现整个 Web 应用结构；验证-通过对于 Respone 的分析验证是否存在安全漏洞；分析-根据分析，发送修改的 HTTP Request 进行攻击尝试（扫描规则库）

安装版本选择，建议安装最新版本，部分版本会对电脑的要求会高一些，可能会出现不适配的情况，有IBM证书和HCL证书两种形式，两种形式对应不同的版本，如果下载的是需要导入IBM证书的版本，需要找到IBM的证书进行导入，若是HCL的，则需要找到HCL的进行导入，不同的版本，破解的方式是不同的，需要注意

实操：

对无需登录的系统，进行浏览器扫描测试，可以看到仪表板清晰的展示了需要解决的问题，以及问题的严重等级程度

 

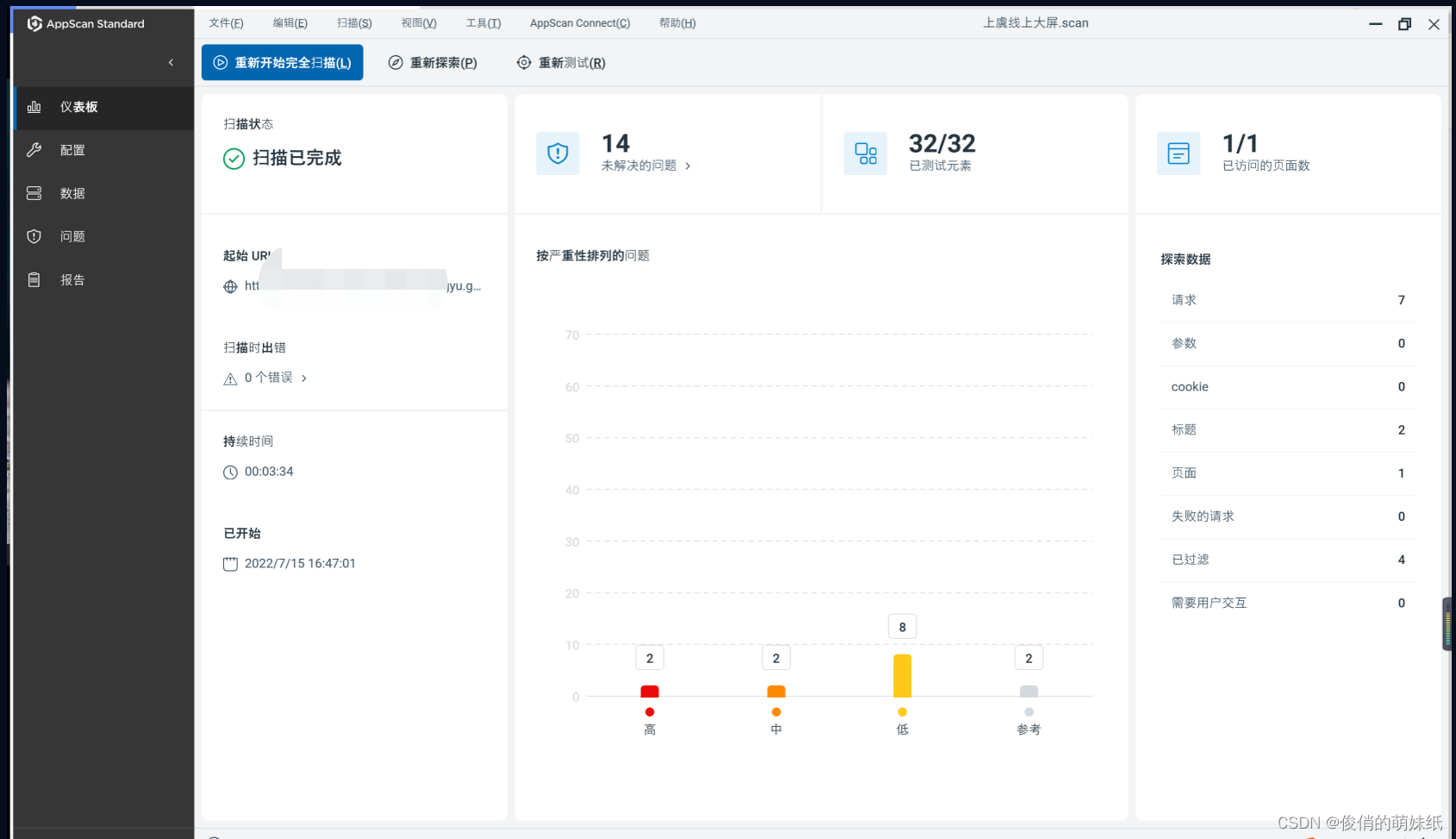
如高级问题，修改api接口的路径，响应结果是200，说明这个接口是能访问通畅的，会造成什么后果，对方可能通过这个接口，无限的访问，增加服务器负荷，可能会导致系统瘫痪

 

 

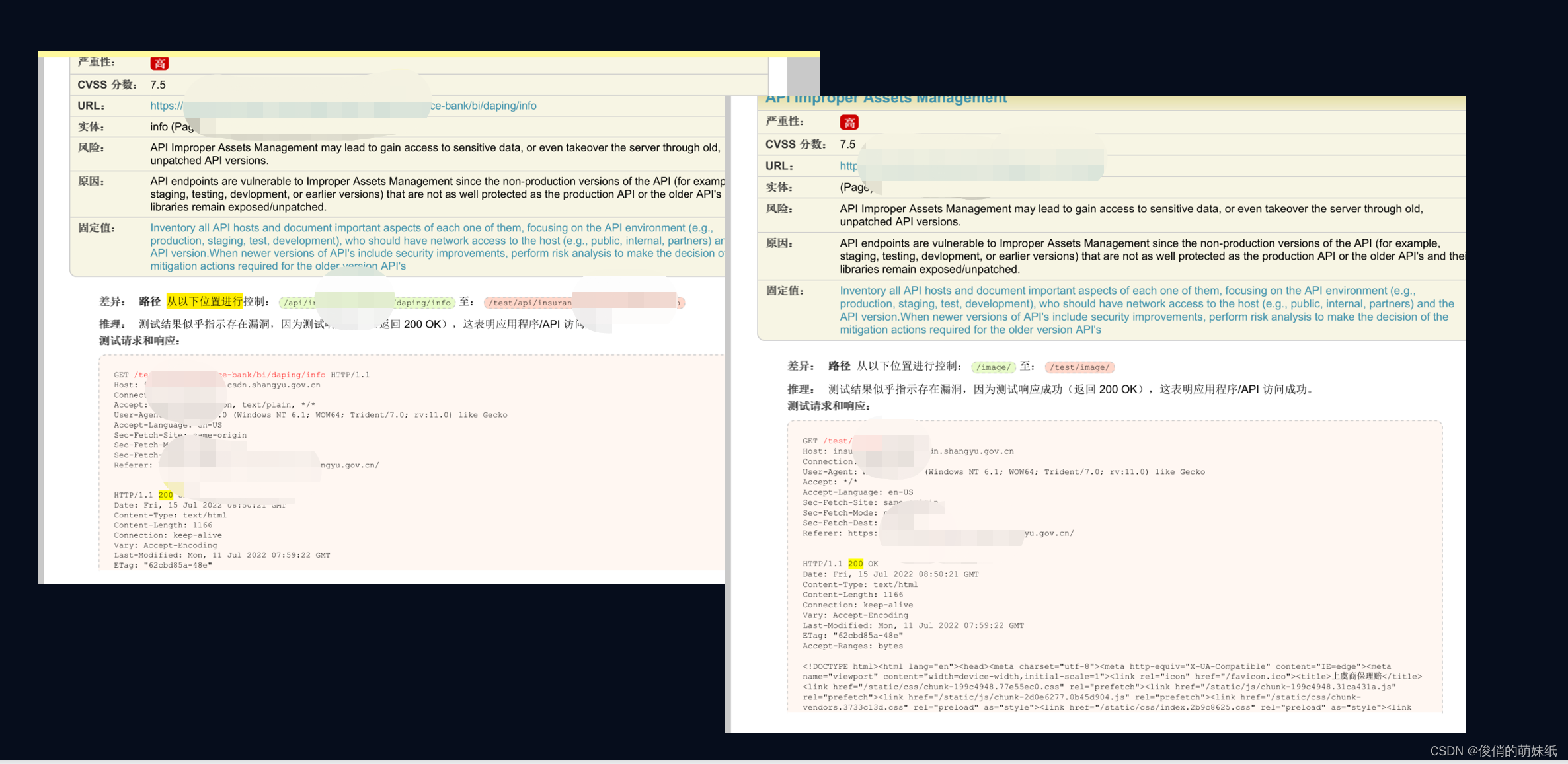
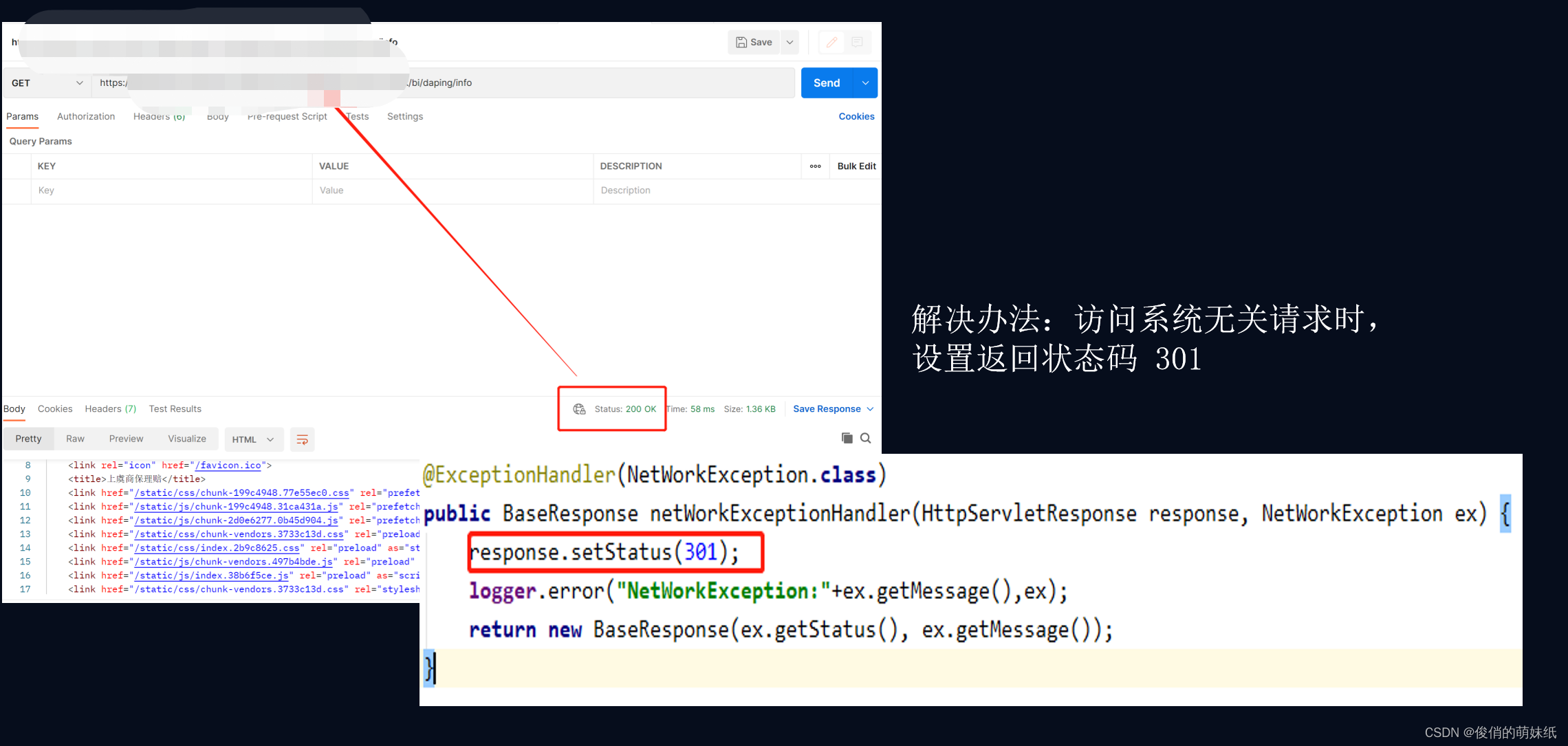
 可以通过什么方式解决该问题呢？开发可在代码中进行设置，除了正确的状态码之外的api请求，返回一个统一的状态码即可

 

 

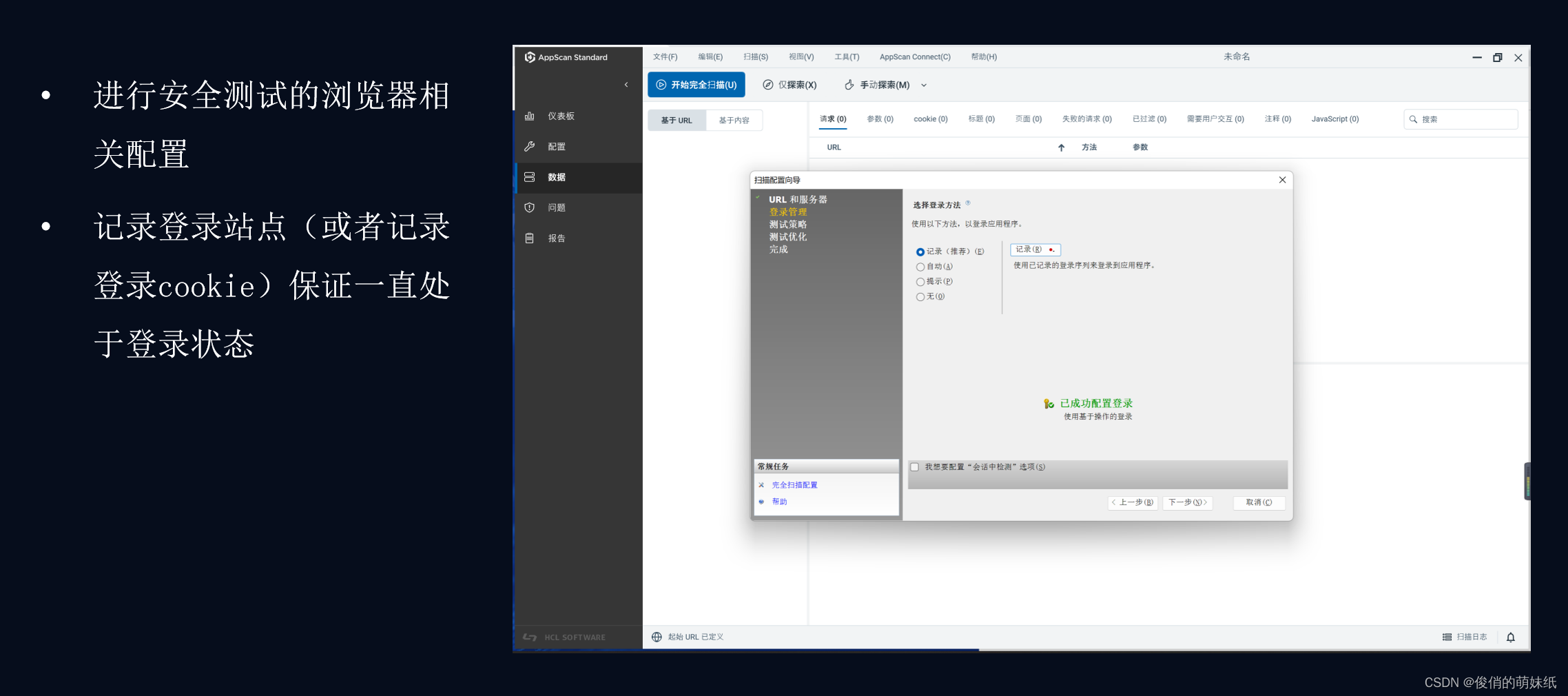
带登录页面的系统进行浏览器安全测试扫描：

1、配置浏览器参数

2、记录登录参数的cookie数据，记录登录状态，保持登录态

3、配置测试策略

4、设置完成后，进行相关安全扫描

比如扫描的结果中修改的请求方式：原来请求方式是post被修改为了Delet类型，但是请求响应是OK 200，那说明url链接是存在一定风险的

解决方式，通过修改返回状态码，即可解决

 

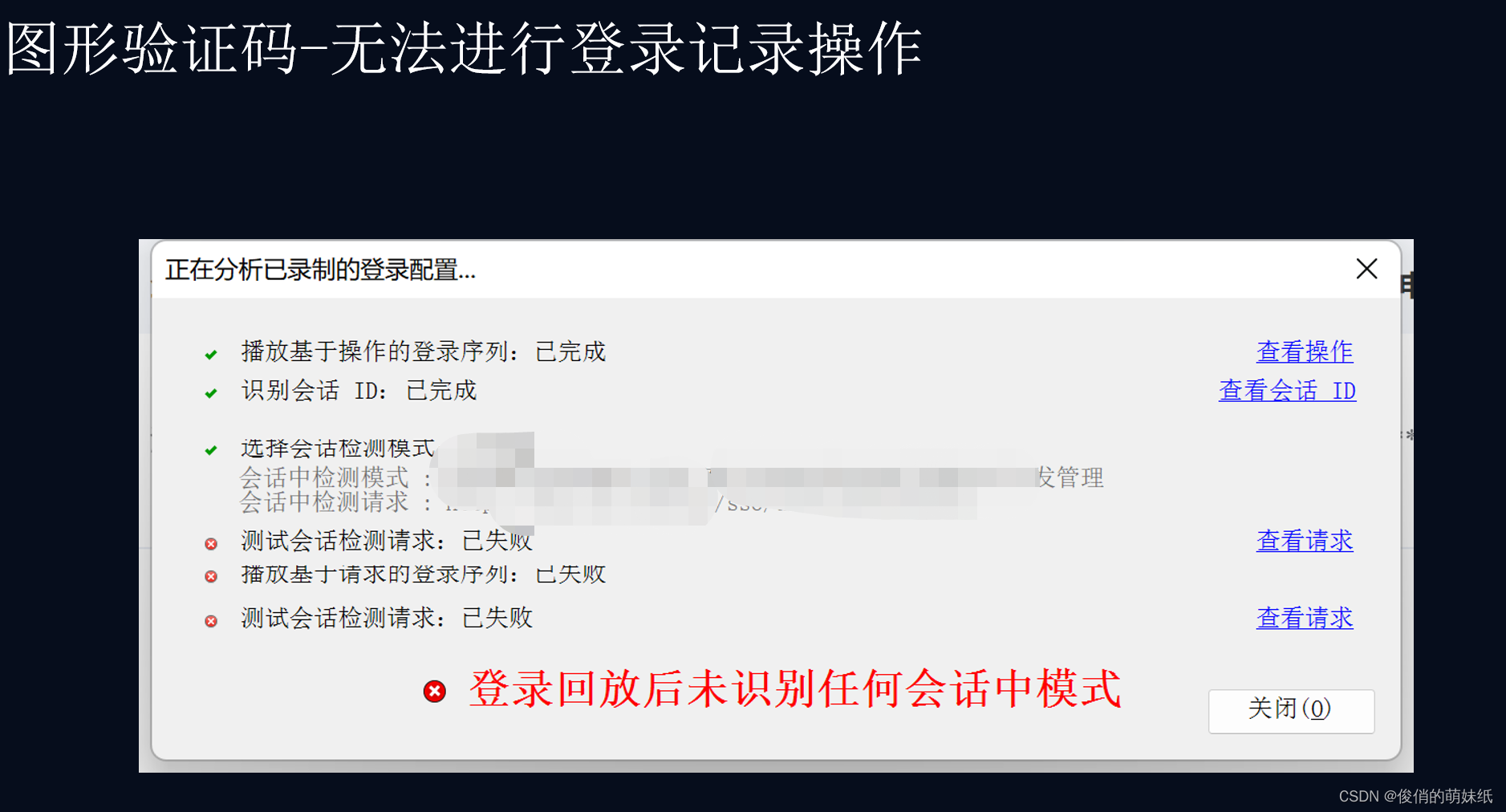
 登录-带图形验证码的系统，如何进行安全扫描？

因为图形验证码会一直更改，appscan无法记录准确的登录信息，所以目前未找到合适的解决方式，可根据上图进行安全扫描也可以的哈

 若扫描过程中，出现中断，卡顿、电脑宕机的情况，appscan自带扫描记忆，下次扫描会从中断的地方进行再次扫描，所以不用担心哈~

扫描完成后，可输出相应安全测试报告，报告中详解解读了产生的原因，以及给出了解决的方案和方式，报告可以说是很详尽了，中英文都有~~

 对于日常系统中，appscan还是可以很好的解决一部分潜在的安全性问题，可以帮助前端后端同学，更好的设计代码和代码架构~~

appscan还有很多安全测试策略，可供各种安全扫描，总体来说，还是很强大的~，感兴趣的小伙伴可进行深层次挖掘，有问题可留言~~，互相学习，共同促进！