【本文仅供学习记录，概无其他用处，一些图片资源来自网络，侵删】
凸优化是一个简单的优化问题，优化-数学规划概念相同，本课程主要学习的内容包括：凸集、凸函数、凸优化和有关凸优化的一些算法。
优化：从一个可行解的集合中，寻找出最优的元素，如
数据拟合问题，散点，非曲线，最小二乘问题，多用户能量控制问题，图像处理优化问题，恢复不带噪声的图像，TV-L2模型，最短路径问题，约束问题。
优化问题三段定义【回忆】
两个或以上X*，构成最优解集
线性规划，单纯形法
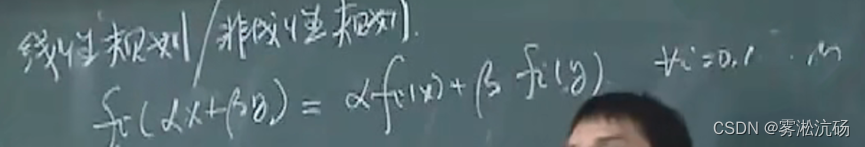
最优解一般在顶点或边上
凸规划/非凸规划【凸规划问题，是容易解决的优化问题，非凸难解决】。
满足以下要求，为凸函数：
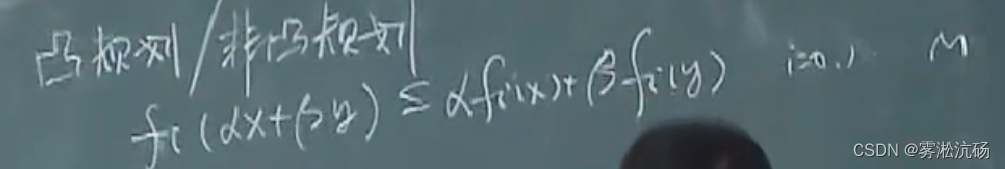
以上线性规划和下方凸规划相关，满足上则满足下
凸优化问题满足：
- 目标函数是凸函数
- 可行解集是凸集
凸函数：没法找到一些不相邻的最低的点
光滑/非光滑，连续/离散【针对可行域，都可能是非凸问题】
单目标/多目标， min f1,f2,pare front[]折衷，加权为单目标
凸规划、单目标。函数光滑容易，讲
目标：简化问题，描述优化，问题凸优化化=90%
主要内容：
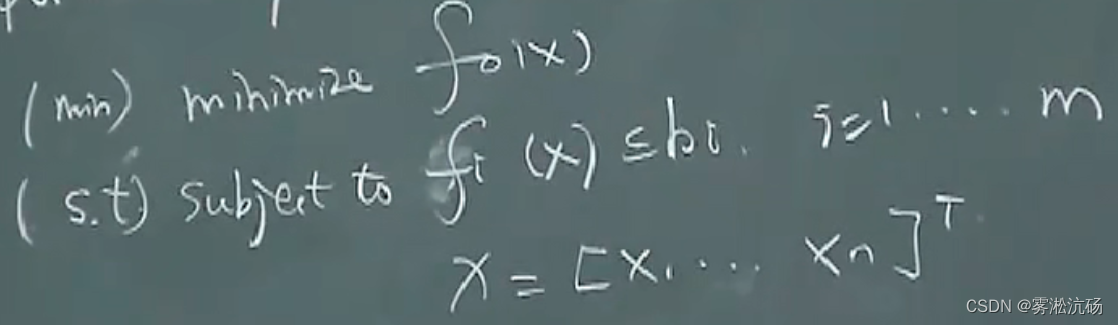
皆可凸优化，平方
描述例1
仿射集【如凸集故事】：/仿射组合/凸组合
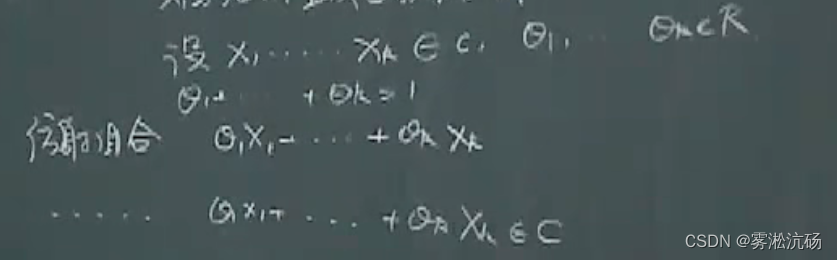
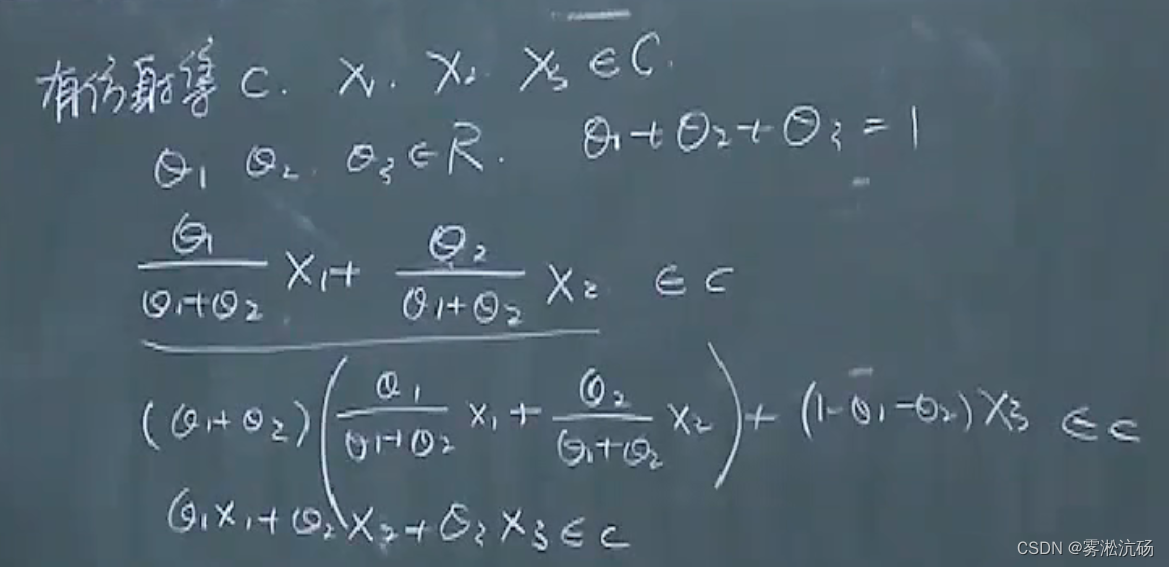证明过程【两点推广到多点（三点）】：
与C相关的子空间V【这个平移x0的仿射集有很好的性质】：
如
，
子空间一定是经过原点的，因为C一定有一点X0，而V减掉了它
证明：
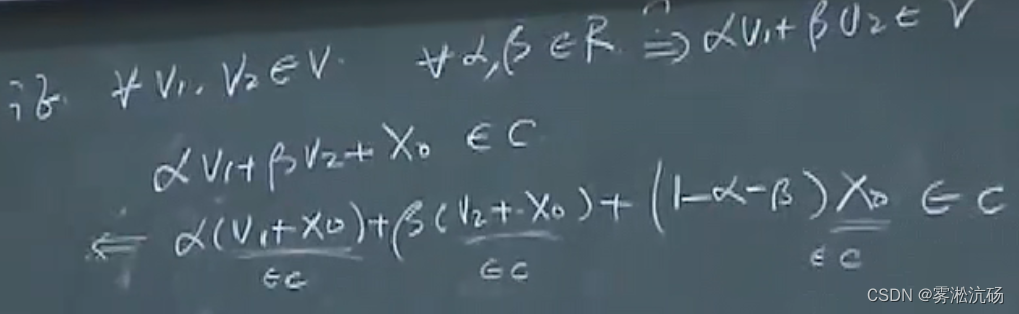
线性方程组的解集一定是个仿射集
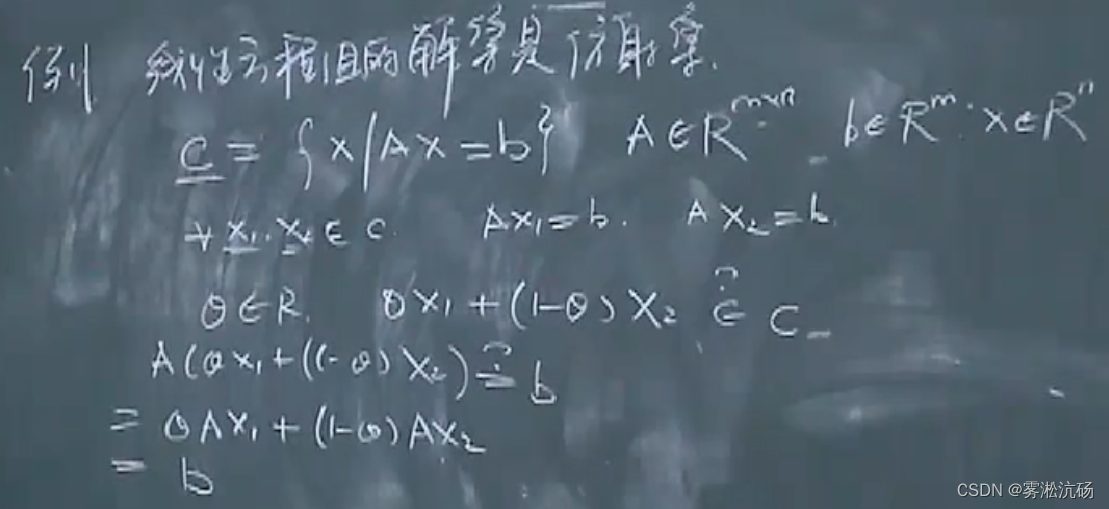
构造尽可能小的仿射集
仿射包：
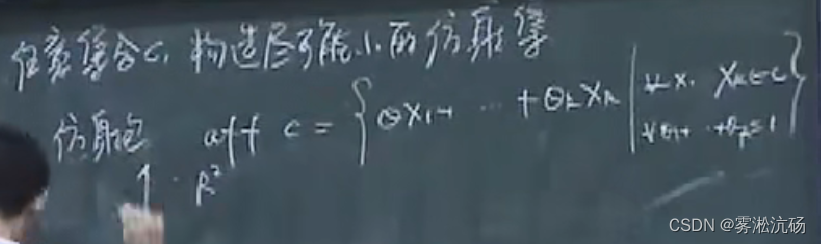
两点直线可定，三点平面可定【全包含】
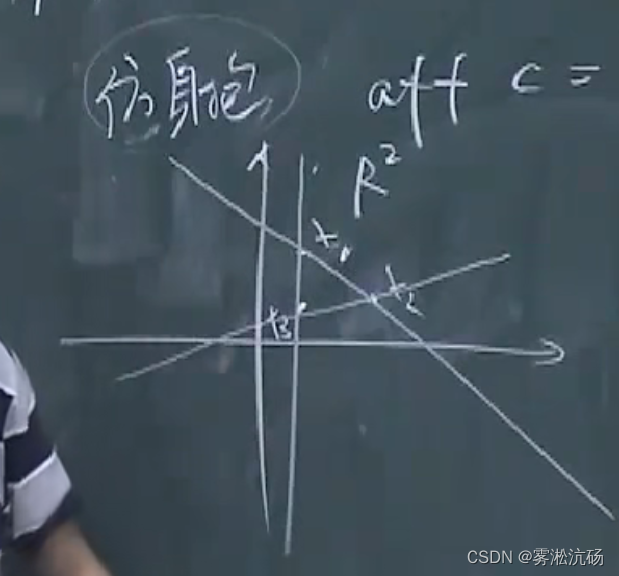
凸集：
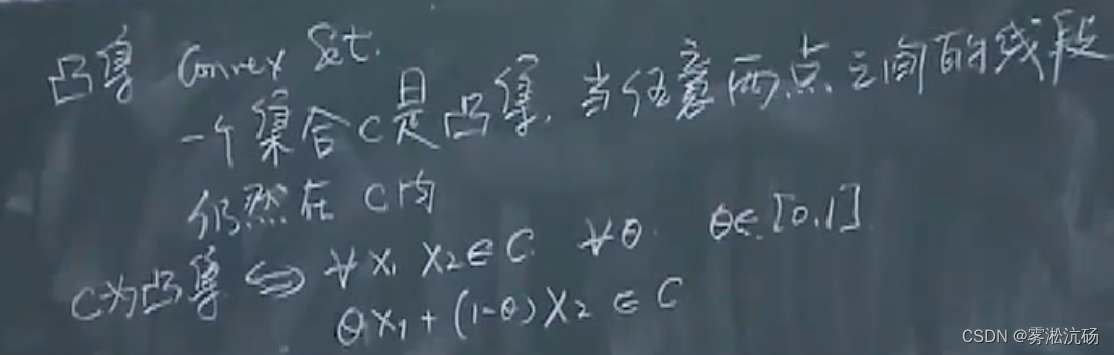
仿射集是一个凸集的特例
X1,………Xk的凸组合：
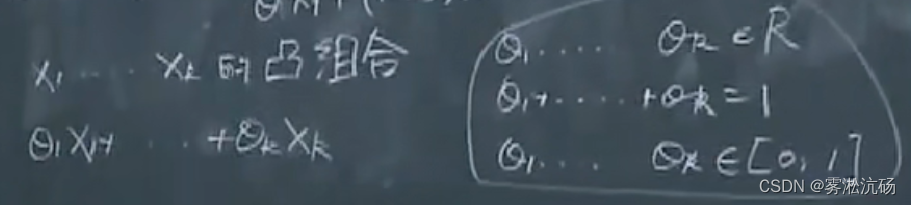
凸包：一个集合构造【扩大】出来最简单的凸集
离散集合的凸包：边缘绑起来【包：包含】
锥，凸锥：【凸锥一定经过原点】
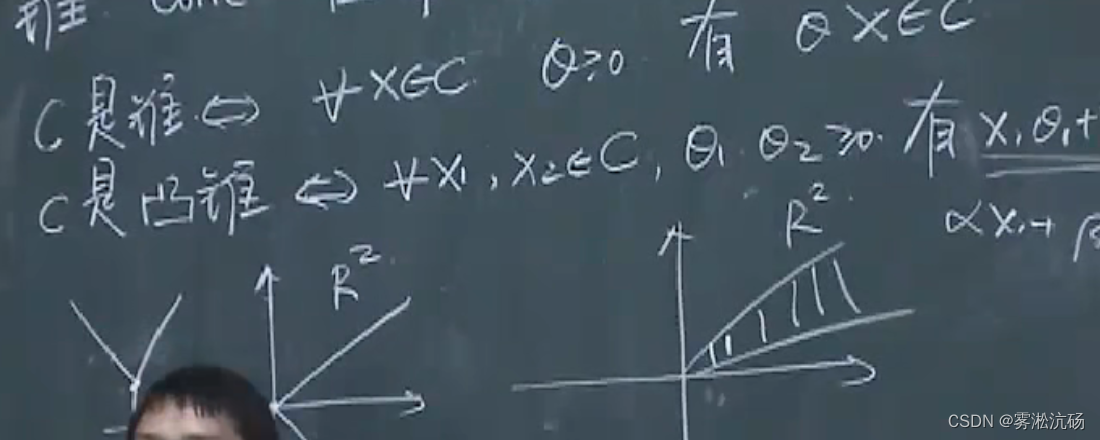
凸锥组合，凸锥包：
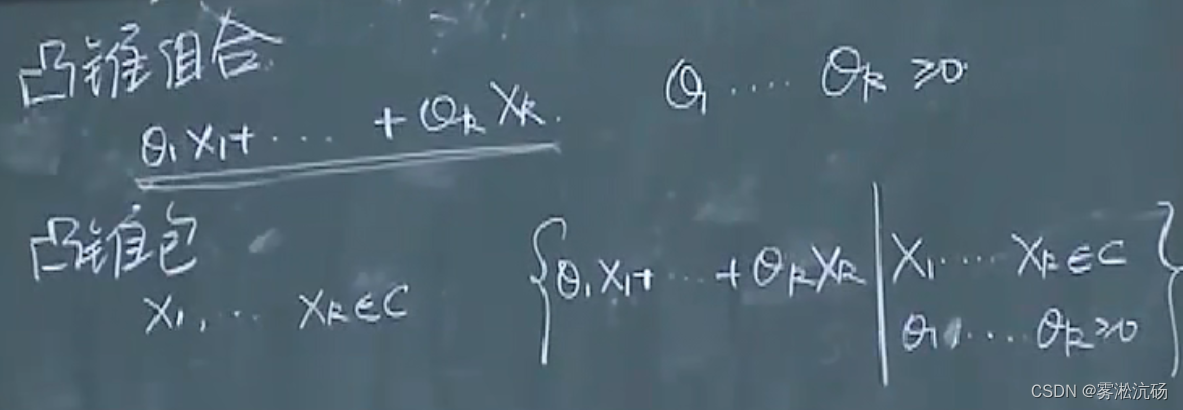
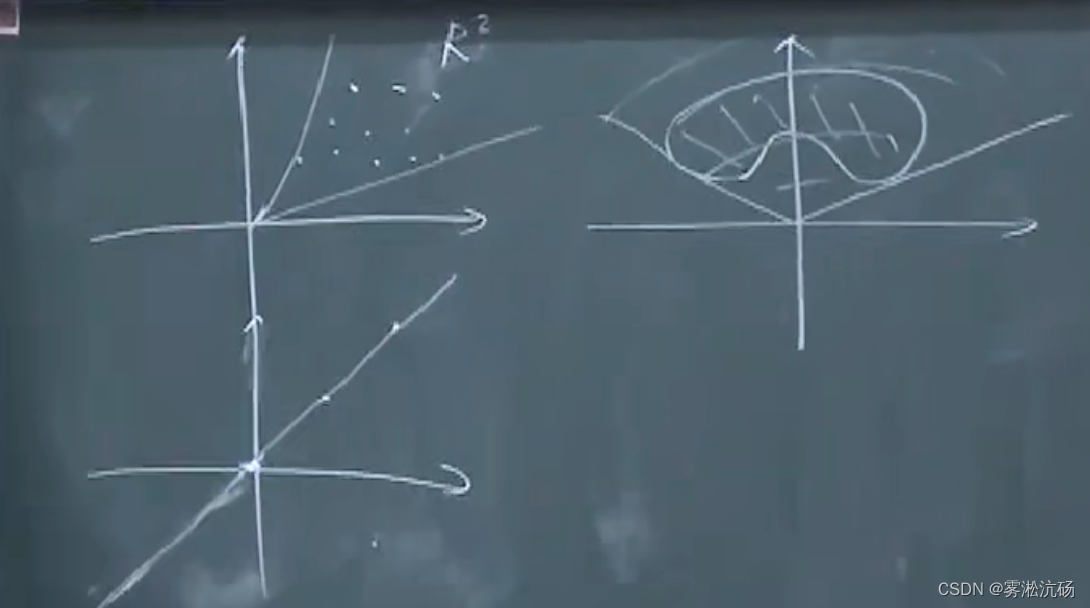
关系：
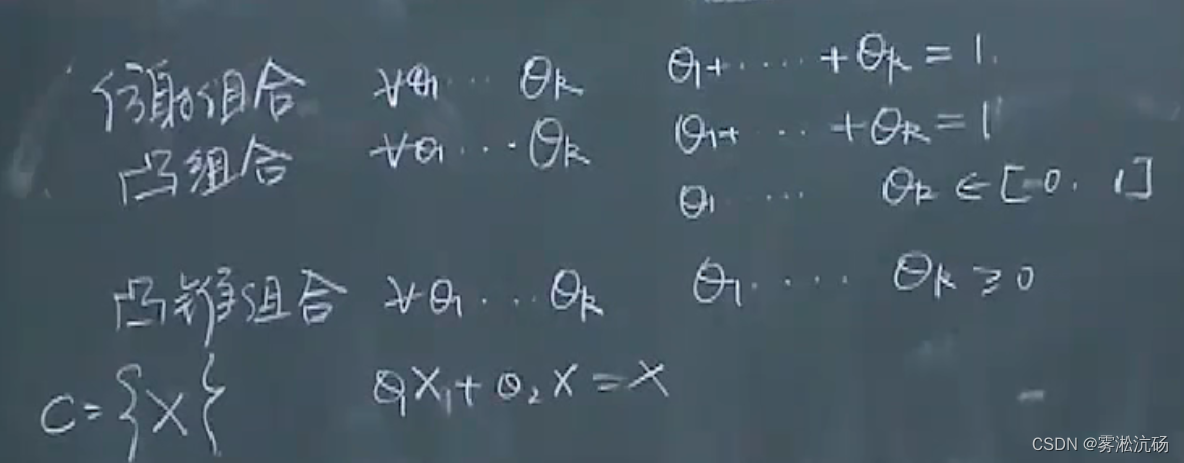
任意的一个点一定是仿射集，也是凸集
空集既是仿射集，又是凸集，又是凸锥
九个概念，组合思想：
超平面，半空间
多面体
球和椭球
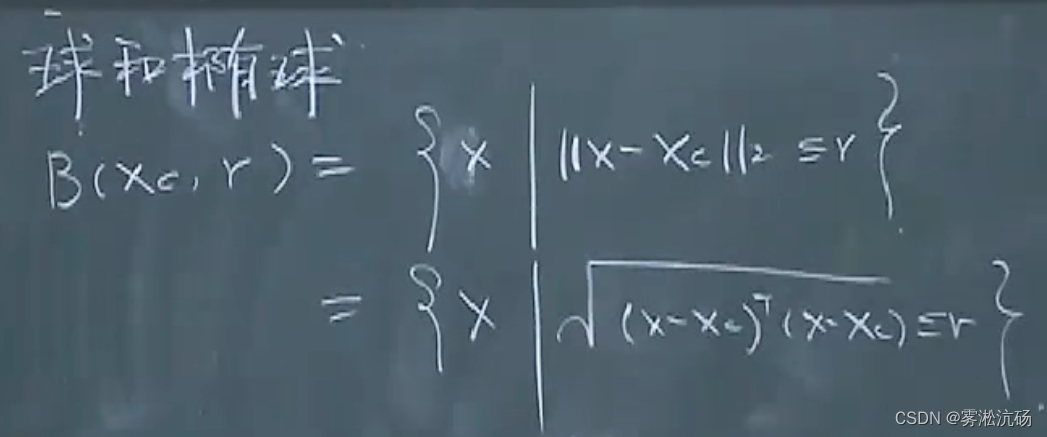
证明球内凸集
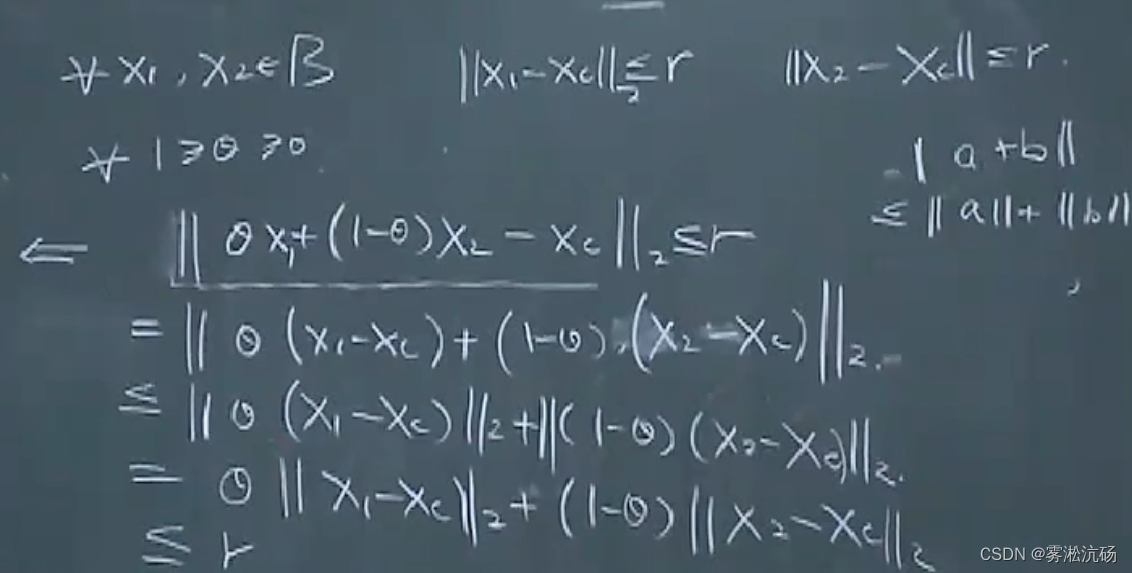
椭球：XT A X
奇异值，ATA【对称，防止，特征值大于等于零，对其开方为A的奇异值】
奇异值是椭球两轴长
多面体
单纯形【是特殊多面体】的证明：
对称矩阵，对称半正定矩阵，对称正定矩阵三个集合都是凸锥：
可用定义证明
凸集：球，椭球，多面体【有很多面的，放的东西】，单纯形
单纯形定义：点，线性无关，凸包
矩阵空间
凸集变换：
- 凸集交集为凸集，两个凸集的和是凸的【S1+S2】，凸加非凸可能凸
- 凸集仿射变换【映射、逆映射】仍是凸集【例如皮球拉伸】
- 缩放与移位都是保凸的
线性矩阵不等式，的解集也是个凸集
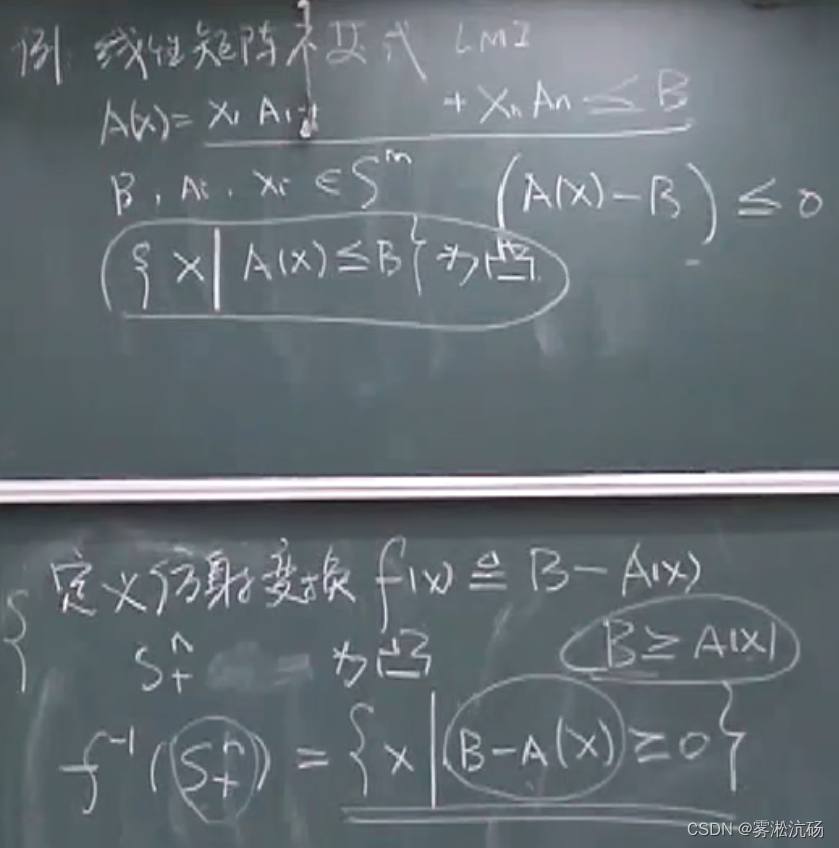
椭圆是球的仿射映射
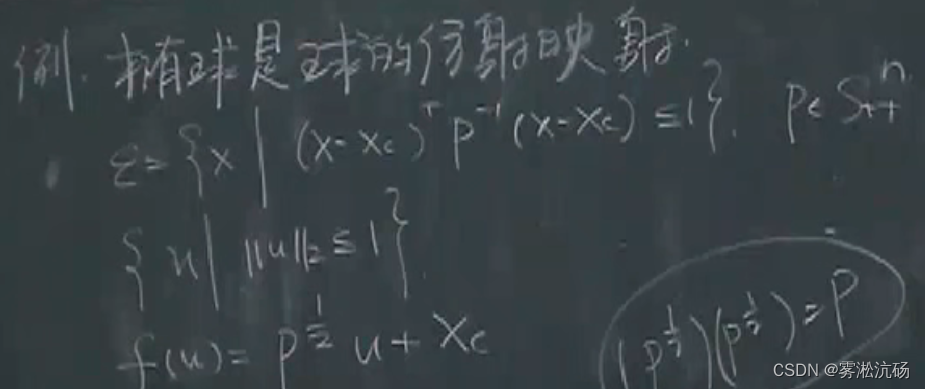
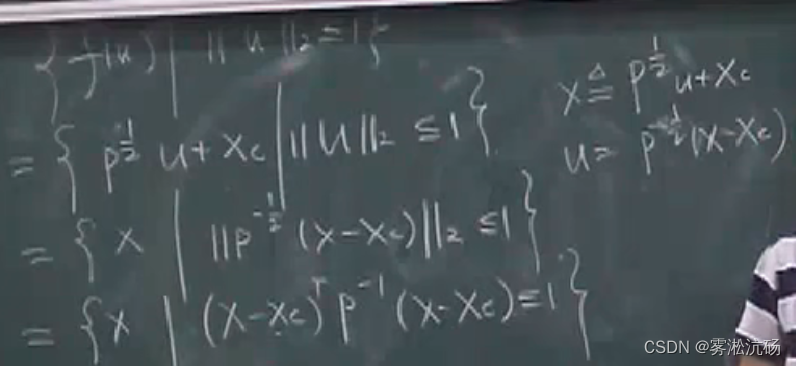
透视函数【降维】，最后一个为正
线性分数函数
