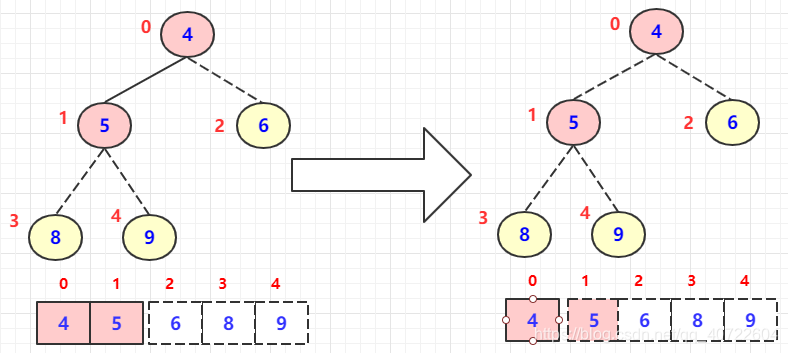
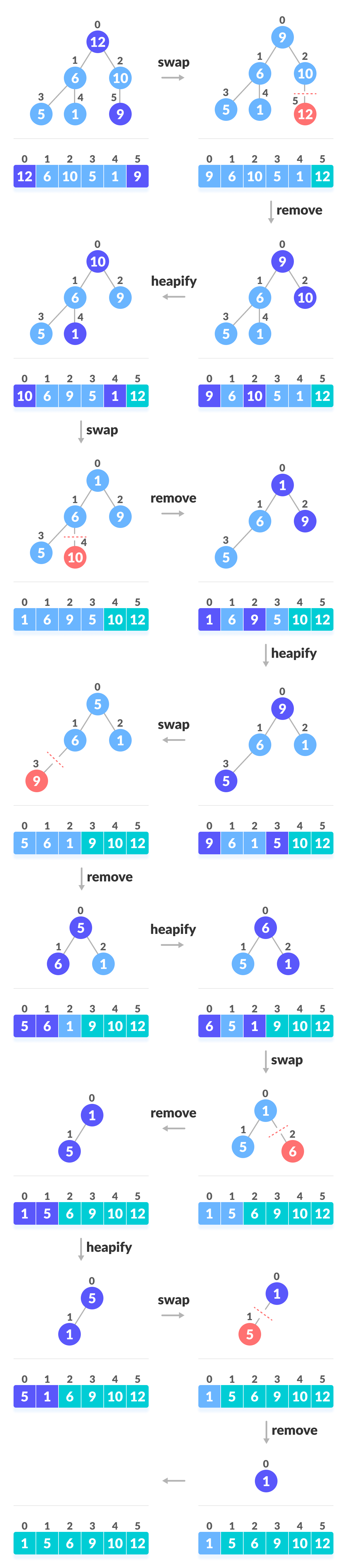
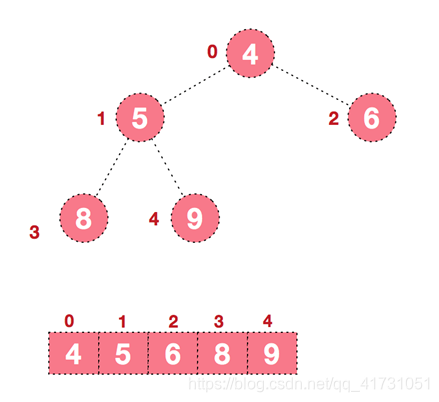
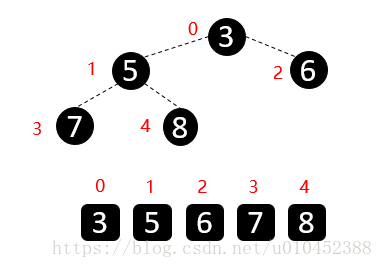
堆排序:结构逻辑上是完全二叉树,但是可以使用顺序存储来实现

一些二叉树的区别:

二叉树:度数最大为2并且每个子树也是二叉树

满二叉树:每层节点都是满的,没有空缺,也就是,叶子节点只能出现在最后一层

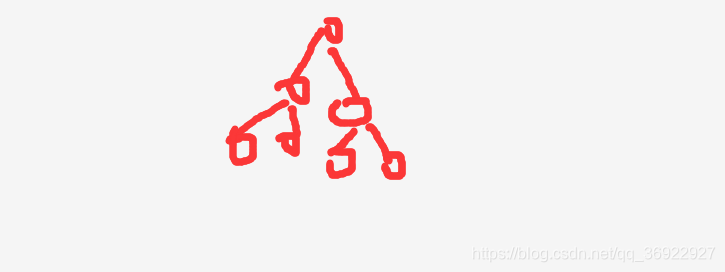
完全二叉树:限制条件比满二叉树弱化,只需要前k-1层是满二叉树结构,最后一层的叶子节点都靠左排列,右侧可以出出现连续缺失(一个学序列可以按照编号一一对应上满二叉树的节点编号)

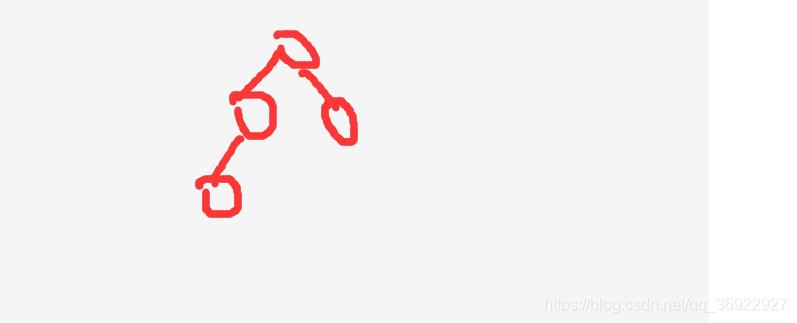
以下不是满二叉树结构：

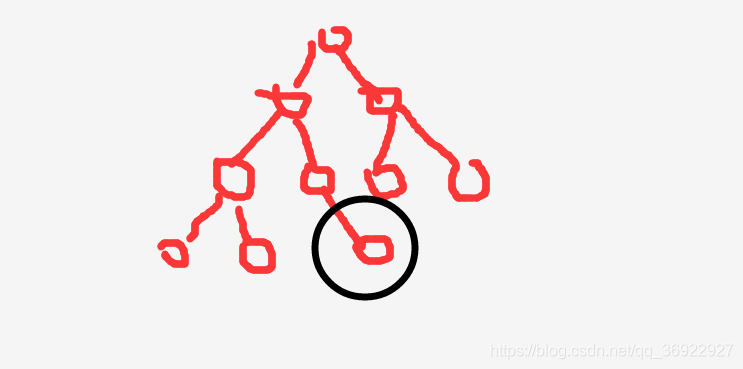
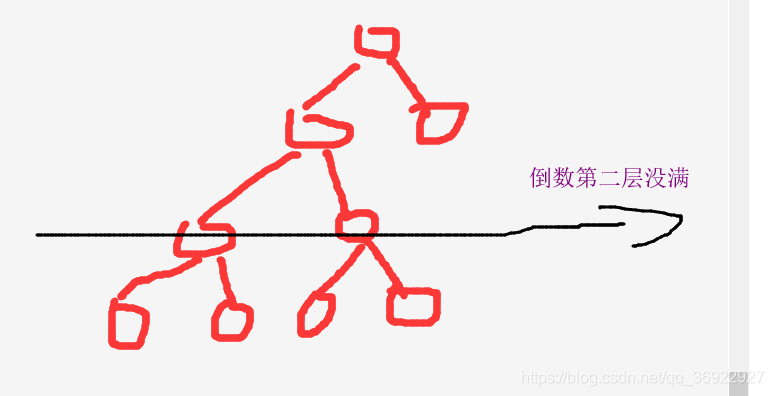
排序二叉树: 二叉树的基础上,加上 中序遍历是有序输出这一要求
平衡二叉树:排序二叉树的基础上,加上要求左右子树的深度差的绝对值只能是0或者1

现在回到堆排序:
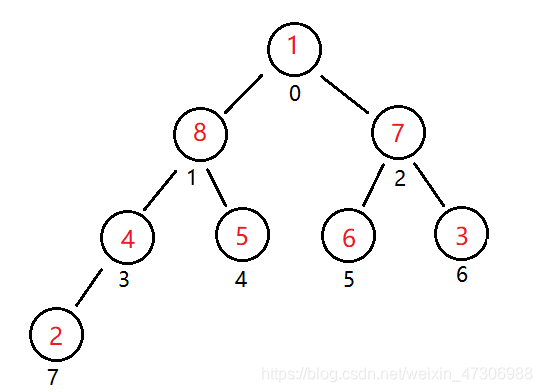
具体满足什么条件的才是堆呢?
以大根堆为例: 对于每棵子树,都满足 根与左右孩子节点相比中最大的元素

堆排序的算法流程:

1. 堆的初始化(将输入序列调整为符合堆的性质)
2. 输出堆顶元素(将堆顶元素与堆尾元素交换,堆的大小-1)
3. 调整堆结构
4. 重复2 3 ,直到全部输出(堆大小变为0)

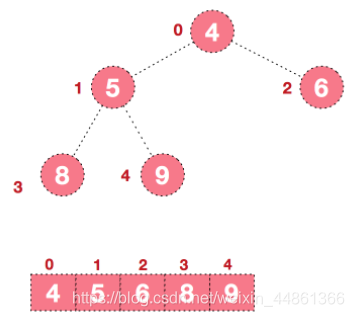
假设堆的编号是从0 开始
那么编号i的节点 (这规律没啥记忆的,画几个圈看下规律即可)
父节点：（ｉ－１）／２
左孩子: 2*i+1
右孩子:2*i+2
最后一个非叶子节点编号：　假设堆共有ｎ个节点，那么最后一个非叶子节点编号为　ｎ／２－１

java代码实现:

/*** @author  wangwei* @date     2019/3/9 8:52* @classDescription   完全二叉树:比满二叉树条件稍弱*                      一共k层的完全二叉树,只要求第k-1层是满的*                      并且第k层的节点集中在左侧,也就是右侧可能出现连续缺失情况**                      大顶堆:根最大,每课子树只保证根大于左孩子,大于右孩子,但是不保证左右孩子之间的大小关系**          给定序列,如何判断是否为堆呢?*          将序列按照层次遍历的形式,构建完全二叉树,观察即可*          比如:1  4 3  7 8 5*              1*             / \*            4   3*          /  \  / \*          7   8 5*    显然是小根堆**    堆排序思想:*    1.以初始关键字序列,构建堆*    2.输出堆顶最小元素*    3,调整剩余元素,使其成为新堆*    4,重复2,3 直到n个元素全部输出,得到一个有序序列**    如果输入为数组:*    当前为i  (i从1开始)*    则左孩子为 2*i*     右孩子:   2*i+1***     堆调整:将堆顶输出,最后孩子放置在堆顶,对剩余元素进行调整*            新堆顶与左右孩子比较,*           与较小孩子交换*           直到调整到叶子节点或者是 比左右孩子都小时,停止调整*      如何初始化序列建堆:从最后一个非叶子节点开始,向上调整,直到根节点*      //      最后一个非叶子节点是  n/2  向下取整****      问题:为什么堆适合线性存储*      答:因为堆是完全二叉树结构,堆中元素的位置能根据父节点索引计算得到，*      所以不需要左右指针也可以找到子节点的位置**/
public class HeapSort {public  void init(int []array){if(null==array||0==array.length){return;}// 注意:计算  左孩子 2*i  ,这里表示编号是从1 开始//               数组从0开始,则需要是 2*i+1//               右孩子:2*i+2//  最后一个非叶子节点 索引:  n/2-1// 最后一个非叶子节点,可能只有左孩子for(int index=array.length/2-1;index>=0;index--){int parent=array[index];int lChild=array[2*index+1];// 只有左孩子if(2*index+2>array.length-1){if(parent>lChild){array[index]=lChild;array[2*index+1]=parent;}}// 左右孩子都有else {int rChild=array[2*index+2];// 处理  parent 不是三者之中最小的int minChildIndex=lChild<rChild? 2*index+1:2*index+2;if(parent>array[minChildIndex]){array[index]=array[minChildIndex];array[minChildIndex]=parent;}}}}//      waitAdjust  堆顶元素,此函数就是为了将其调整到特定位置,满足小顶堆//    索引在 minHeapEnd  是表示当前堆的最后一个元素索引//public void adjustHeap(int []array,int minHeapEnd){int currentIndex=0;int waitAdjust=array[0];while (currentIndex<=minHeapEnd/2-1){int leftChild=array[2*currentIndex+1];// 只有左孩子if(2*currentIndex+2>minHeapEnd){if(leftChild>waitAdjust){array[currentIndex]=leftChild;currentIndex=2*currentIndex+1;// 走向左子树}}// 左右孩子都有: 选取最小孩子交换else{int rChild=array[2*currentIndex+2];int minChildIndex=leftChild<rChild? 2*currentIndex+1:2*currentIndex+2;if(waitAdjust<=array[minChildIndex]){break; // 结束调整}else {array[currentIndex]=array[minChildIndex];currentIndex=minChildIndex;}}}array[currentIndex]=waitAdjust;}//将堆顶元素交换到tail  (这里看作是输出)public void pop(int[] array,int tail){int temp=array[0];array[0]=array[tail];array[tail]=temp;}public void heapSort(int array[]){if(null==array||0==array.length){return;}init(array);for(int i=0;i<array.length;i++){pop(array,array.length-1-i);// 注意堆调整的范围比之前的少一个元素adjustHeap(array,array.length-1-i-1);}}public static void main(String[] args) {int [] array= {2,5,3,12,8,17,10,20,19,13};RandomUtil.printArray(array);new HeapSort().heapSort(array);System.out.println("排序后:");RandomUtil.printArray(array);}
}

输出:

几个方法说明:

init(): 将输入序列初始化为堆
pop(int[] array,int tail): 输出,将堆顶元素交换到当前堆的 ** 最后一个位置 **
adjustHeap(int []array,int minHeapEnd): 调整堆,堆顶元素是来自堆尾的,可能不满足堆的性质,需要将其调整到
合适的位置
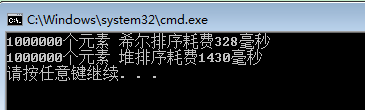
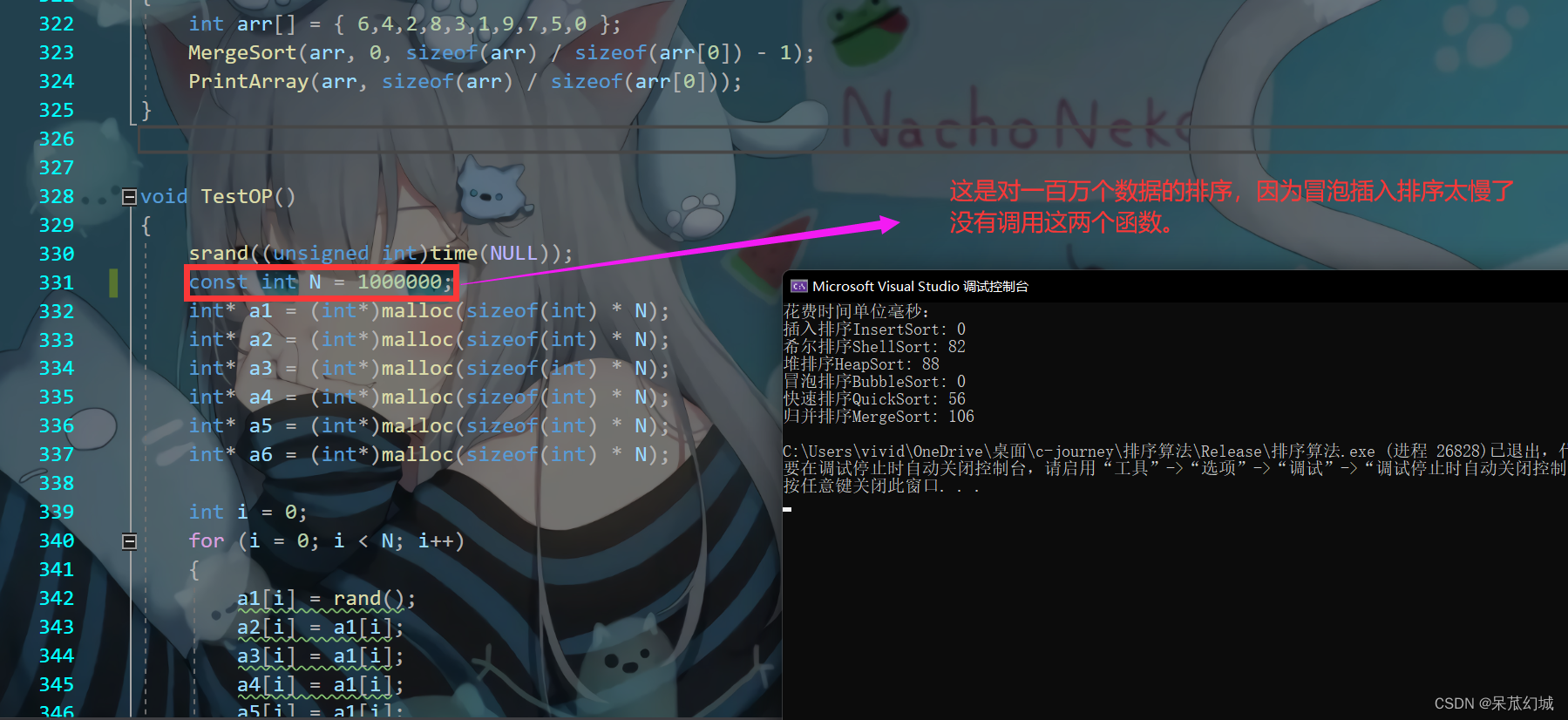
时间复杂度:初始化是ｏ（ｎ）　，调整重建是ｏ（ｌｇｎ），共需要ｎ次重建　记为ｏ（ｎｌｇｎ）
流程是：
初始化；／／　ｏ（ｎ）
ｗｈｉｌｅ（ｉ＋＋＜ａｒｒａｙ．ｌｅｎｇｔｈ）｛／／ｏ（ｎ）
ｐｏｐ（）；
ａｄｊｕｓｔ（）；／／（ｏ　ｌｇｎ）
｝

总的时间复杂度＝ｏ（ｎ）＋ｏ（ｎｌｇｎ）＝ｏ（ｎｌｇｎ）
空间复杂度：只是使用了有限个简单变量，ｏ（１）

注意：堆初始化和堆调整有些相似，但是是不一样的．
　　　　堆初始化：自底向上调整
　　　　堆调整：自上向下重建堆

堆排序的优化（只是一个思路，未证明）：

（小顶堆为例）
堆排序哪里可以优化呢，都这么优秀了？
堆调整可能被优化，将堆尾元素与堆顶交换，而堆尾元素可能是是很大的，那么调整时，就会与很多层去比较，如何减少这个层的比较呢？

堆中从根节点到叶节点的一条路径是有序的

　　　　３／　　＼　４　　　５／　＼　　／＼７　　６　　８　１０
现在需要将堆顶给移出，交换成如下树　　ｈ＝３１０／　　＼　４　　　５／　＼　　／＼７　　６　　８　３
／／　ｈ／２＝１　　
／／　根　１０　　与４　比较　１０＞４
／／　交换　根成为４４／　　＼　１０　　５／　＼　　／＼７　　６　　８　３／／　　　１．　调整子树　　　１０／　　＼７　　　６／／　２．　根４与５比较，，根较小，不调整

可能的运用场景

ｔｏｐ（ｋ）：时间复杂度　　ｎ（ｌｇｋ）