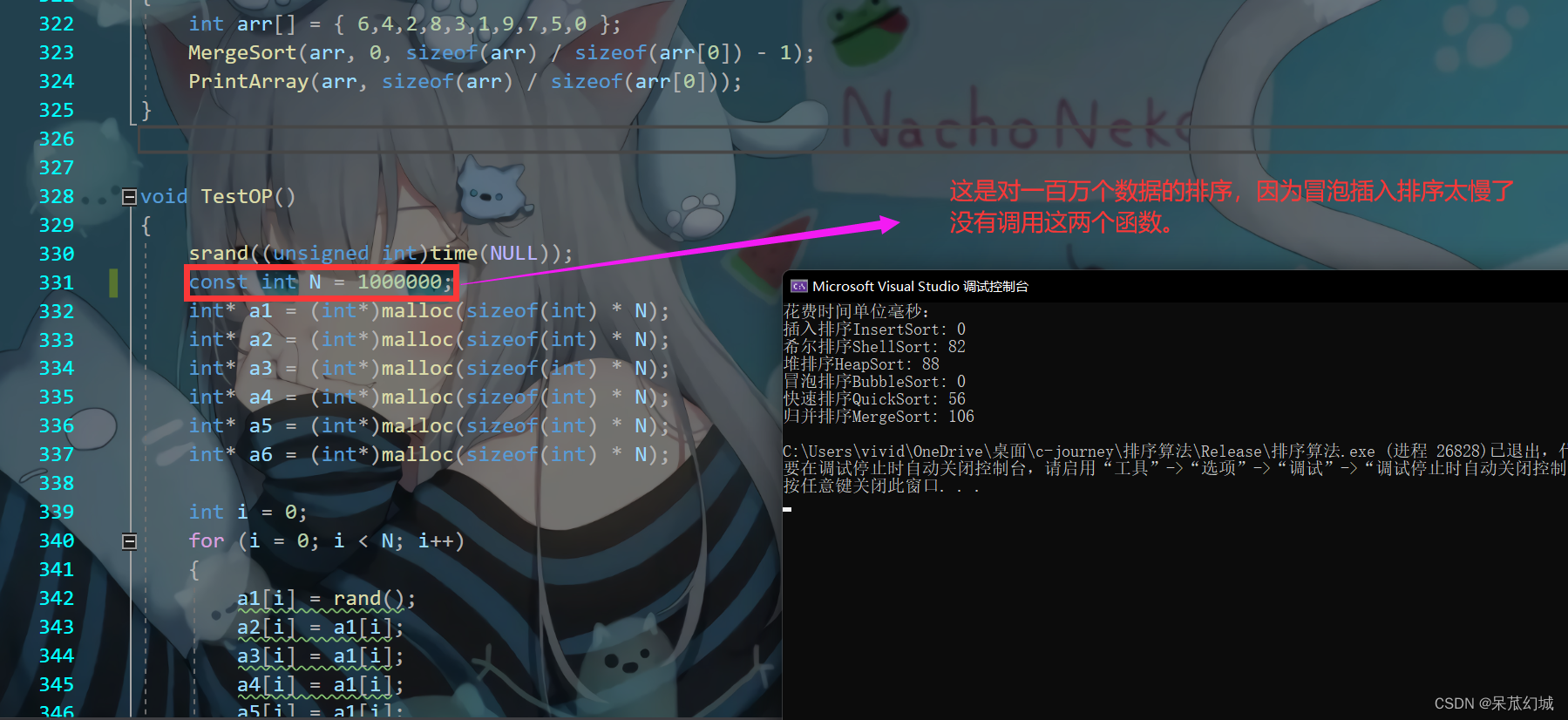
文章目录
- 准备知识
- MAX-HEAPIFY过程
- 建堆
- 堆排序算法
- 总结
准备知识
堆的结构可以分为最大堆和最小堆,是一个完全二叉树,而堆排序是根据堆的这种数据结构设计的一种排序。
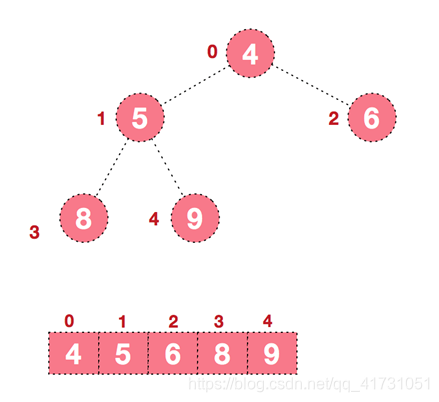
所谓完全二叉树即叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
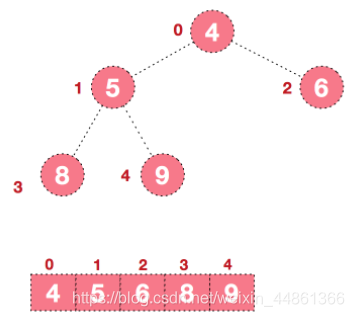
存储一个完全二叉树,最适合使用数组,因为它相比链表不需要存储左、右子树的指针,更加节省内存空间,通过数组索引即可以随机访问到对应元素。

假设你知道某个节点下标为x ,那么其左子树下标为 x *2+1,其右子树下标为 x *2+2 ,其父节点下标为 (x-1)/2。
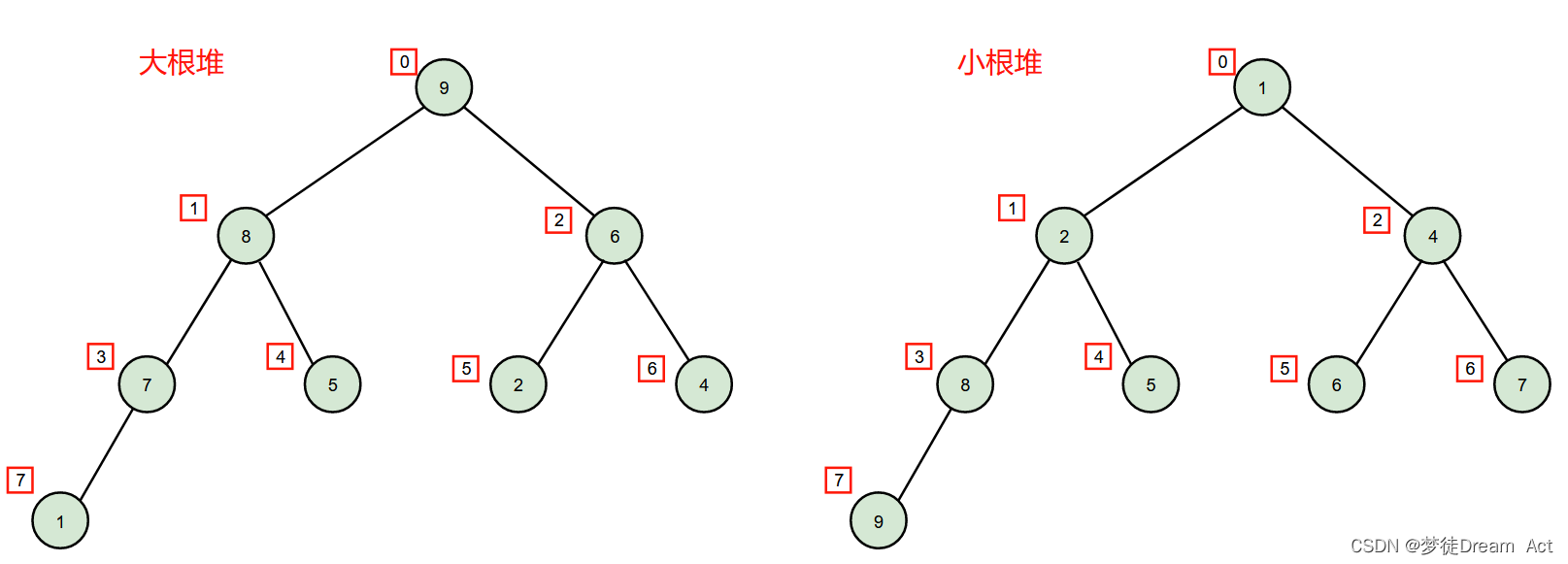
每个结点的值都大于其左孩子和右孩子结点的值,称之为最大堆(大根堆);
每个结点的值都小于其左孩子和右孩子结点的值,称之为最小堆(小根堆)。
如果把堆看成一棵树,我们定义一个堆中的节点的高度就为根节点到叶节点最长简单路径上边的数目。
MAX-HEAPIFY过程
MAX-HEAPIFY过程其时间复杂度为O(lgn),它是维护最大堆性质的关键。
MAX-HEAPIFY是用于维护最大堆性质的重要过程。它的输入为一个数组A和一个下标i。在调用MAX-HEAPIFY的时候,我们假定根节点为LEFT(i)和RIGHT(i)的二叉堆都是大根堆,但这时A[i]有可能小于其孩子,这样就违背了大根堆的性质。
MAX-HEAPIFY通过让A[i]的值在大根堆中逐级下降,从而是的以下标为i为根节点的字数重新遵循大根堆的性质。
//arr为堆,len为堆的长度,idx为非叶节点下标
void adjust(vector<int>& arr, int len, int idx) {int left = 2 * idx + 1;//idx的左子节点int right = 2 * idx + 2;//idx的右子节点int maxidx = idx;//maxidx为左右子节点及当前节点中最大的那个//判断最大节点是不是左右子节点if (left<len && arr[left]>arr[maxidx])maxidx = left;if (right<len && arr[right]>arr[maxidx])maxidx = right;if (maxidx != idx) {swap(arr[maxidx], arr[idx]);//交换根节点和子节点的值adjust(arr, len, maxidx);//交换后的子节点值为插入的节点的值,继续迭代}//else return;//如果最大的就是当前节点的值,则直接结束此次迭代
}
建堆
建堆具有线性时间复杂度O(n),功能是从无序的输入数据数组中构造一个最大堆。
在建堆的时候,我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n的数组转换为大根堆。子数组A(n/2+1…n)中的元素都是树的叶节点。每个叶节点都可以看成只包含一个元素的堆。建堆的过程就是堆树中的其他节点都调用一次MAX-HEAPIFY:
for (int i = n / 2 - 1; i >= 0; i--)//MAX-HEAPIFY(A,i);adjust(arr, size, i);
堆排序算法
heapsort(堆排序)过程其时间复杂度为O(nlgn),功能是对一个数组进行原址排序。
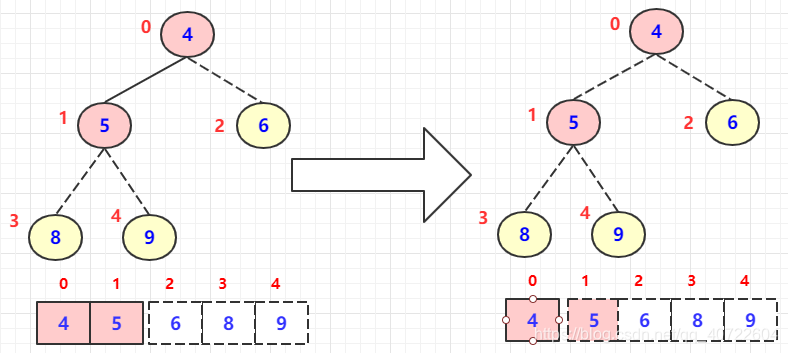
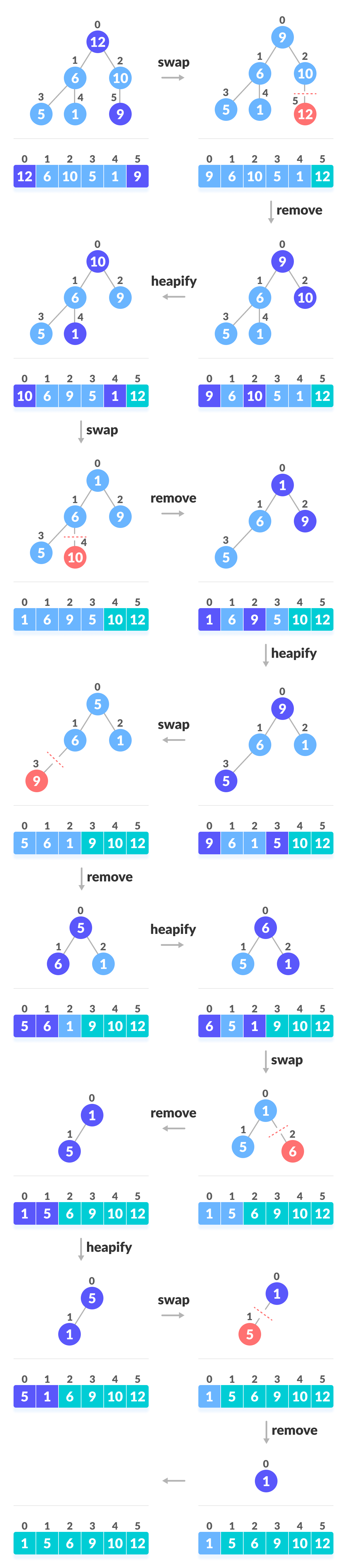
初始的时候,堆排序算法利用建堆过程将输入数组A[1…n] 建成最大堆。
因为数组中的最大元素总在根节点A[1]上,通过把它与A[n]进行交换,我们可以让元素放到正确的位置上。
这时候,如果我们从堆中去掉节点n,剩余的节点中,原来根的左右子节点仍然是最大堆,而新的节点可能会违背最大堆的性质。
为了维护最大堆的性质,我们要做的是利用MAX-HEAPIFY过程重新在A[1…n-1]上构造一个最大堆。堆排序算法会不断重复这一过程,直到堆的大小从n-1降到2。
for (int i = size - 1; i >= 1; i--) {swap(arr[0], arr[i]);//交换根节点与最后一个节点adjust(arr, i, 0);//调整堆为最大堆}
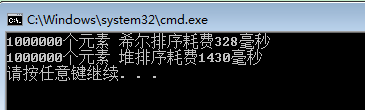
详细图解可见这篇帖子的4.3.3利用大根堆进行排序
总结
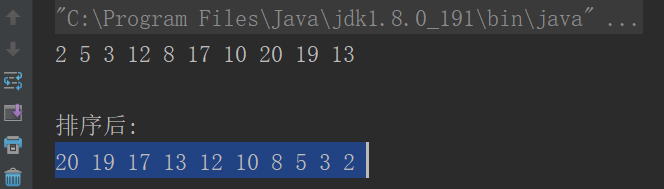
完整的堆排序c++代码如下:
/*堆排序*/
#include<iostream>
#include<vector>
using namespace std;void heapSort(vector<int>& arr, int size);
void adjust(vector<int>& arr, int len, int idx);//递归方式构建大根堆(len是arr的长度,idx是当前节点的下标)
void adjust(vector<int>& arr, int len, int idx) {int left = 2 * idx + 1;//idx的左子节点int right = 2 * idx + 2;//idx的右子节点int maxidx = idx;if (left<len && arr[left]>arr[maxidx])maxidx = left;if (right<len && arr[right]>arr[maxidx])maxidx = right;if (maxidx != idx) {swap(arr[maxidx], arr[idx]);adjust(arr, len, maxidx);}
}void heapSort(vector<int>& arr, int size) {//构建大根堆,从最后一个节点的父节点开始向前遍历for (int i = size / 2 - 1; i >= 0; i--)adjust(arr, size, i);//调整大根堆for (int i = size - 1; i >= 1; i--) {swap(arr[0], arr[i]);adjust(arr, i, 0);}
}int main() {vector<int> arr = { 8, 1, 14, 3, 21, 5, 7, 10 };heapSort(arr, arr.size());return 0;
}