A*算法

A* 搜索算法，即A star search algorithm，简称A* 算法。 是一种在图形平面上对于多个节点的路径求出最低通过成本的算法。是对图的遍历和最佳优先搜索算法，也是对BFS的改进。其思想在于为每个状态建立启发函数，用启发函数制约搜索沿着最有效的方向行进。

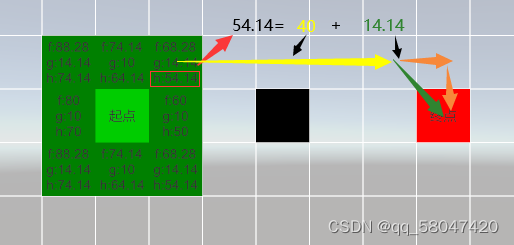
如图为八数码，求将左图变为右图需要的步骤。传统的BFS算法是将0四周的数与0交换，然后将其放入队列中，通过盲目地对有限的数据进行尝试最后求得答案，这样的时间复杂度较为复杂。而A*算法中通过加入启发函数对搜索的优先次序进行约束，以最快的方式得到答案。即$f(n)=g(n)+h(n)$，其中$g(n)$为该状态的实际情况，$h(n)$为启发函数，而得到的$f(n)$即是对状态的估价，用于安排搜索的优先顺序。在该图中，$g(n)$为此刻矩阵的状态，$h(n)$为此刻的矩阵与目标矩阵值不同的坐标的数量。

定理：

定义起点**$s$** ，终点**$t$** ，从起点（初始状态）开始的距离函数$g(x)$ ，到终点（最终状态）的距离函数$h(x),h^{\ast }(x)$ ，以及每个点的估价函数 $f(x)=g(x)+h(x)$。

A*算法每次从优先队列中取出一个 **$f$**最小的元素，然后更新相邻的状态。

如果$h\le h^{\ast }$，则 A* 算法能找到最优解。

上述条件下，如果**$h$**满足三角形不等式，则 A*算法不会将重复结点加入队列。

当时$h=0$，A*算法变为Dijkstra；当并且边权为时变为 BFS。

证明：

复杂度分析：

外循环中每次从open中取出点，共取n次，

内循环：遍历它的邻接点$n(E)$，并将这些邻接点放入open中，对open进行排序，open表大小是$O(n)$量级的，若用快排就是$O(nlogn)$，内循环总的复杂度为$O(n\ast logn+E)=O(n\ast logn)$

总复杂度为$O(n^2\ast logn)$

题目分析：

【八数码难题】

题目描述

在3×3的棋盘上，摆有八个棋子，每个棋子上标有1至8的某一数字。棋盘中留有一个空格，空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为123804765），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

输入格式

输入初始状态，一行九个数字，空格用0表示

输出格式

只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数(测试数据中无特殊无法到达目标状态数据)

输入输出样例

输入 #1复制

283104765

输出 #1复制

4

题目来源：https://www.luogu.com.cn/problem/P1379

试题解析：

首先，我们创建两个字符串，str_s用于读入起始状态，str_e用于存储目标状态，在样例中即为str_s=“283104765”,str_e=“123804765”。然后将起始状态读入。

创建a_star函数，利用STL中的unordered_map函数创建哈希表：unordered_map<string,int>dist（用于存储由起始状态到状态的变化次数）和unordered_map<string,bool>vis（用于表示该状态是否被访问过）。然后是优先队列priority_queue<pair<int,string>,vector<pair<int,string>,greater<pair<int,string>>>q，该优先队列用于存储每个点的估价函数，即$f(n)=g(n)+h(n)$，然后根据估价函数进行小根堆排序，估价距离目标状态最近的状态优先弹出。

不断访问并弹出队头元素，如果该状态已经被访问过，则取下一个元素，直到队头状态未被访问为止。将该状态标记为true，表示其已经被访问过。将字符串遍历一遍，找到0的位置，将其在二维数组中的坐标表示出来（当前下标/3为x，当前下标%3为y）。然后根据其二维坐标进行交换，分别上下左右四个坐标交换，如果交换之后的状态未曾出现或者可以更新为更短的距离，则更新，然后加入到队列中。

最后返回目标状态的dist即可。

#include<bits/stdc++.h>
using namespace std;string str_s, str_e = "123804765";//起始状态和目标状态int f(string start)//求该状态的估价函数
{int res = 0;for (int i = 0; i < 9; i++)if (start[i] != str_e[i])res++;return res;z
}int a_star(string start)
{int mx[4]{ 0,-1,0,1 }, my[4]{ -1,0,1,0 };//偏移数组，用于交换坐标点unordered_map<string, int>dist;//存储距离unordered_map<string, bool>vis;//标记该状态是否访问过priority_queue < pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>>q;//优先队列q.push({ f(start),start });//存入该状态的估价函数和状态while (!q.empty()){auto t = q.top();//取队头元素q.pop();if (t.second == str_e)break;//如果当前弹出的状态于目标状态一致时，则退出循环if (vis[t.second])continue;//如果该状态被访问过时，逃过本次循环string p = t.second;vis[p] = 1;int step = dist[p];int x, y;for (int i = 0; i < 9; i++)//遍历得到0的坐标if (p[i] == '0'){x = i / 3, y = i % 3;break;}for (int i = 0; i < 4; i++){int a = x + mx[i], b = y + my[i];if (a < 0 || a >= 3 || b < 0 || b >= 3)continue;//如果交换之后的坐标越界，则跳过本次操作swap(p[x * 3 + y], p[a * 3 + b]);//将两坐标交换if (!dist.count(p) || dist[p] > step + 1)//状态为存储或能更新为更小值{dist[p] = step + 1;//更新状态q.push({ dist[p] + f(p),p });//将状态加入优先队列中}swap(p[x * 3 + y], p[a * 3 + b]);//将状态复原}}return dist[str_e];//返回移动步骤次数
}int main()
{cin >> str_s;cout << a_star(str_s) << endl;return 0;
}