A星算法（Java实现）

article/2025/10/2 20:19:29

一、适用场景

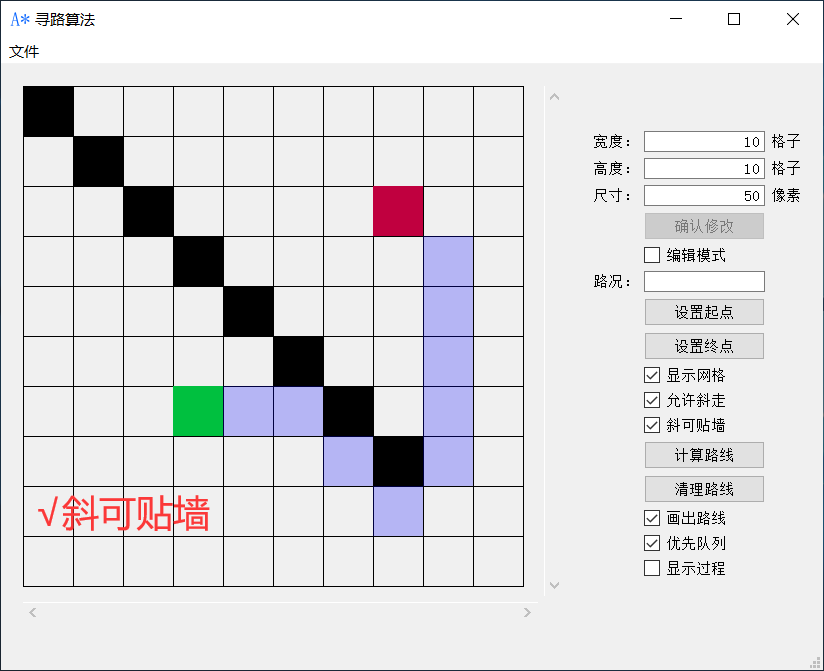
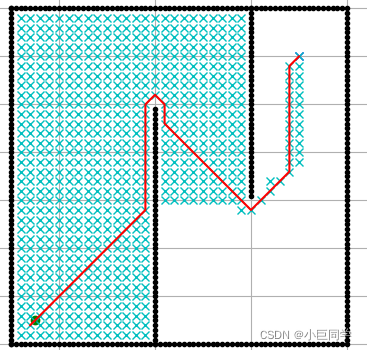
在一张地图中，绘制从起点移动到终点的最优路径，地图中会有障碍物，必须绕开障碍物。

二、算法思路

1. 回溯法得到路径

(如果有路径)采用“结点与结点的父节点”的关系从最终结点回溯到起点，得到路径。

2. 路径代价的估算：F = G+H

A星算法的代价计算使用了被称作是启发式的代价函数。
先说明一下各符号意义：G表示的是从起点到当前结点的实际路径代价(为啥叫实际？就是已经走过了，边走边将代价计算好了)；H表示当前结点到达最终结点的估计代价(为啥叫估计？就是还没走过，不知道前面有没障碍、路通不通，所以只能用估计)；F表示当前结点所在路径从起点到最终点预估的总路径代价。

G的计算方式：计算方式有挺多种的，这里我们就用这种吧，假设每个结点代表一个正方形，横竖移动距离：斜移动距离=1：1.4（根号2），我们取个整数10和14吧，也就是说当前结点G值=父节点的G+（10或14）。

H的计算方式：估价计算也有很多种方式，我们这里使用“曼哈顿”法，H=|当前结点x值-最终结点x值|+|当前结点y值-最终结点y值|（"||"表示绝对值）。

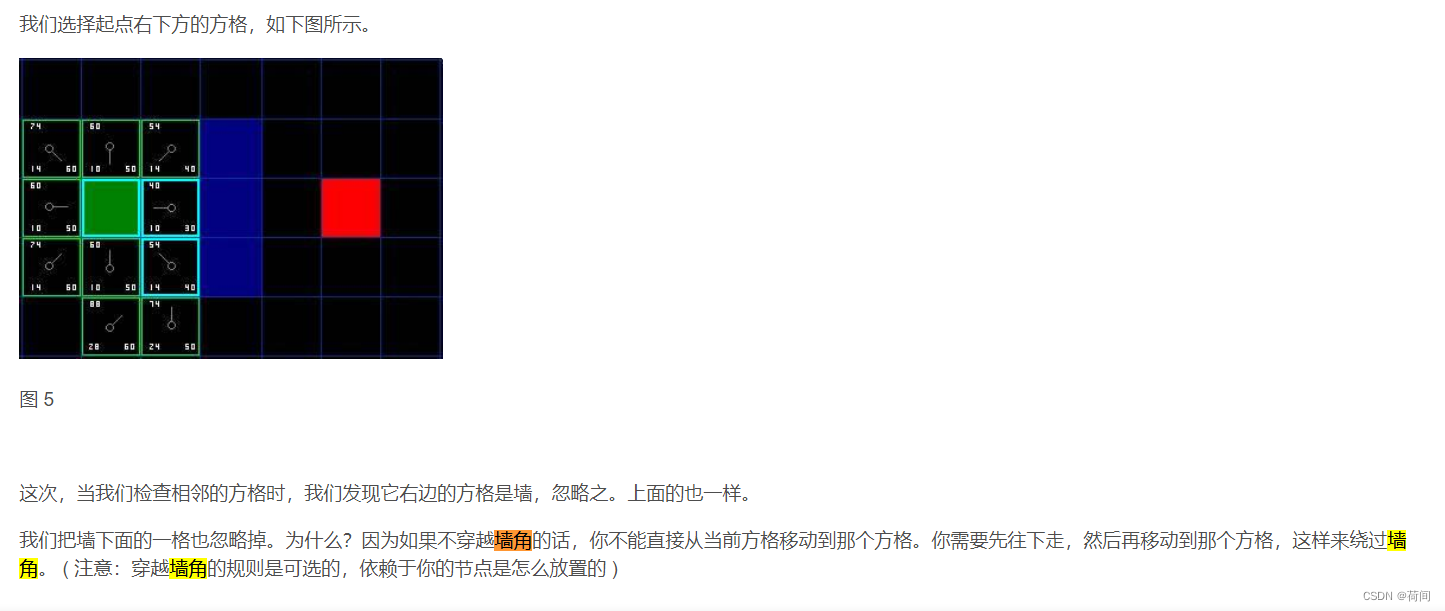
如下图（图不是自己做的，从网上借来的，自己画的话~…惨不忍睹！）

3. 辅助表：Open、Close列表

在A星算法中，需要使用两个辅助表来记录结点。
一个用于记录可被访问的结点，成为Open表；一个是记录已访问过的结点，称为Close表。
这两个表决定了算法的结束：条件是最终结点在Close表中(找到路径)或Open表为空(找不到了路径)。

4. 移动结点、相邻结点的处理

上面的理解的话，现在就来移动当前的节点，寻找路径。

每次从Open表中取出F值最小的结点出来（这里我们使用优先队列来处理比较好），作为当前结点；然后将当前结点的所有邻结点按照邻结点规则加入到Open表中；最后将当前结点放入Close表中，这里就是每次循环的执行内容。

邻结点规则：
(1) 当邻结点不在地图中，不加入Open表；
(2) 当邻结点是障碍物，不加入Open表；
(3) 当邻结点在Close表中，不加入Open表；
(4) 当邻结点不在Open中，加入Open表，设该邻结点的父节点为当前结点；
(5) **当邻结点在Open表中，我们需要做个比较:如果邻结点的G值>当前结点的G值+当前结点到这个邻结点的代价，那么修改该邻结点的父节点为当前的结点(因为在Open表中的结点除了起点，都会有父节点)，修改G值=当前结点的G值+当前结点到这个邻结点的代价 **

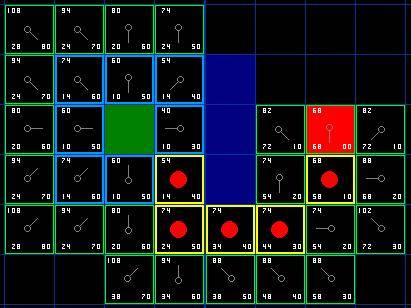
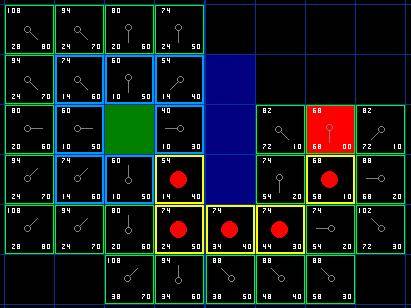
蓝色框框表示在Close表中，绿色的框框表示在Open表中

最后回溯得到路径

三、代码实现(Java)

1. 输入

(1) 代表地图二值二维数组(0表示可通路，1表示路障)

int[][] maps = {{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },{ 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 },{ 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0 },{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }};

(2) 按照二维数组的特点，坐标原点在左上角，所以y是高，x是宽，y向下递增，x向右递增，我们将x和y封装成一个类，好传参，重写equals方法比较坐标(x,y)是不是同一个。

public class Coord
{public int x;public int y;public Coord(int x, int y){this.x = x;this.y = y;}@Overridepublic boolean equals(Object obj){if (obj == null) return false;if (obj instanceof Coord){Coord c = (Coord) obj;return x == c.x && y == c.y;}return false;}
}

(3) 封装路径结点类，字段包括：坐标、G值、F值、父结点，实现Comparable接口，方便优先队列排序。

public class Node implements Comparable<Node>
{public Coord coord; // 坐标public Node parent; // 父结点public int G; // G：是个准确的值，是起点到当前结点的代价public int H; // H：是个估值，当前结点到目的结点的估计代价public Node(int x, int y){this.coord = new Coord(x, y);}public Node(Coord coord, Node parent, int g, int h){this.coord = coord;this.parent = parent;G = g;H = h;}@Overridepublic int compareTo(Node o){if (o == null) return -1;if (G + H > o.G + o.H)return 1;else if (G + H < o.G + o.H) return -1;return 0;}
}

(4) 最后一个数据结构是A星算法输入的所有数据，封装在一起，传参方便。😁

public class MapInfo
{public int[][] maps; // 二维数组的地图public int width; // 地图的宽public int hight; // 地图的高public Node start; // 起始结点public Node end; // 最终结点public MapInfo(int[][] maps, int width, int hight, Node start, Node end){this.maps = maps;this.width = width;this.hight = hight;this.start = start;this.end = end;}
}

2. 处理

(1) 在算法里需要定义几个常量来确定：二维数组中哪个值表示障碍物、二维数组中绘制路径的代表值、计算G值需要的横纵移动代价和斜移动代价。

    public final static int BAR = 1; // 障碍值public final static int PATH = 2; // 路径public final static int DIRECT_VALUE = 10; // 横竖移动代价public final static int OBLIQUE_VALUE = 14; // 斜移动代价

(2) 定义两个辅助表：Open表和Close表。Open表的使用是需要取最小值，在这里我们使用Java工具包中的优先队列PriorityQueue，Close只是用来保存结点，没其他特殊用途，就用ArrayList。

    Queue<Node> openList = new PriorityQueue<Node>(); // 优先队列(升序)List<Node> closeList = new ArrayList<Node>();

(3) 定义几个布尔判断方法：最终结点的判断、结点能否加入open表的判断、结点是否在Close表中的判断。

    /*** 判断结点是否是最终结点*/private boolean isEndNode(Coord end,Coord coord){return coord != null && end.equals(coord);}/*** 判断结点能否放入Open列表*/private boolean canAddNodeToOpen(MapInfo mapInfo,int x, int y){// 是否在地图中if (x < 0 || x >= mapInfo.width || y < 0 || y >= mapInfo.hight) return false;// 判断是否是不可通过的结点if (mapInfo.maps[y][x] == BAR) return false;// 判断结点是否存在close表if (isCoordInClose(x, y)) return false;return true;}/*** 判断坐标是否在close表中*/private boolean isCoordInClose(Coord coord){return coord!=null&&isCoordInClose(coord.x, coord.y);}/*** 判断坐标是否在close表中*/private boolean isCoordInClose(int x, int y){if (closeList.isEmpty()) return false;for (Node node : closeList){if (node.coord.x == x && node.coord.y == y){return true;}}return false;}

(4) 计算H值，“曼哈顿” 法，坐标分别取差值相加

private int calcH(Coord end,Coord coord)
{return Math.abs(end.x - coord.x) + Math.abs(end.y - coord.y);
}

(5) 从Open列表中查找结点

private Node findNodeInOpen(Coord coord)
{if (coord == null || openList.isEmpty()) return null;for (Node node : openList){if (node.coord.equals(coord)){return node;}}return null;
}

(6) 添加邻结点到Open表

/*** 添加所有邻结点到open表*/
private void addNeighborNodeInOpen(MapInfo mapInfo,Node current)
{int x = current.coord.x;int y = current.coord.y;// 左addNeighborNodeInOpen(mapInfo,current, x - 1, y, DIRECT_VALUE);// 上addNeighborNodeInOpen(mapInfo,current, x, y - 1, DIRECT_VALUE);// 右addNeighborNodeInOpen(mapInfo,current, x + 1, y, DIRECT_VALUE);// 下addNeighborNodeInOpen(mapInfo,current, x, y + 1, DIRECT_VALUE);// 左上addNeighborNodeInOpen(mapInfo,current, x - 1, y - 1, OBLIQUE_VALUE);// 右上addNeighborNodeInOpen(mapInfo,current, x + 1, y - 1, OBLIQUE_VALUE);// 右下addNeighborNodeInOpen(mapInfo,current, x + 1, y + 1, OBLIQUE_VALUE);// 左下addNeighborNodeInOpen(mapInfo,current, x - 1, y + 1, OBLIQUE_VALUE);
}/*** 添加一个邻结点到open表*/
private void addNeighborNodeInOpen(MapInfo mapInfo,Node current, int x, int y, int value)
{if (canAddNodeToOpen(mapInfo,x, y)){Node end=mapInfo.end;Coord coord = new Coord(x, y);int G = current.G + value; // 计算邻结点的G值Node child = findNodeInOpen(coord);if (child == null){int H=calcH(end.coord,coord); // 计算H值if(isEndNode(end.coord,coord)){child=end;child.parent=current;child.G=G;child.H=H;}else{child = new Node(coord, current, G, H);}openList.add(child);}else if (child.G > G){child.G = G;child.parent = current;// 重新调整堆openList.add(child);}}
}

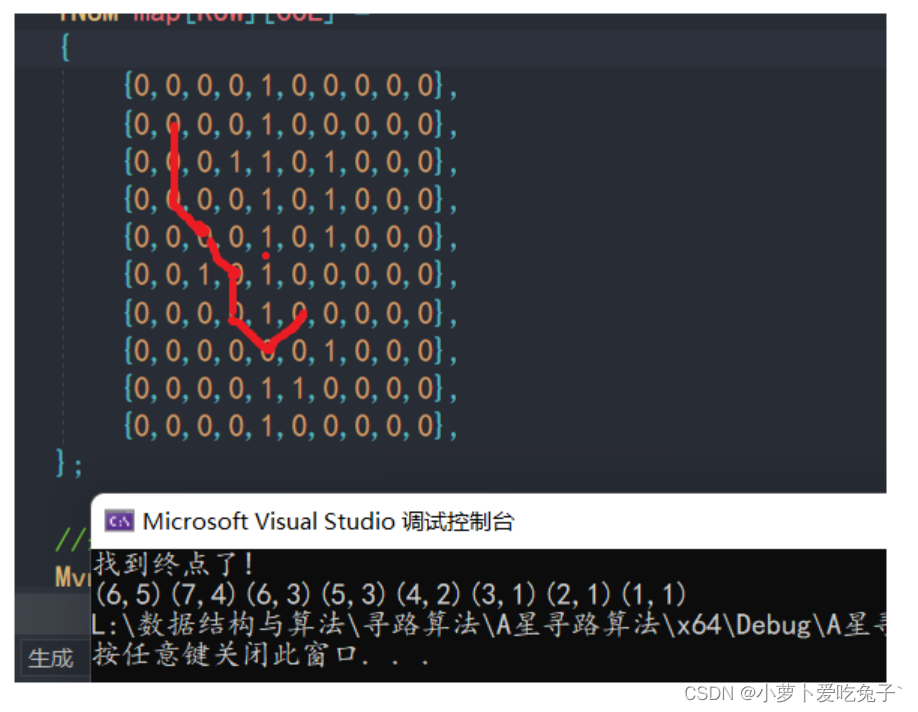
(7) 回溯法绘制路径

private void drawPath(int[][] maps, Node end)
{if(end==null||maps==null) return;System.out.println("总代价：" + end.G);while (end != null){Coord c = end.coord;maps[c.y][c.x] = PATH;end = end.parent;}
}

(8) 开始算法，循环移动结点寻找路径，设定循环结束条件，Open表为空或者最终结点在Close表


public void start(MapInfo mapInfo)
{if(mapInfo==null) return;// cleanopenList.clear();closeList.clear();// 开始搜索openList.add(mapInfo.start);moveNodes(mapInfo);
}/*** 移动当前结点*/
private void moveNodes(MapInfo mapInfo)
{while (!openList.isEmpty()){Node current = openList.poll();closeList.add(current);addNeighborNodeInOpen(mapInfo,current);if (isCoordInClose(mapInfo.end.coord)) // bug修正{drawPath(mapInfo.maps, mapInfo.end);break;}}
}

附：源码地址：点击这里


http://chatgpt.dhexx.cn/article/oHsMCTjl.shtml

相关文章

A-Star（A*）算法

A-Star（A*）算法

【由于专栏后几篇限制vip观看&#xff0c;我又把完整算法在公众号“武汉AI算法研习”进行了发布&#xff0c;可以查看全专栏文章。】 A-Star(A*)算法作为Dijkstra算法的扩展&#xff0c;在寻路和图的遍历过程中具有一定的高效性。 【适用范围】静态图搜索 【算法流程】A-Sta…
阅读更多...
A星算法代码

A星算法代码

A星算法代码python3实现 前言一、A*&#xff1f; A星1.一个搜索算法2.结果展示 二、使用环境1.python 3.x2.一些解释说明 一些话 前言 产生本文的缘由 学校计科课程要求的小作业, 在csdn上看了好多, 记录一下自己的学习 以下是本篇文章正文内容 一、A*&#xff1f; A星 1.一…
阅读更多...
A星算法(基于matlab)

A星算法(基于matlab)

概述 基于上一篇文章提到的DFS算法和BFS算法 A星算法属于图这种数据结构的搜索算法&#xff0c;对比于树的遍历搜索&#xff0c;需要考虑到的问题是&#xff1a;同一个节点的重复访问&#xff0c;所以需要对于已经访问过的节点进行标记。 曼哈顿距离&#xff1a; 在几何度量空…
阅读更多...
【A星算法】--第四篇（A星算法）

【A星算法】--第四篇（A星算法）

本篇主要介绍A星算法的过程&#xff1a; * 把起始节点加进openList * while openList 不为空 { * 当前节点 openList 中成本最低的节点 * if&#xff08;当前节点 目标节点&#xff09;{ * 路径完成 …
阅读更多...
A星算法详解(个人认为最详细,最通俗易懂的一个版本)

A星算法详解(个人认为最详细,最通俗易懂的一个版本)

A* 寻路算法 原文地址&#xff1a; http://www.gamedev.net/reference/articles/article2003.asp 概述 虽然掌握了 A* 算法的人认为它容易&#xff0c;但是对于初学者来说&#xff0c; A* 算法还是很复杂的。 搜索区域(The Search Area) 我们假设某人要从 A 点移动到 B 点&…
阅读更多...
A星算法理解

A星算法理解

A星算法理解 1.选择A星算法的原因 为了进行路径规划算法是不可回避的&#xff1a;启发式搜索算法是比较常规的一类算法就是在状态空间中的搜索对每一个搜索的位置进行评估&#xff0c;得到最好的位置&#xff0c;再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路…
阅读更多...
A星(A*, A Star)算法详解

A星(A*, A Star)算法详解

MulinB按&#xff1a;经典的智能寻路算法&#xff0c;一个老外写的很透彻很清晰&#xff0c;很容易让人理解神秘的A*算法。以下是一个中文翻译版。 A*寻路初探 GameDev.net 作者&#xff1a; Patrick Lester 译者&#xff1a;Panic 2005年3月18日 译者序&#xff1a;很久以前就…
阅读更多...
A星算法

A星算法

A星算法 1.简述 A星算法就是试图在地图中找到一条最短路径&#xff0c;但不保证一定存在。 任务 小猫去找青蛙玩&#xff08;好TM弱智啊~&#xff09;条件 黑色方块无法通行&#xff0c;每走一个格子小猫消耗的体力都为1。 2.如果说你是小猫&#xff0c;你会怎么走&#xf…
阅读更多...
A星算法说明

A星算法说明

A*算法说明 文章目录 前言原理说明如何构造 h ( n ) h(n) h(n)一、欧氏距离二、曼哈顿距离三、其他 关于 g ( n ) g(n) g(n)路况设置如何实现 完整的流程搜索过程图示允许斜走&#xff0c;使用优先队列禁止斜走&#xff0c;使用优先队列允许斜走&#xff0c;使用普通队列禁止斜…
阅读更多...
A星算法优化（一）启发函数

A星算法优化（一）启发函数

基于Python语言对A星算法进行优化&#xff1a;(视频中会拿python与matlab作对比) 源码地址&#xff1a;https://github.com/Grizi-ju/ros_program/blob/main/path_planning/Astar.py B站详解视频&#xff1a;https://www.bilibili.com/video/BV1FL4y1M7PM?spm_id_from333.999…
阅读更多...
猴子都能看懂的A星算法原理

猴子都能看懂的A星算法原理

文章目录 A星算法基本原理什么是寻路算法算法的思路 算法实现脚本1————cconst.cs脚本2————AStar.cs Unity演示演示样例一演示样例二演示样例三演示样例四 俗话说&#xff0c;好记性不如烂笔头&#xff0c;对于有了解过寻路算法的同学&#xff0c;对于A星算法应该不陌生…
阅读更多...
A星寻路算法详解（C++实现 完整代码+图片演示 ）

A星寻路算法详解（C++实现 完整代码+图片演示 ）

文章目录 三种寻路算法 A星寻路算法A星寻路算法思想A星寻路准备A星寻路过程&#xff08;图例&#xff09;A星寻路代码&#xff08;完整&#xff09; 三种寻路算法 深度寻路算法&#xff1a;不一定能找到最佳路径&#xff0c;但是寻路快速&#xff0c;只能走直线。广度寻路算法…
阅读更多...
A星(A*、A Star)路径规划算法详解（附MATLAB代码）

A星(A*、A Star)路径规划算法详解（附MATLAB代码）

首先看看运行效果&#xff0c;分别有三种模式&#xff0c;代码运行前需要通过鼠标点击设置起点和终点。 第一种模式直接输出最短路径 第二种模式输出最短路径的生成过程 第三种模式输出最短路径的生成过程和详细探索的过程 代码获取 gitee链接&#xff1a;https://gitee.c…
阅读更多...
什么是脏读？不可重复读？幻读？如何解决？

什么是脏读？不可重复读？幻读？如何解决？

什么是脏读&#xff1f;不可重复读&#xff1f;幻读&#xff1f;如何解决&#xff1f; 朋友最近面试美团&#xff0c;被面试官问到数据库的幻读问题&#xff0c;自己正好最近复习到这&#xff0c;做个笔记整理一下数据库的三大特征以及隔离级别。 一.先来回顾一下什么是事务&…
阅读更多...
MySQL理论：脏读、不可重复读、幻读

MySQL理论：脏读、不可重复读、幻读

&#x1f3c6;今日学习目标&#xff1a; &#x1f340;MySQL理论&#xff1a;脏读、不可重复读、幻读 ✅创作者&#xff1a;林在闪闪发光 ⏰预计时间&#xff1a;30分钟 &#x1f389;个人主页&#xff1a;林在闪闪发光的个人主页 &#x1f341;林在闪闪发光的个人社区&#xf…
阅读更多...
数据库事务隔离级别（脏读、幻读、不可重复读）

数据库事务隔离级别（脏读、幻读、不可重复读）

一、脏读、幻读和不可重复读 一、脏读、不可重复读、幻读 1、脏读&#xff1a;脏读就是指当一个事务正在访问数据&#xff0c;并且对数据进行了修改&#xff0c;而这种修改还没有提交到数据库中&#xff0c;这时&#xff0c;另外一个事务也访问这个数据&#xff0c;然后使用了…
阅读更多...
快速理解脏读，不可重复读，幻读

快速理解脏读，不可重复读，幻读

介绍 要聊事务&#xff0c;不可避免的要提到数据库事务的四大特性&#xff1a;ACID atomicconsistenceisolationdurability 先放一个表格&#xff0c;看看4个隔离级别会出现的各种问题&#xff0c;网上的解释一大堆。看完后还是一脸懵逼&#xff0c;感觉懂了&#xff0c;又好…
阅读更多...
MySQL之脏写、脏读、不可重复读、幻读

MySQL之脏写、脏读、不可重复读、幻读

脏写和脏读都是在多个事务同时修改或读取同一行数据的情况下产生的问题。比如现在有事务1和事务2同时对一行数据进行修改&#xff0c;事务1将值改成1&#xff0c;而事务2将值改成了2&#xff0c;这时的值应该是2&#xff0c;但是就在这时&#xff0c;事务1发生了回滚&#xff0…
阅读更多...
数据库必备知识：脏读和幻读的定义及应对策略

数据库必备知识：脏读和幻读的定义及应对策略

随着数据库应用的广泛使用&#xff0c;数据库并发性和一致性的问题成为了引起重视的问题之一。其中&#xff0c;脏读&#xff08;Dirty Read&#xff09;和幻读&#xff08;Phantom Read&#xff09;是常见的并发访问问题&#xff0c;本文将对脏读、幻读进行详细介绍&#xff0…
阅读更多...
Seata AT模式怎样防止脏写和脏读

Seata AT模式怎样防止脏写和脏读

前言 Seata AT 模式是一种非侵入式的分布式事务解决方案&#xff0c;Seata 在内部做了对数据库操作的代理层&#xff0c;我们使用 Seata AT 模式时&#xff0c;实际上用的是 Seata 自带的数据源代理 DataSourceProxy&#xff0c;Seata 在这层代理中加入了很多逻辑&#xff0c;…
阅读更多...
推荐文章

Copyright @ 2022~2023