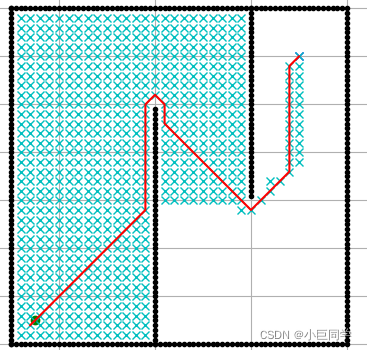
本篇主要介绍A星算法的过程:
* 把起始节点加进openList
* while openList 不为空 {
* 当前节点 = openList 中成本最低的节点
* if(当前节点 = 目标节点){
* 路径完成
* }else{
* 把当前节点移入closeedList
* 检查当前节点的每个相邻节点
* for 每一个相邻节点
* if(该节点不在openList && 该节点不在closedList中 && 该节点不是障碍物){
* 讲该节点放进openlist并且计算成本;
* }
* }
* }
本篇中用到的工具函数,计算两个节点的距离:
注:magnitude 返回向量的长度(只读)
magnitude 的计算向:量的长度是(x*x+y*y+z*z)的平方根。
如果需要仅需比较长度的,可以比较它们长度的平方,使用sqrMagnitude(计算平方很快)。
private static float NodeCost(Node a, Node b){Vector3 vecCost = a.postion - b.postion;return vecCost.magnitude;}下面是A星寻路的方法,方法可以放在Update中不断调用,建议是计时器调用:
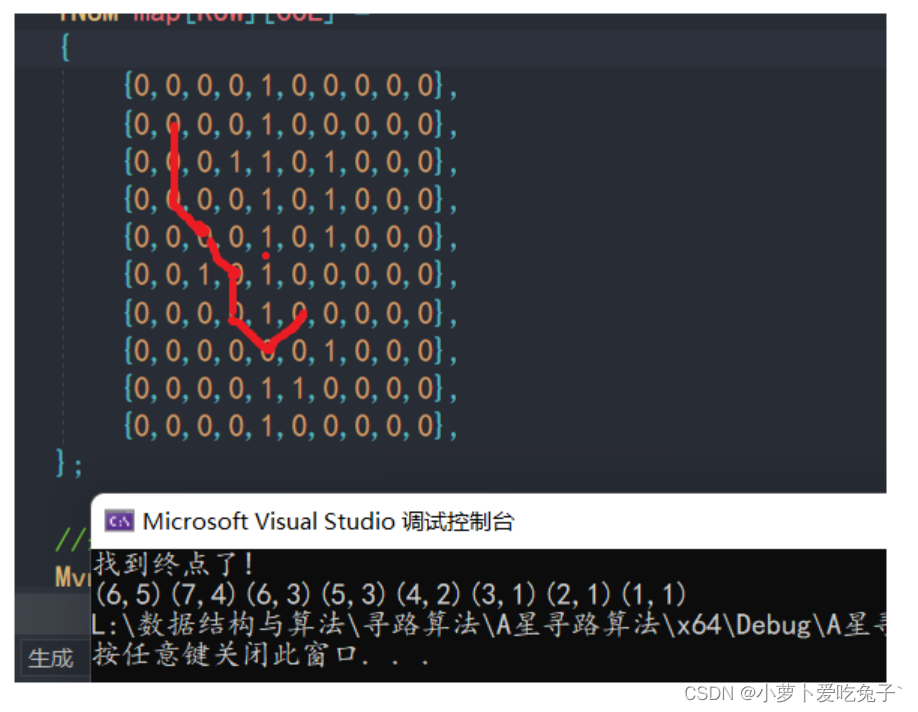
public static ArrayList FindPath(Node start, Node goal){openList = new PriorityQueue();openList.Push(start);start.nodeTotalCost = 0.0f;start.estimatedCost = NodeCost(start, goal);closeList = new PriorityQueue();Node node = null;while (openList.Length != 0){node = openList.FirstNode();if (node.postion == goal.postion){return CalculatePath(node);}ArrayList neighbours = new ArrayList();GridManager.instance.GetNeigighbours(node, neighbours);for (int i = 0; i < neighbours.Count; i++){Node neighbour = (Node)neighbours[i];if (!closeList.Contains(neighbour)){float cost = NodeCost(node, neighbour);float totalCost = node.nodeTotalCost + cost;float neighbourNodeEst = NodeCost(neighbour, goal);neighbour.nodeTotalCost = totalCost;neighbour.estimatedCost = totalCost + neighbourNodeEst;neighbour.parent = node;if (!openList.Contains(neighbour)){openList.Push(neighbour);}}}closeList.Push(node);openList.Remove(node);}if (node.postion != goal.postion){Debug.LogError("Goal Not Found");return null;}return CalculatePath(node);}private static ArrayList CalculatePath(Node node){ArrayList list = new ArrayList();while (node != null){if (node.parent != null){list.Add(node.parent);}node = node.parent;}list.Reverse();return list; }


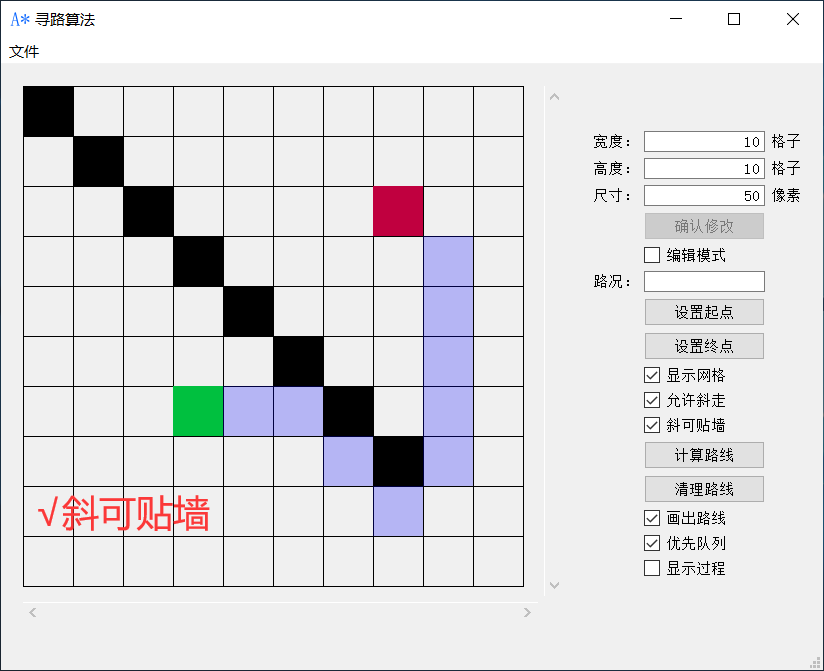


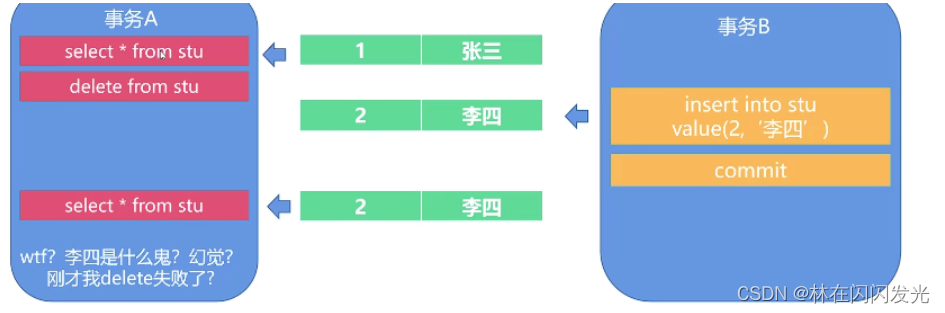





![[Database] 脏读、幻读这些都是什么?事务隔离级别又是什么?MySQL数据库的事务隔离级别都有哪些?](https://img-blog.csdnimg.cn/0b42b3bc46874658a5c93fe5e8c41c09.png)