文章目录
- 三种寻路算法
- A星寻路算法
- A星寻路算法思想
- A星寻路准备
- A星寻路过程(图例)
- A星寻路代码(完整)
三种寻路算法
- 深度寻路算法:不一定能找到最佳路径,但是寻路快速,只能走直线。
- 广度寻路算法:一定能找到最短路径,但是开销大,时间慢,只能走直线。
- A星寻路算法(常用):一定能找到最短路径,可以走直线和斜线,而且开销较小,常用于大型地图的寻路
A星寻路算法
A星寻路算法思想
引入: 狼吃羊模型。
狼捕猎羊:如果抓到了就加100分;如果狼不动,每分钟减2分;如果狼抓捕时会跑,跑步每分钟减5分;
狼会饿 ,饿的时候每分钟减10分。 有一个积分的概念在这里面。结果会发现狼会站在原地不动。
因为狼直到,抓住羊很困难,跑步时会扣分,饿时会扣分,不动时也会扣分。但是人工智能狼计算出了站着不动时扣分的代价最低,而干其他事代价都高,因此狼会自动选择代价最低的方式,一动不动
之后又加了设定:原地不动每分钟也扣分,而且是线性扣分。结果你会发现狼从一开始就会自杀。
同理,自杀是代价最小的选择(即分数最高,如果你干其他的事,则可能会负分,所以狼会选择自杀)。
A星寻路算法也引入了这一概念,即通过计算和量化行走的各个方向的代价,来选择最优路径
- 公式: f = g + h
- f: 设定其为最终评估代价
- g:当前点走到下一点的付出的代价
- h:当前点到终点的预期代价
- 通过比较各条路线的最终代价,选择最小代价,即为合适的路径,也为最短路径。
A星寻路准备
地图行列数,方向枚举,地图,辅助地图的设计等在此不描述,具体请看之前我写的前两种寻路算法的博客。
广度寻路算法
深度寻路算法
- 记录坐标点的类型,GetH和GetF函数即为计算各种代价的函数,稍后会介绍。一个重载用来比较当前点是否到达终点
h表示当前点到终点的预期代价,因此我们每次移动一步,都需要求出 h,而h的计算我们可以直接通过数格子来获得,即水平,竖直个有几个格子,这便是预期的代价
g表示走到每一点的代价,因此每走一个方向,记录这个方向的代价, 最后选择代价最小的方向即可,g可以通过遍历八个方向来记录
f =g + h
//点类型
struct Mypoint
{int row;int col;int f, g, h;bool operator==(const Mypoint& pos){return (pos.row == row && pos.col == col);}void GetH(const Mypoint& Begpos, const Mypoint& Endpos){int x = abs(Begpos.col - Endpos.col);//计算水平差距int y = abs(Begpos.row - Endpos.row);//计算垂直差距h = x + y;//计算总的差距}inline void GetF(){f = g + h;//计算f}
};
- 存储位置节点的树结构,含有构造函数用来构建树节点,vector数组存储多个节点:因为一个父亲会有多个孩子的情况。
//树结构存储节点
struct TreeNode
{Mypoint pos;//当前点坐标TreeNode* pParent;//当前点的父节点vector<TreeNode*> pChild; //存储当前点的所有孩子节点//构造函数TreeNode(const Mypoint& pos){this->pos = pos;pParent = nullptr;}
};- 判断是否能走的函数,用于判断地图某个点是否能走,即不为墙,没越界,没走过,则能走。
//判断某个点能否走
bool CanWalk(int map[ROW][COL], bool vis[ROW][COL], const Mypoint& pos)
{//如果越界,不能走if (pos.row < 0 || pos.col < 0 || pos.row >= ROW || pos.col >= COL){return false;}//如果是墙,不能走if (map[pos.row][pos.col]){return false;}//如果已经走过,不能走if (vis[pos.row][pos.col]){return false;}return true;//否则能走
}
- 数据的准备
- 起点与终点的坐标
- 树根节点,用于保存寻路的树结构
- buff数组来记录每一个孩子节点,用来确定下一步该走的点
- vis标记数组,不能重复走
- 当前点与试探点
void init()
{//地图,1表示墙,0表示路径int map[ROW][COL] ={{0,0,0,0,1,0,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},{0,0,0,1,1,0,1,0,0,0},{0,0,0,0,1,0,1,0,0,0},{0,0,0,0,1,0,1,0,0,0},{0,0,1,0,1,0,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,0,1,0,0,0},{0,0,0,0,1,1,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},};//起始点和终点Mypoint Begpos = { 1,1 };Mypoint Endpos = { 6,5 };//标记有没有走过bool vis[ROW][COL] = { false };//创建树根,即根节点TreeNode* pRoot = new TreeNode(Begpos);vector<TreeNode*> buff; //存储孩子节点的数组TreeNode* pCurrent = pRoot; //记录当前点TreeNode* pTemp = nullptr; //试探节点,用于试探下一个位置的点bool isFindEnd = false;//终点标记
}
A星寻路过程(图例)
假定直着走的代价为10,斜着走的代价为14
-
首先计算起点位置周围八个方向付出代价(蓝色),此代价为付出的代价 g。
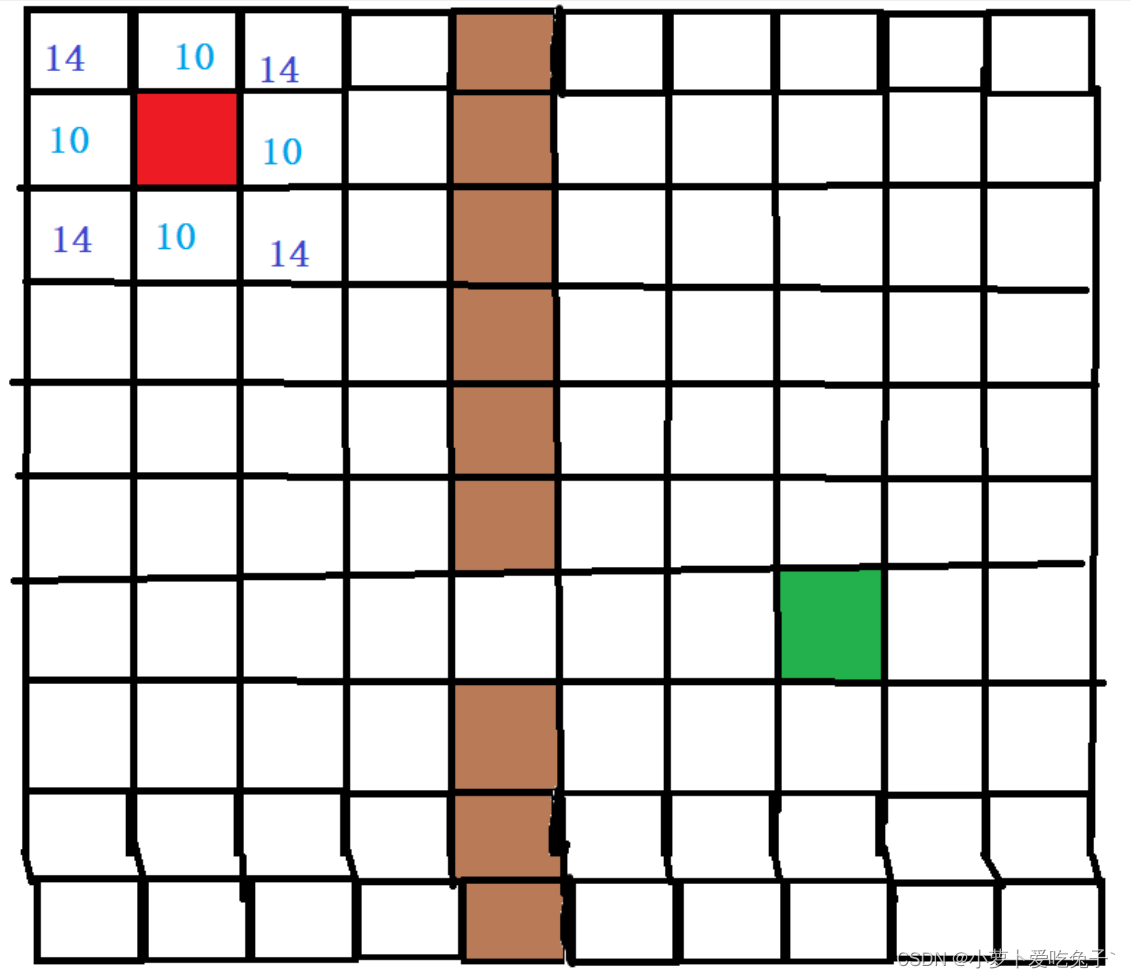
-
然后再计算起点到终点的代价(如何计算:数格子即可,某个点到终点的格子数,只能行列,不能斜着),此代价为预期代价h,可以发现 最终代价=付出+预期,可以得到一个最小的代价点,即右下角的斜着的点。
这个点即是我们下一步要走的点。依次类推,在下个点上,再次计算周围代价最小的点,然后再次移动
upd: 2023. 2.22 新增一个图
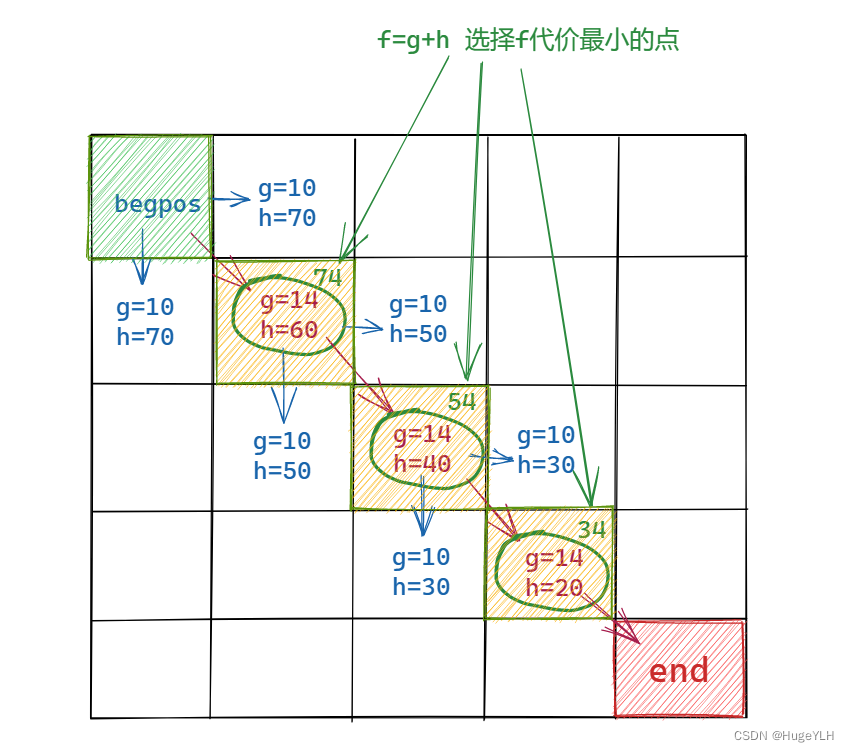
-
注意:标记起始点和每个移动到的点为已经走过点,即下一次不会重复移动到这个点。
-
在移动到的点处(代价最小点),继续遍历八个方向,除了墙壁和已经走过点,继续计算最终代价,找到最终代价小的点,移动。
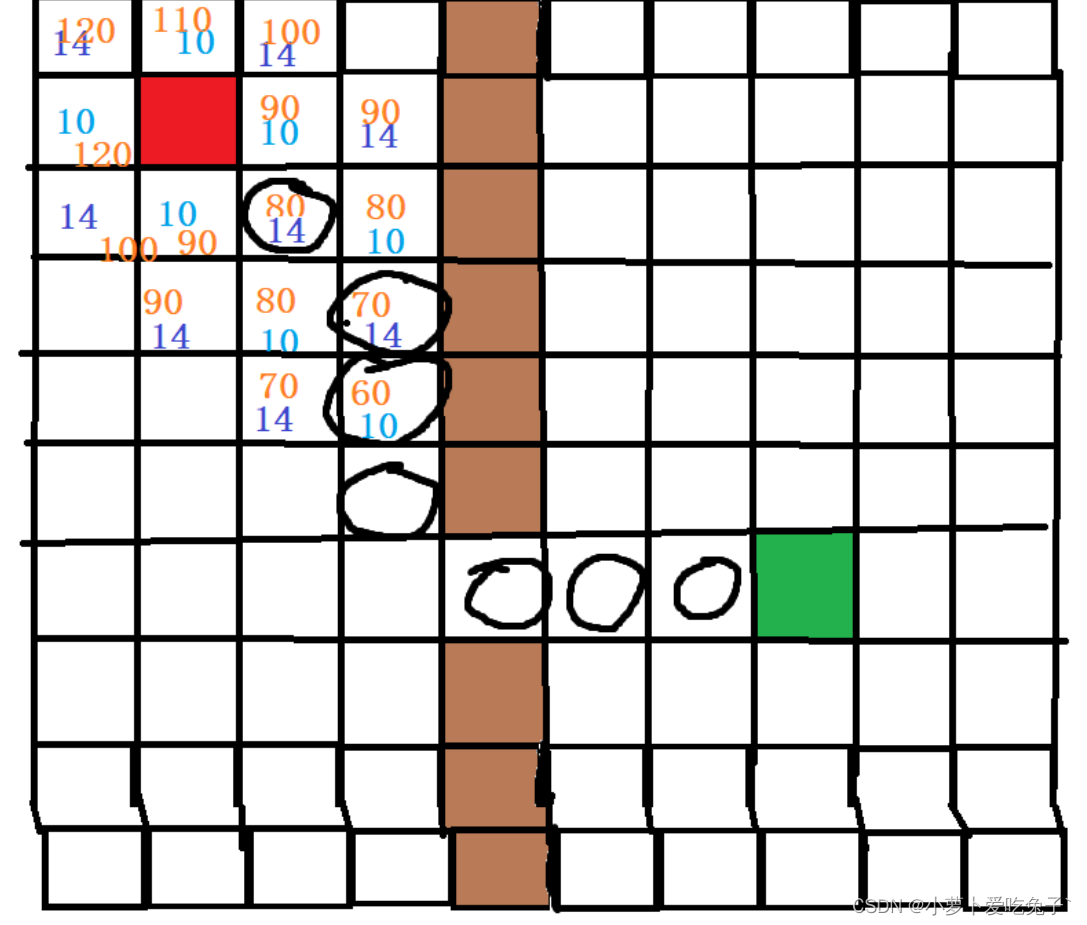
-
注意:如果你移动到了一个死胡同,则必须回退,如何回退?
我们事先准备了一个容器vector名字叫做 buff ,来存储我们每次遍历的方向的节点,即我们把每一个方向都创建一个节点,然后节点入树,节点再入容器,当我们走到死胡同时,通过找到容器内的最小元素(即是代价最小点,但是这个点是死胡同),然后把他删除,则 再次找一个代价最小点,然后移动到它那里去 。
如果地图没有终点,则可以想到,容器会一直删除,然后为空,此时则退出,没有终点。
A星寻路代码(完整)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;const int ROW = 10;
const int COL = 10;
const int ZXDJ = 10; //直线代价
const int XXDJ = 14; //斜线代价
enum Dir { p_up, p_down, p_left, p_right, p_lup, p_ldown, p_rup, p_rdown };
struct Mypoint
{int row;int col;int f, g, h;bool operator==(const Mypoint& pos){return (pos.row == row && pos.col == col);}void GetH(const Mypoint& Begpos, const Mypoint& Endpos){int x = abs(Begpos.col - Endpos.col);//计算水平差距int y = abs(Begpos.row - Endpos.row);//计算垂直差距h = x + y;//计算总的差距}inline void GetF(){f = g + h;//计算f}
};//树结构存储节点
struct TreeNode
{Mypoint pos;//当前点坐标TreeNode* pParent;//当前点的父节点vector<TreeNode*> pChild; //存储当前点的所有孩子节点//构造函数TreeNode(const Mypoint& pos){this->pos = pos;pParent = nullptr;}
};//判断某个点能否走
bool CanWalk(int map[ROW][COL], bool vis[ROW][COL], const Mypoint& pos)
{//如果越界,不能走if (pos.row < 0 || pos.col < 0 || pos.row >= ROW || pos.col >= COL){return false;}//如果是墙,不能走if (map[pos.row][pos.col]){return false;}//如果已经走过,不能走if (vis[pos.row][pos.col]){return false;}return true;//否则能走
}int main()
{//地图,1表示墙,0表示路径int map[ROW][COL] ={{0,0,0,0,1,0,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},{0,0,0,1,1,0,1,0,0,0},{0,0,0,0,1,0,1,0,0,0},{0,0,0,0,1,0,1,0,0,0},{0,0,1,0,1,0,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},{0,0,0,0,0,0,1,0,0,0},{0,0,0,0,1,1,0,0,0,0},{0,0,0,0,1,0,0,0,0,0},};//起始点和终点Mypoint Begpos = { 1,1 };Mypoint Endpos = { 6,5 };//标记有没有走过bool vis[ROW][COL] = { false };//创建树根,即根节点TreeNode* pRoot = new TreeNode(Begpos);vector<TreeNode*> buff; //存储孩子节点的数组TreeNode* pCurrent = pRoot; //记录当前点TreeNode* pTemp = nullptr; //试探节点,用于试探下一个位置的点bool isFindEnd = false;//终点标记//开始寻路while (1){//1. 某个点八个方向依次遍历 计算g代价for (int i = 0; i < 8; ++i){//确定试探点的属性pTemp = new TreeNode(pCurrent->pos);//八个方向进行试探!switch (i){//直线代价case p_up://上pTemp->pos.row--;pTemp->pos.g += ZXDJ;break;case p_down://下pTemp->pos.row++;pTemp->pos.g += ZXDJ;break;case p_left://左pTemp->pos.col--;pTemp->pos.g += ZXDJ;break;case p_right://右pTemp->pos.col++;pTemp->pos.g += ZXDJ;break;//斜线代价case p_lup://左上pTemp->pos.row--;pTemp->pos.col--;pTemp->pos.g += XXDJ;break;case p_ldown://左下pTemp->pos.row++;pTemp->pos.col--;pTemp->pos.g += XXDJ;break;case p_rup://右上pTemp->pos.row--;pTemp->pos.col++;pTemp->pos.g += XXDJ;break;case p_rdown://右下pTemp->pos.row++;pTemp->pos.col++;pTemp->pos.g += XXDJ;break;}//判断他们能不能走,能走的计算h及f 入树 存储在buff数组if (CanWalk(map, vis, pTemp->pos)){ //能走//计算代价pTemp->pos.GetH(pTemp->pos, Endpos);//计算h代价pTemp->pos.GetF();//得到最后的f代价,f=g+h //把能走的这个点存入树中pCurrent->pChild.push_back(pTemp);//pTemp表示的就是下一个能走的点pTemp->pParent = pCurrent;//父子关系确定//存入数组buff.push_back(pTemp);//标记这个点走过vis[pTemp->pos.row][pTemp->pos.col] = true;}else{//不能走则删除pTemp,继续遍历下一个方向的点delete pTemp;pTemp = nullptr;}}/*遍历完八个方向后,找到最小代价点,并且移动,然后删除*/auto itMin = min_element(buff.begin(), buff.end(), [&](TreeNode* p1, TreeNode* p2){return p1->pos.f < p2->pos.f;});//当前点移动到这个最小代价点pCurrent = *itMin;//删除最小代价节点buff.erase(itMin);//有没有到达终点if (pCurrent->pos == Endpos){isFindEnd = true;break;}//没有终点,自然一直删除节点,则buff为空if (buff.size() == 0){break;}}if (isFindEnd){cout << "找到终点了!\n";while (pCurrent){cout << "(" << pCurrent->pos.row << "," << pCurrent->pos.col << ")";pCurrent = pCurrent->pParent;}}else{cout << "没有找到终点!\n";}return 0;
}
终点row,col(7,7):

终点row,col(6,5)
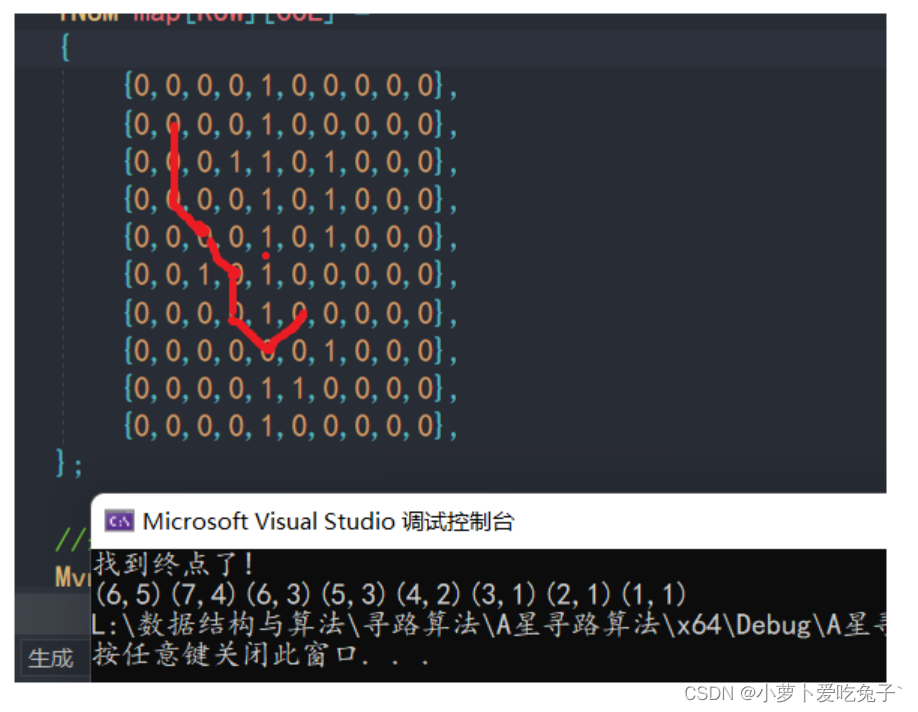






![[Database] 脏读、幻读这些都是什么?事务隔离级别又是什么?MySQL数据库的事务隔离级别都有哪些?](https://img-blog.csdnimg.cn/0b42b3bc46874658a5c93fe5e8c41c09.png)