A-star算法自学

article/2025/10/2 20:19:48

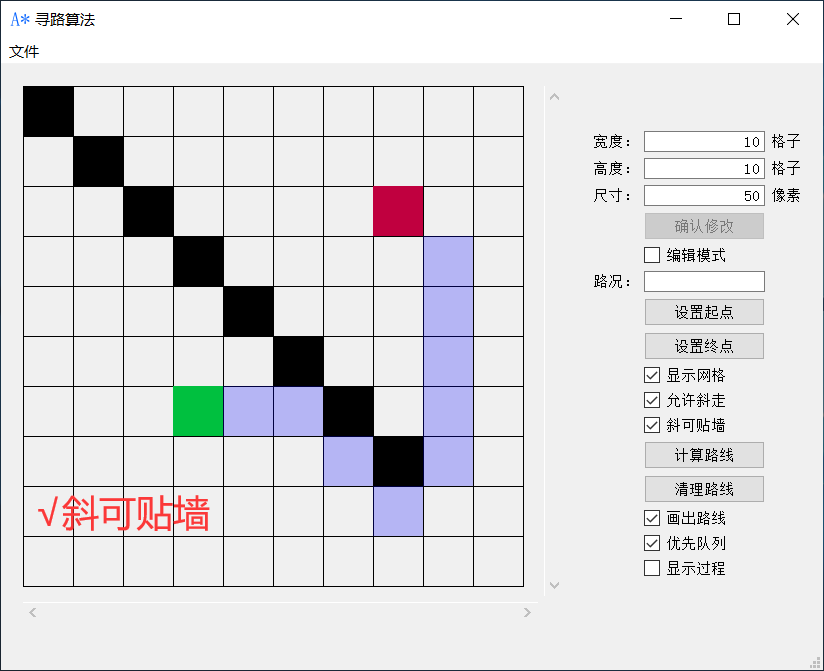
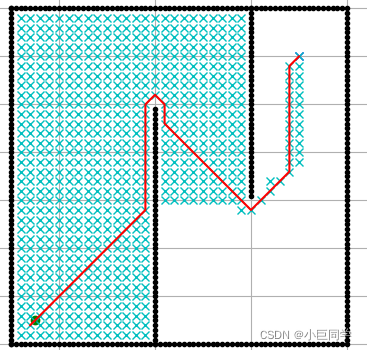
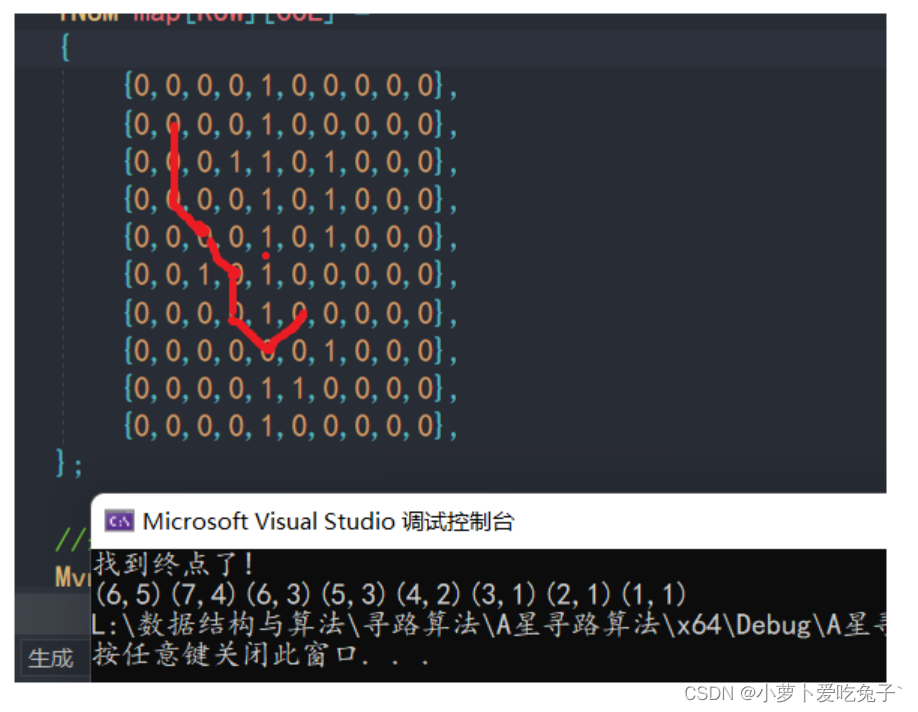
搜索过程

广度优先搜索（BFS）算法与Dijsktra算法的结合，可以得出最短的路径。
将地图信息通过划分为方形或者其他多边形格子的方法进行表示，便于利用二维数组存放地图信息，每个格子有可行和不可行两种状态；每个方格用节点的形式表示（节点可以放置在形状内的任何位置 - 在中心或沿边缘），以便于用于任何形状的格子中的情况。
如上图所示，绿色格子为起点，红色格子为终点，蓝色格子为障碍物
如上图所示，绿色格子为起点，红色格子为终点，蓝色格子为障碍物

评价函数

移动代价
横向/纵向移动代价设为 10
对角线移动代价设为14
主要计算三个值F、G及H
F = G + H
F：从初始块经由n个块后到目标块的最小代价估计
G：表示从起点s到点n的实际成本
G(s) = G(s的父节点) + 10或14(横向移动或者纵向移动)
H：表示从节点n到目标T的估算成本（试探法）
利用曼哈顿方法计算: 计算当前方格n通过横向或者纵向移动到T的节点数 * 10
d = |x1 - x2| + |y1 - y2| * 10
欧式距离计算: 计算n与T的欧式距离

步骤(参考)

设置一个 open list（待检查列表） 及 close list（无需检查列表）

  1. 从起点开始，将其存入open list中，open list中的方格可能是路径会通过的，也可能是路径不会通过的方格。

  2. 寻找起点周围所有可以到达的节点（相邻节点），忽略障碍方格；并将这些相邻节点存入open list中并且这些节点的父节点均为起点。

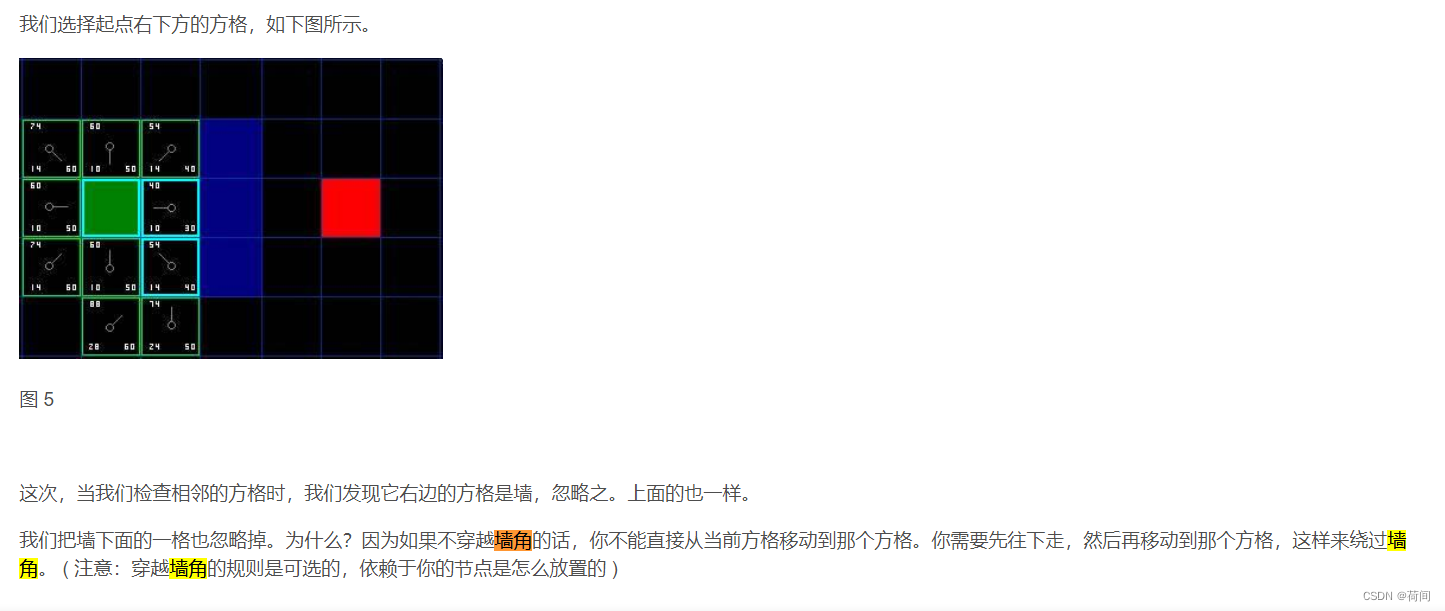
  3. 从open list中将起点取出，存入 close list中，如下图所示：![[Pasted image 20230426120659.png]]图中绿色方块为起点，其边框为蓝色，表示该方块已存入close list中，并且其周围的8个方块均在open list中，且指针指向中间的绿色方块，表示父节点为绿色方块

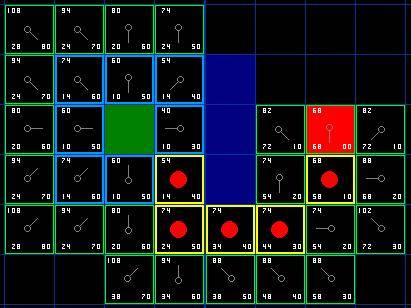
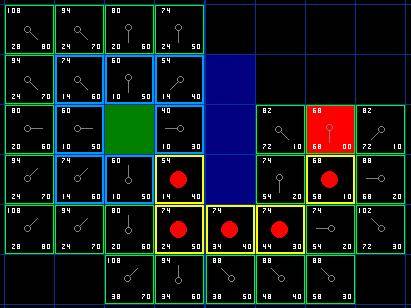
  4. 继续遍历open list中的节点，并重复下述过程。

    1. 计算每个节点的F值，选择F值的节点n作为当前处理的节点
    2. 对于当前节点n，与其相邻的所有节点（b，c，d等）如下操作：
      1. 如果节点b是不可到达（unreachable）或者在close list中，则不进行任务操作
      2. 如果节点c不在open list中，则将其加入open list中，并将当前节点n设为c 的父代，计算节点b的F、G、H值
      3. 若节点d在open list中，则检查节点n到节点d的路径是否更优（若该路径的g值更小，则说明其更优）；若该路径更优，则将节点d的父节点（假设为e）设置为当前节点，并重新计算节点e的F、G值
    3. 将节点n存入 close list中
      在这里插入图片描述

  5. 程序运行结束条件（二者满足其一）

    1. 终点在close list中
    2. 无法找到重点，且open list为空

  6. 得到最优路径：从终点开始，每个节点沿着父节点移动，直达到达起点
    在这里插入图片描述

流程图

在这里插入图片描述

代码

A-star.h

#pragma once
#include<vector>
#include<list>using namespace std;const int kCost1 = 10; // 横向、纵向移动代价
const int kCost2 = 14; // 对角线移动代价struct Point
{int x, y; // 点坐标，x为横，y为纵坐标int F, G, H; // F = G + HPoint* parent; // 父代坐标Point(int _x, int _y) : x(_x), y(_y), F(0), G(0), H(0), parent(nullptr) {} // 初始
};class Astar
{
public:void InitAstar(vector<vector<int>>& _maze);list<Point*> GetPath(Point &starPoint, Point &endPoint, bool isIgnoreCorner);
private:Point* findPath(Point &startPoint, Point &endPoint, bool isIgnoreCorner);vector<Point*> getSurrentPoints(const Point* point, bool isIgnoreCorner) const;bool isCanreach(const Point *point, const Point *target, bool isIgnoreCorner) const;  // 判断某点是否可以用于下一步判断Point *isInList(const list<Point *> &list, const Point *point) const; // 判断open_list/close_list中是否包含某点Point* getLeastFpoint(); // 从open_list中返回F值最小的节点// 计算 F G Hint calG(Point *temp_start, Point *point);int calH(Point *point, Point *end);int calF(Point *point);vector<vector<int>> maze; // 存放地图的二维数组list<Point*> openList; // open_list 列表list<Point*> closeList; // close_list 列表};

A-star.cpp

#include "A-star.h"void Astar::InitAstar(vector<vector<int>>& _maze)
{maze = _maze;
}list<Point*> Astar::GetPath(Point& starPoint, Point& endPoint, bool isIgnoreCorner)
{Point* res = findPath(starPoint, endPoint, isIgnoreCorner);list<Point*> path;// 返回路径while (res){path.push_back(res);res = res->parent;}// 情况open list和close listopenList.clear();closeList.clear();return path;
}Point* Astar::findPath(Point& startPoint, Point& endPoint, bool isIgnoreCorner)
{openList.push_back(new Point(startPoint.x, startPoint.y)); // open_list中存入七点，并开辟一个新的下一个节点while (!openList.empty()){auto curPoint = getLeastFpoint(); // 找到最小F值的节点openList.remove(curPoint); // 从open list中将当前节点移出closeList.push_back(curPoint); // 将当前节点存入close list中// 1.找到当前节点相邻的可以通过的格子auto surroundPoints = getSurrentPoints(curPoint, isIgnoreCorner);for (auto& target : surroundPoints){// 2. 对某一个格子进行判断， 若其不在open list中，则加入到open list中， 并设其为父节点 计算其 F G H值if (!isInList(openList, target)){target->parent = curPoint;target->G = calG(curPoint, target);target->H = calH(target, &endPoint);target->F = calF(target);openList.push_back(target);}// 3. 若其在open list中，则计算其G值并 与当前节点进行比较，若其G值大，则不进行任何操作， 否则设置它的父节点为当前节点，并更新G F else{int tempG = calG(curPoint, target);if (tempG < target->G){target->parent = curPoint;target->G = tempG;target->F = calF(target);}}Point* resPoint = isInList(openList, &endPoint);if (resPoint)return resPoint;}}return nullptr;
}vector<Point*> Astar::getSurrentPoints(const Point* point, bool isIgnoreCorner) const
{vector<Point*> surroundPoints;for (int x = point->x - 1; x <= point->x + 1; ++x)for (int y = point->y - 1; y <= point->y; ++y)if (isCanreach(point, new Point(x, y), isIgnoreCorner))surroundPoints.push_back(new Point(x, y));return surroundPoints;
}bool Astar::isCanreach(const Point* point, const Point* target, bool isIgnoreCorner) const
{/*if (target->x < 0 || target->x > maze.size() - 1 || target->y < 0 || target->y > maze[0].size() - 1 || maze[target->x][target->y] == 1 || target->x == point->x && target->y == point->y || isInList(closeList, target))return false;*/if (target->x<0 || target->x>maze.size() - 1|| target->y<0 || target->y>maze[0].size() - 1|| maze[target->x][target->y] == 1|| target->x == point->x && target->y == point->y|| isInList(closeList, target)) //如果点与当前节点重合、超出地图、是障碍物、或者在关闭列表中，返回falsereturn false;else{只有对角线才能进行搜索//if (abs(point->x - target->x) + abs(point->y - target->y) == 1)//	return true;//else//{//	// 对角线需要判断是否会遇到障碍//	if (maze[point->x][target->y] == 0 && maze[target->x][point->y] == 0)//		return true;//	else//		return isIgnoreCorner;//}return true;}
}// 判断某个节点是否在列表中
Point* Astar::isInList(const list<Point*>& list, const Point* point) const
{for (auto p : list)if (p->x == point->x && p->y == point->y)return p;return nullptr;
}Point* Astar::getLeastFpoint()
{if (!openList.empty()){auto resPoint = openList.front();for (auto& point : openList){if (point->F < resPoint->F){resPoint = point;}}return resPoint;}return nullptr;
}int Astar::calG(Point* temp_start, Point* point)
{int extraG = (abs(point->x - temp_start->x) + abs(point->y - temp_start->y)) == 1 ? kCost1 : kCost2;int parentG = point->parent == nullptr ? 0 : point->parent->G; // 如果为初始点， 则其父节点为空return parentG + extraG;
}int Astar::calH(Point* point, Point* end)
{// 根据曼哈顿算法进行计算return (abs(point->x - end->x) + abs(point->y - end->y)) * kCost1;//return sqrt((double)(end->x - point->x) * (double)(end->x - point->x) + (double)(end->y - point->y) * (double)(end->y - point->y)) * kCost1;
}int Astar::calF(Point* point)
{return point->G + point->H;
}

main.cpp

#include<iostream>
#include "A-star.h"
#include "A-star2.h"bool InPath(const int &row, const int &col, const list<Point *> &path)
{for (const auto& p : path){if (row == p->x || col == p->y){return true;}}return false;
}int main()
{// 初始化地图，用二维矩阵代表地图，1表示障碍物，0表示可通vector<std::vector<int>> map = { {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},{1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1},{1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1},{1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1},{1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1},{1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1},{1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1},{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1} };Astar astar;astar.InitAstar(map);// 设置起点和目标点Point start(1, 1);Point end(6, 10);// 寻找路径list<Point*> path = astar.GetPath(start, end, false);// 打印路径for (auto& p : path){cout << "(" << p->x << ", " << p->y << ")";}cout << endl;for (int row = 0; row < map.size(); ++row) {for (int col = 0; col < map[0].size(); ++col) {if (InPath(row, col, path)) {if (map[row][col] != 0) {cout << "e ";}else {cout << "* ";}}else {cout << map[row][col] << " ";}}cout << endl;}}

参考链接：
https://www.gamedev.net/reference/articles/article2003.asp
https://blog.csdn.net/A_L_A_N/article/details/81392212
https://zhuanlan.zhihu.com/p/590786438


http://chatgpt.dhexx.cn/article/Q3XtvtIo.shtml

相关文章

python3.6实现的A星算法

python3.6实现的A星算法

A星算法原理: 原理我就不再赘述,可以参考这篇博客https://blog.csdn.net/hitwhylz/article/details/23089415 最近用js写了一遍&#xff0c;用的同样的算法&#xff0c;需要js代码的看这里&#xff1a;https://blog.csdn.net/qq_39687901/article/details/85697127 代码实现: …
阅读更多...
A星寻路算法介绍

A星寻路算法介绍

你是否在做一款游戏的时候想创造一些怪兽或者游戏主角&#xff0c;让它们移动到特定的位置&#xff0c;避开墙壁和障碍物呢&#xff1f; 如果是的话&#xff0c;请看这篇教程&#xff0c;我们会展示如何使用A星寻路算法来实现它&#xff01; 在网上已经有很多篇关于A星寻路算…
阅读更多...
对A星算法的理解

对A星算法的理解

1、A*算法的**搜索区域 ** 传统A星算法是将地图简化成栅格&#xff0c;计算路径时是用每个栅格的中心点作为单位进行计算。 搜索区域分为两部分&#xff1a;开放列表和封闭列表 开放列表可以进行访问&#xff0c;封闭列表则不可以访问&#xff08;包括不可走 (unwalkable) 的方…
阅读更多...
A星算法（Java实现）

A星算法（Java实现）

一、适用场景 在一张地图中&#xff0c;绘制从起点移动到终点的最优路径&#xff0c;地图中会有障碍物&#xff0c;必须绕开障碍物。 二、算法思路 1. 回溯法得到路径 (如果有路径)采用“结点与结点的父节点”的关系从最终结点回溯到起点&#xff0c;得到路径。 2. 路径代…
阅读更多...
A-Star（A*）算法

A-Star（A*）算法

【由于专栏后几篇限制vip观看&#xff0c;我又把完整算法在公众号“武汉AI算法研习”进行了发布&#xff0c;可以查看全专栏文章。】 A-Star(A*)算法作为Dijkstra算法的扩展&#xff0c;在寻路和图的遍历过程中具有一定的高效性。 【适用范围】静态图搜索 【算法流程】A-Sta…
阅读更多...
A星算法代码

A星算法代码

A星算法代码python3实现 前言一、A*&#xff1f; A星1.一个搜索算法2.结果展示 二、使用环境1.python 3.x2.一些解释说明 一些话 前言 产生本文的缘由 学校计科课程要求的小作业, 在csdn上看了好多, 记录一下自己的学习 以下是本篇文章正文内容 一、A*&#xff1f; A星 1.一…
阅读更多...
A星算法(基于matlab)

A星算法(基于matlab)

概述 基于上一篇文章提到的DFS算法和BFS算法 A星算法属于图这种数据结构的搜索算法&#xff0c;对比于树的遍历搜索&#xff0c;需要考虑到的问题是&#xff1a;同一个节点的重复访问&#xff0c;所以需要对于已经访问过的节点进行标记。 曼哈顿距离&#xff1a; 在几何度量空…
阅读更多...
【A星算法】--第四篇（A星算法）

【A星算法】--第四篇（A星算法）

本篇主要介绍A星算法的过程&#xff1a; * 把起始节点加进openList * while openList 不为空 { * 当前节点 openList 中成本最低的节点 * if&#xff08;当前节点 目标节点&#xff09;{ * 路径完成 …
阅读更多...
A星算法详解(个人认为最详细,最通俗易懂的一个版本)

A星算法详解(个人认为最详细,最通俗易懂的一个版本)

A* 寻路算法 原文地址&#xff1a; http://www.gamedev.net/reference/articles/article2003.asp 概述 虽然掌握了 A* 算法的人认为它容易&#xff0c;但是对于初学者来说&#xff0c; A* 算法还是很复杂的。 搜索区域(The Search Area) 我们假设某人要从 A 点移动到 B 点&…
阅读更多...
A星算法理解

A星算法理解

A星算法理解 1.选择A星算法的原因 为了进行路径规划算法是不可回避的&#xff1a;启发式搜索算法是比较常规的一类算法就是在状态空间中的搜索对每一个搜索的位置进行评估&#xff0c;得到最好的位置&#xff0c;再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路…
阅读更多...
A星(A*, A Star)算法详解

A星(A*, A Star)算法详解

MulinB按&#xff1a;经典的智能寻路算法&#xff0c;一个老外写的很透彻很清晰&#xff0c;很容易让人理解神秘的A*算法。以下是一个中文翻译版。 A*寻路初探 GameDev.net 作者&#xff1a; Patrick Lester 译者&#xff1a;Panic 2005年3月18日 译者序&#xff1a;很久以前就…
阅读更多...
A星算法

A星算法

A星算法 1.简述 A星算法就是试图在地图中找到一条最短路径&#xff0c;但不保证一定存在。 任务 小猫去找青蛙玩&#xff08;好TM弱智啊~&#xff09;条件 黑色方块无法通行&#xff0c;每走一个格子小猫消耗的体力都为1。 2.如果说你是小猫&#xff0c;你会怎么走&#xf…
阅读更多...
A星算法说明

A星算法说明

A*算法说明 文章目录 前言原理说明如何构造 h ( n ) h(n) h(n)一、欧氏距离二、曼哈顿距离三、其他 关于 g ( n ) g(n) g(n)路况设置如何实现 完整的流程搜索过程图示允许斜走&#xff0c;使用优先队列禁止斜走&#xff0c;使用优先队列允许斜走&#xff0c;使用普通队列禁止斜…
阅读更多...
A星算法优化（一）启发函数

A星算法优化（一）启发函数

基于Python语言对A星算法进行优化&#xff1a;(视频中会拿python与matlab作对比) 源码地址&#xff1a;https://github.com/Grizi-ju/ros_program/blob/main/path_planning/Astar.py B站详解视频&#xff1a;https://www.bilibili.com/video/BV1FL4y1M7PM?spm_id_from333.999…
阅读更多...
猴子都能看懂的A星算法原理

猴子都能看懂的A星算法原理

文章目录 A星算法基本原理什么是寻路算法算法的思路 算法实现脚本1————cconst.cs脚本2————AStar.cs Unity演示演示样例一演示样例二演示样例三演示样例四 俗话说&#xff0c;好记性不如烂笔头&#xff0c;对于有了解过寻路算法的同学&#xff0c;对于A星算法应该不陌生…
阅读更多...
A星寻路算法详解（C++实现 完整代码+图片演示 ）

A星寻路算法详解（C++实现 完整代码+图片演示 ）

文章目录 三种寻路算法 A星寻路算法A星寻路算法思想A星寻路准备A星寻路过程&#xff08;图例&#xff09;A星寻路代码&#xff08;完整&#xff09; 三种寻路算法 深度寻路算法&#xff1a;不一定能找到最佳路径&#xff0c;但是寻路快速&#xff0c;只能走直线。广度寻路算法…
阅读更多...
A星(A*、A Star)路径规划算法详解（附MATLAB代码）

A星(A*、A Star)路径规划算法详解（附MATLAB代码）

首先看看运行效果&#xff0c;分别有三种模式&#xff0c;代码运行前需要通过鼠标点击设置起点和终点。 第一种模式直接输出最短路径 第二种模式输出最短路径的生成过程 第三种模式输出最短路径的生成过程和详细探索的过程 代码获取 gitee链接&#xff1a;https://gitee.c…
阅读更多...
什么是脏读？不可重复读？幻读？如何解决？

什么是脏读？不可重复读？幻读？如何解决？

什么是脏读&#xff1f;不可重复读&#xff1f;幻读&#xff1f;如何解决&#xff1f; 朋友最近面试美团&#xff0c;被面试官问到数据库的幻读问题&#xff0c;自己正好最近复习到这&#xff0c;做个笔记整理一下数据库的三大特征以及隔离级别。 一.先来回顾一下什么是事务&…
阅读更多...
MySQL理论：脏读、不可重复读、幻读

MySQL理论：脏读、不可重复读、幻读

&#x1f3c6;今日学习目标&#xff1a; &#x1f340;MySQL理论&#xff1a;脏读、不可重复读、幻读 ✅创作者&#xff1a;林在闪闪发光 ⏰预计时间&#xff1a;30分钟 &#x1f389;个人主页&#xff1a;林在闪闪发光的个人主页 &#x1f341;林在闪闪发光的个人社区&#xf…
阅读更多...
数据库事务隔离级别（脏读、幻读、不可重复读）

数据库事务隔离级别（脏读、幻读、不可重复读）

一、脏读、幻读和不可重复读 一、脏读、不可重复读、幻读 1、脏读&#xff1a;脏读就是指当一个事务正在访问数据&#xff0c;并且对数据进行了修改&#xff0c;而这种修改还没有提交到数据库中&#xff0c;这时&#xff0c;另外一个事务也访问这个数据&#xff0c;然后使用了…
阅读更多...
推荐文章

Copyright @ 2022~2023