文章目录
- 灰色关联分析法简介
- 步骤
- 画统计图,进行简单分析
- 确定分析数列
- 对变量进行预处理
- 计算子序列中各个指标与对应母指标的关联系数
- 计算灰色关联度
- 得到结论
- 讨论
- 评价类问题完整分析步骤(该方法)
- 对指标进行正向化
- 预处理
- 得到母序列
- 计算灰色关联度
- 计算各个指标的权重
- 计算得分
- 得分归一化
灰色关联分析法简介
-
灰色关联分析是一种系统分析

-
灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间的关联度就越大,反之就越小。
-
比较少用
步骤
例:下表某地区国内生产总值的统计数据(以百万元计),问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大
| 年份 | 国内生产总值 | 第一产业 | 第二产业 | 第三产业 |
|---|---|---|---|---|
| 2000 | 1988 | 386 | 839 | 763 |
| 2001 | 2061 | 408 | 846 | 808 |
| 2002 | 2335 | 422 | 960 | 953 |
| 2003 | 2750 | 482 | 1258 | 1010 |
| 2004 | 3356 | 511 | 1577 | 1268 |
| 2005 | 3806 | 561 | 1893 | 1352 |
画统计图,进行简单分析

- 四个季度都呈上升趋势
- 第二产业增幅较为明显
- 第二产业与第三产业的差距慢慢变小后又逐渐增大
- ……
确定分析数列
- 母序列(又称参考序列,母指标):能反应系统行为特征的数据序列(类似于因变量Y,此处记为 X 0 X_0 X0)
- 子序列(又称比较序列,子指标):影响系统行为的因素组成的数据序列(类似于自变量X,此处记为 ( x 1 , x 2 , … , x n ) (x_1,x_2,…,x_n) (x1,x2,…,xn))
- 在本例中国内生产总值就是母序列,第一、第二、第三产业就是子序列
对变量进行预处理
- 目的:去量纲、缩小变量范围从而简化计算
- 做法:先求出每个指标的均值,再用该指标中的每个元素除以该均值
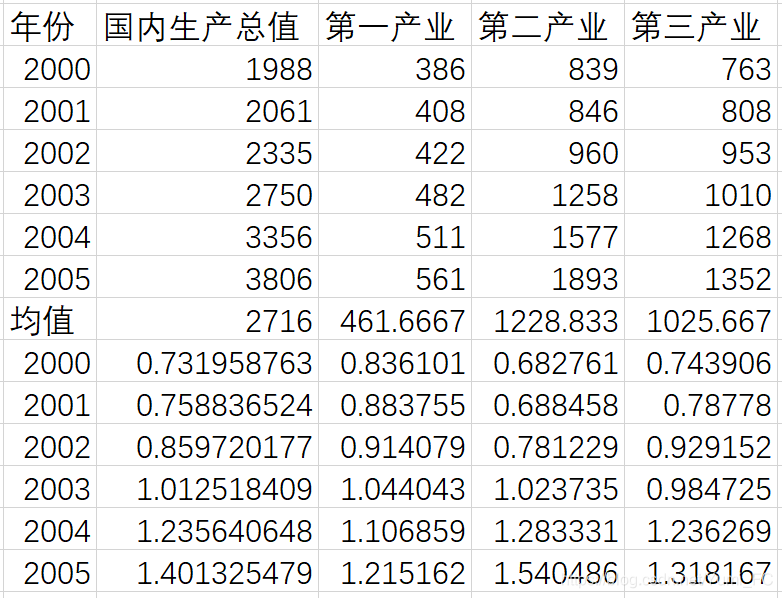
计算子序列中各个指标与对应母指标的关联系数
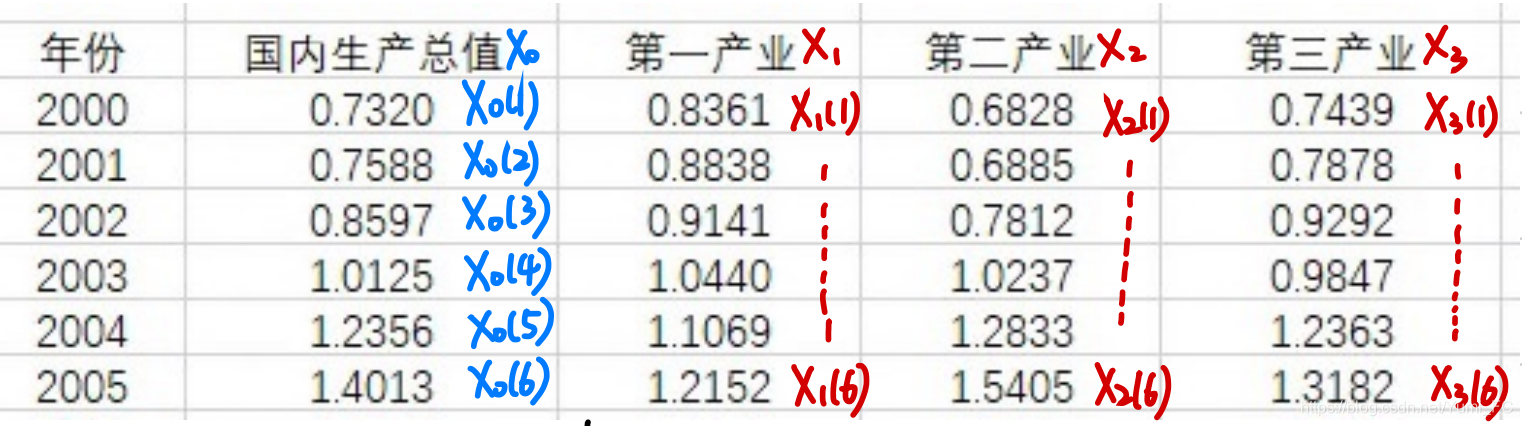
母序列: X 0 = ( X 0 ( 1 ) , X 0 ( 2 ) , … X 0 ( n ) ) ) T X_0=(X_0(1),X_0(2),…X_0(n)))^T X0=(X0(1),X0(2),…X0(n)))T
子序列: { X 1 = ( x 1 ( 1 ) , x 1 ( 2 ) , … x 1 ( n ) ) T X 2 = ( x 2 ( 1 ) , x 2 ( 2 ) , … , x 2 ( n ) ) T … … X m = ( x m ( 1 ) , x m ( 2 ) , … , x m ( n ) ) T \begin{cases}{X_1=(x_1(1),x_1(2),…x_1(n))^T}\\{X_2=(x_2(1),x_2(2),…,x_2(n))^T}\\……\\X_m=(x_m(1),x_m(2),…,x_m(n))^T \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧X1=(x1(1),x1(2),…x1(n))TX2=(x2(1),x2(2),…,x2(n))T……Xm=(xm(1),xm(2),…,xm(n))T
计算:
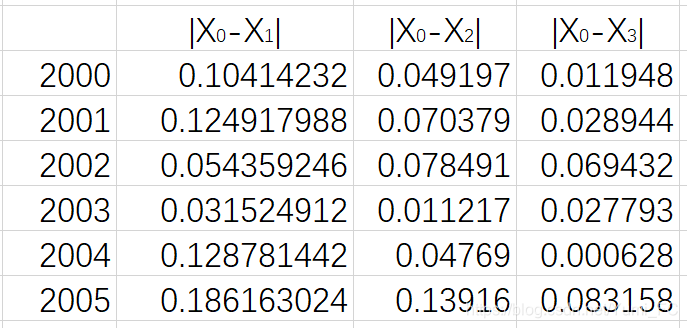
记 a = m i n i m i n k ∣ X 0 ( k ) − x i ( k ) ∣ a=min_imin_k|X_0(k)-x_i(k)| a=minimink∣X0(k)−xi(k)∣为两极最小差,记 b = m a x i m a x k ∣ X 0 ( k ) − x i ( k ) ∣ b=max_imax_k|X_0(k)-x_i(k)| b=maximaxk∣X0(k)−xi(k)∣为两极最大差
则上表中 a = 0.0628 , b = 0.186163024 a=0.0628,b=0.186163024 a=0.0628,b=0.186163024
定义 γ ( x 0 ( k ) , x i ( k ) ) = a + ρ b ∣ x 0 ( k ) − x i ( k ) ∣ + ρ b , ρ \gamma(x_0(k),x_i(k))=\Large \frac {a+\rho b}{|x_0(k)-x_i(k)|+\rho b},\rho γ(x0(k),xi(k))=∣x0(k)−xi(k)∣+ρba+ρb,ρ一般取0.5
结果:
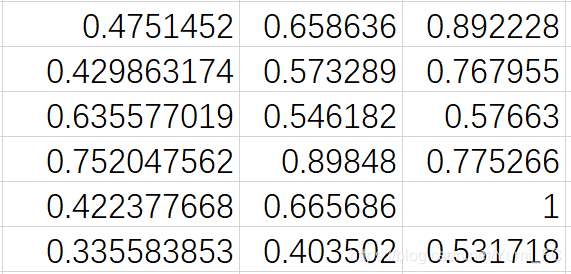
例如: γ ( x 0 ( 1 ) , x 1 ( 1 ) ) = 0.0628 + 0.5 ∗ 0.18613024 0.10414232 + 0.5 ∗ 0.18613024 \gamma(x_0(1),x_1(1))=\Large \frac {0.0628+0.5*0.18613024}{0.10414232+0.5*0.18613024} γ(x0(1),x1(1))=0.10414232+0.5∗0.186130240.0628+0.5∗0.18613024 = 0.4751452 =0.4751452 =0.4751452
计算灰色关联度
定义 γ ( X 0 , X i ) = 1 n ∑ k = 1 n γ ( X 0 ( k ) , X i ( k ) ) \gamma(X_0,X_i)=\frac 1n\sum_{k=1}^{n}\gamma(X_0(k),X_i(k)) γ(X0,Xi)=n1∑k=1nγ(X0(k),Xi(k))为 X 0 X_0 X0和 X i X_i Xi的灰色关联度
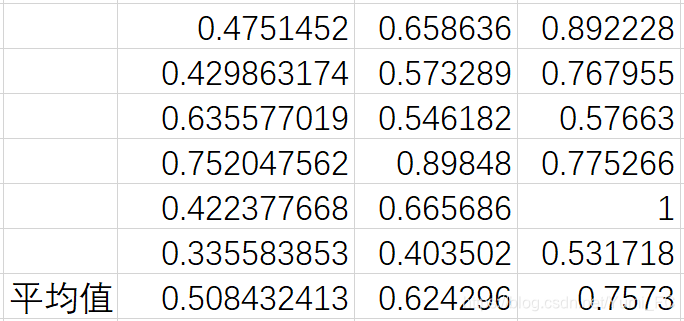
即求平均值
γ ( X 0 , X 1 ) = 0.5084 , γ ( X 0 , X 2 ) = 0.6242 , γ ( X 0 , X 3 ) = 0.7573 \gamma(X_0,X_1)=0.5084,\gamma(X_0,X_2)=0.6242,\gamma(X_0,X_3)=0.7573 γ(X0,X1)=0.5084,γ(X0,X2)=0.6242,γ(X0,X3)=0.7573
得到结论
通过比较三个子序列和母序列的灰色关联度可以得到结论:
- 该地区在2000年到2005年间的国内生产总值受到第三产业影响最大。
讨论
1、什么时候用标准化回归,什么时候用灰色关联分析?
- 当样本个数n较大时,一般使用标准化回归;当样本个数n较少时,才使用灰色关联分析
2、如果母序列有多个指标,应该怎么分析
- 例如 Y 1 , Y 2 Y_1,Y_2 Y1,Y2都是母指标,那么我们先计算 Y 1 Y_1 Y1与子序列的灰色关联度,再计算 Y 2 Y_2 Y2与子序列的灰色关联度
评价类问题完整分析步骤(该方法)
对指标进行正向化
预处理
- 如前面的步骤进行预处理(先求出每个指标的均值,再用该指标中的每个元素除以该均值)
- 得到矩阵 Z n x m = ( Z i j ) n x m Z_{nxm}=(Z_{ij})_{nxm} Znxm=(Zij)nxm
得到母序列
(若无实质母序列)将预处理后的矩阵的每一行取出最大值构成母序列(虚构的)
计算灰色关联度
得到 γ 1 , γ 2 , … , γ m \gamma_1,\gamma_2,…,\gamma_m γ1,γ2,…,γm
计算各个指标的权重
ω 1 = γ 1 ( γ 1 + γ 2 + … + γ m ) , ω 2 = γ 2 ( γ 1 + γ 2 + … + γ m ) , … , ω m = = γ m ( γ 1 + γ 2 + … + γ m ) \omega_1=\frac {\gamma_1}{(\gamma_1+\gamma_2+…+\gamma_m)},\omega_2=\frac {\gamma_2}{(\gamma_1+\gamma_2+…+\gamma_m)},…,\omega_m==\frac {\gamma_m}{(\gamma_1+\gamma_2+…+\gamma_m)} ω1=(γ1+γ2+…+γm)γ1,ω2=(γ1+γ2+…+γm)γ2,…,ωm==(γ1+γ2+…+γm)γm
计算得分
第k个评价对象得分: S k = ∑ i = 1 m Z k i ∗ ω i ( k = 1 , 2 , 3 , … , n ) S_k=\sum_{i=1}^mZ_{ki}*\omega_i (k=1,2,3,…,n) Sk=∑i=1mZki∗ωi(k=1,2,3,…,n)
得分归一化
S 1 ′ = S 1 S 1 + S 2 + … + S n , S 2 ′ = S 2 S 1 + S 2 + … + S n , … S n ′ = S n S 1 + S 2 + … + S n S'_1=\frac {S_1}{S_1+S_2+…+S_n},S'_2=\frac {S_2}{S_1+S_2+…+S_n},…S'_n=\frac {S_n}{S_1+S_2+…+S_n} S1′=S1+S2+…+SnS1,S2′=S1+S2+…+SnS2,…Sn′=S1+S2+…+SnSn