灰色关联度分析（Grey Relation Analysis，GRA），是一种多因素统计分析的方法。简单来讲，就是在一个灰色系统中，我们想要了解其中某个我们所关注的某个项目受其他的因素影响的相对强弱，再直白一点，就是说：我们假设以及知道某一个指标可能是与其他的某几个因素相关 的，那么我们想知道这个指标与其他哪个因素相对来说更有关系，而哪个因素相对关系弱一点，依次类推，把这些因素排个序，得到一个分析结果，我们就可以知道我们关注的这个指标，与因素中的哪些更相关。

（ note ： 灰色系统这个概念的提出是相对于白色系统和黑色系统而言的。这个概念最初是由控制科学与工程（hhh熟悉的一级学科）的教授邓聚龙提出的。按照控制论的惯例，颜色一般代表的是对于一个系统我们已知的信息的多少，白色就代表信息充足，比如一个力学系统，元素之间的关系都是能够确定的，这就是一个白色系统；而黑色系统代表我们对于其中的结构并不清楚的系统，通常叫做黑箱或黑盒的就是这类系统。灰色介于两者之间，表示我们只对该系统有部分了解。）

例题：

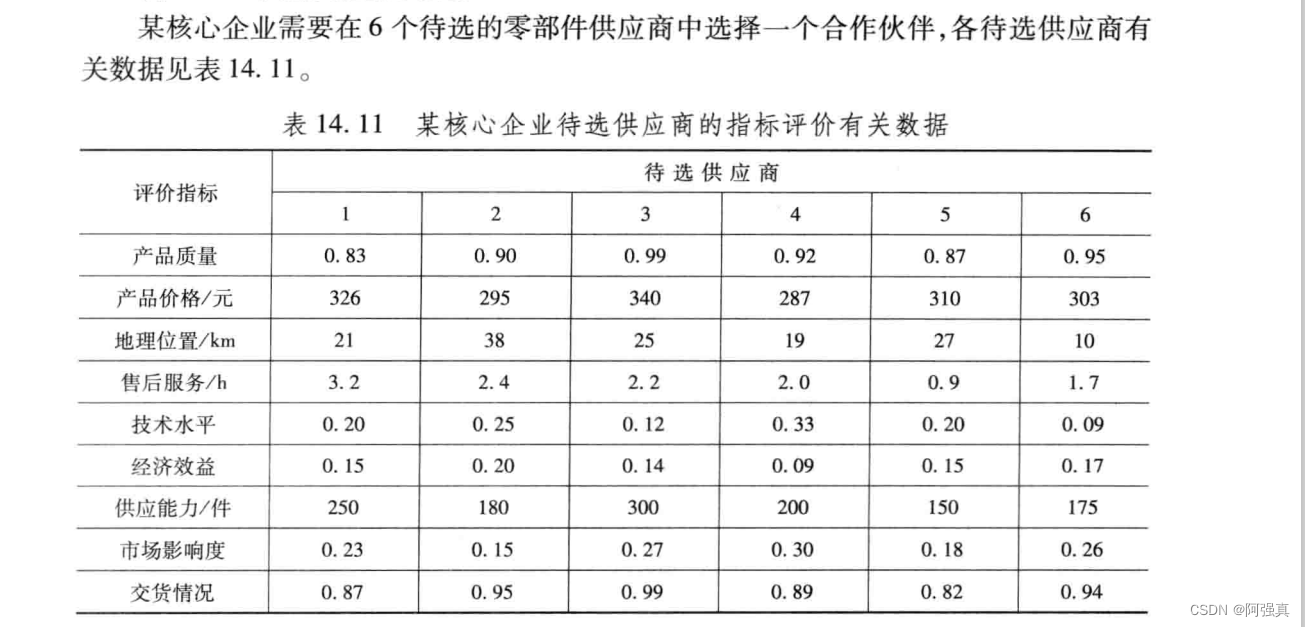
输入数据

输入数据并用DT包的datatable函数展示数据

install.packages("DT")
library(DT)

A <- c(0.83,326,21,3.2,0.2,0.15,250,0.23,0.87)
B <- c(0.90,295,38,2.4,0.25,0.2,180,0.15,0.95)
C <- c(0.99,340,25,2.2,0.12,0.14,300,0.27,0.99)
D <- c(0.92,287,19,2,0.33,0.09,200,0.3,0.89)
E <- c(0.87,310,27,0.9,0.20,0.15,150,0.18,0.82)
F <- c(0.95,303,10,1.7,0.09,0.17,175,0.26,0.94)
data <- data.frame(A,B,C,D,E,F)
rownames(data) <- c("产品质量","产品价格","地理位置","售后服务","技术水平","经济效益","供应能力","市场影响度","交货情况")
library(DT)
datatable(data)

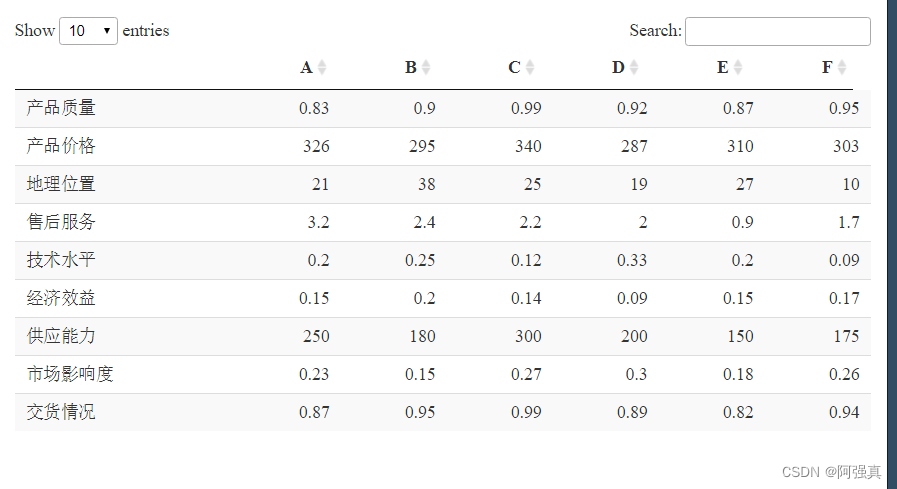
ABDDEF分别对应第1到第6个供应商

数据的标准化/归一化

产品质量、技术水平、供应能力、经济效益、交货情况、市场影响度指标属于效益型指
产品价格、地理位置、售后服务指标属于成本型指标。现分别对上述指标进行规范化：
对于效益型指标（正项指标）标准化公式为：
$$x^{\ast }=\frac{x-min\left(x\right)}{max\left(x\right)-min\left(x\right)}$$
对于成本型指标（逆向指标）标准化公式为：
$$x^{\ast }=\frac{max\left(x\right)-x}{max\left(x\right)-min\left(x\right)}$$
编写函数

#归一化函数正向指标
normalize <- function(x){return ((x-min(x))/(max(x)-min(x)))
}
#归一化函数逆向指标
normalize1 <- function(x){return ((max(x)-x)/(max(x)-min(x)))
}

pos <- apply(data[c(1,5:9),],1,normalize)
neg <- apply(data[c(2:4),],1,normalize1)
scaledata <- cbind(pos,neg);scaledata
scaledata <- t(round(scaledata,3))#这里还求了一个转置
datatable(scaledata)

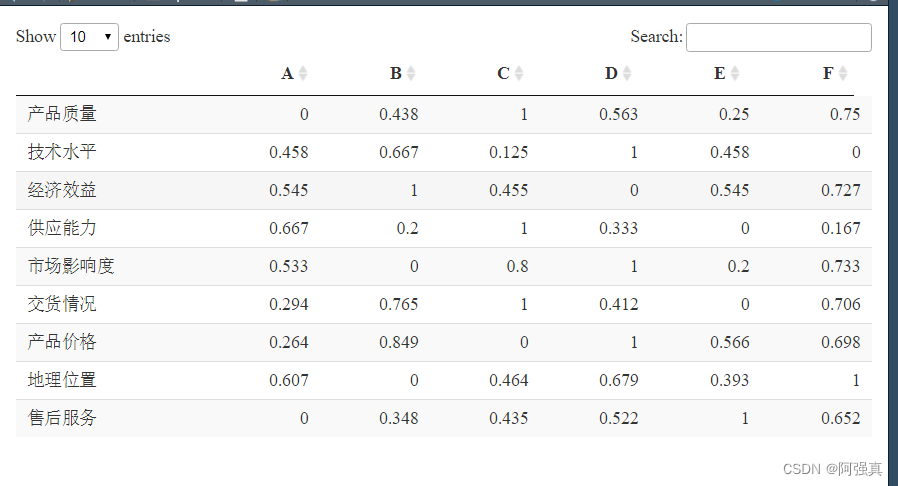
建立参考序列，即每一列的最大值，并合并数据

best <- apply(scaledata,1,max)
data1 <-data.frame(scaledata,best);
datatable(data1,caption="比较数列和参考序列值")

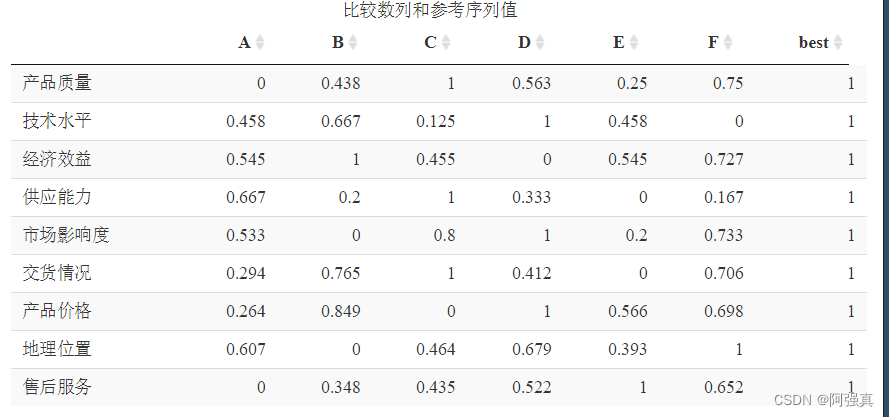
求灰色系数

求差序列和最大值最小值

$${\xi }_i\left(k\right)=\frac{\min \min \left|\left(x_0\left(t\right)-x_s\left(t\right)\right)\right|+\rho \max \max \left|x_0\left(t\right)-x_s\left(t\right)\right|}{\left|x_0\left(t\right)-x_s\left(t\right)\right|+\rho \max \max \left|x_0\left(t\right)-x_s\left(t\right)\right|}$$
这里$x_0(t)$就是标准化后的数据，$x_s(t)就是比较数据，即每一行的最大值首先求出
$$\left|\left(x_0\left(t\right)-x_s\left(t\right)\right)\right|$$

需要主要的是
这里的$\min \min \left|\left(x_0\left(t\right)-x_s\left(t\right)\right)\right|\text{和}\max \max \left|x_0\left(t\right)-x_s\left(t\right)\right|$用R语言的min和max函数就能求（因为matlab的min函数是求每一列的最小值，所所以在matlab中用min（min））
这里的$\rho$一般取0.5

err <-abs((1-scaledata))
datatable(err)
min <- min(err)
max <- max(err)

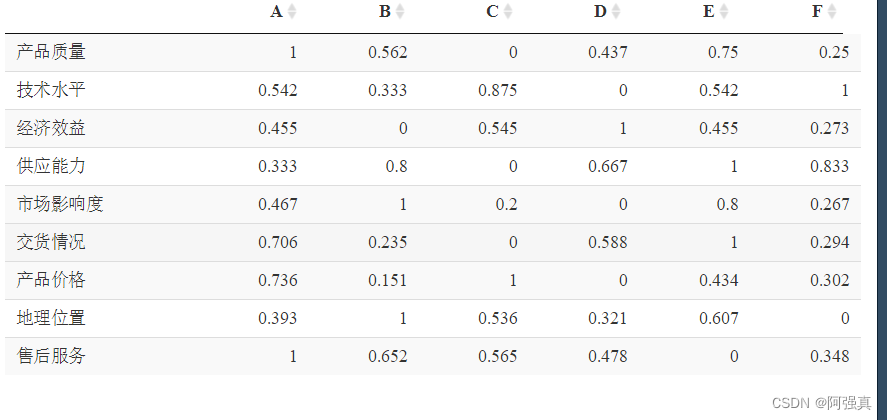
求关联系数

#计算关联系数
rho <-  0.5#分辨系数
xishu <- (min + rho * max)/(err + rho * max)#计算灰色关联分析
xishu <- round(xishu,3)
datatable(xishu)

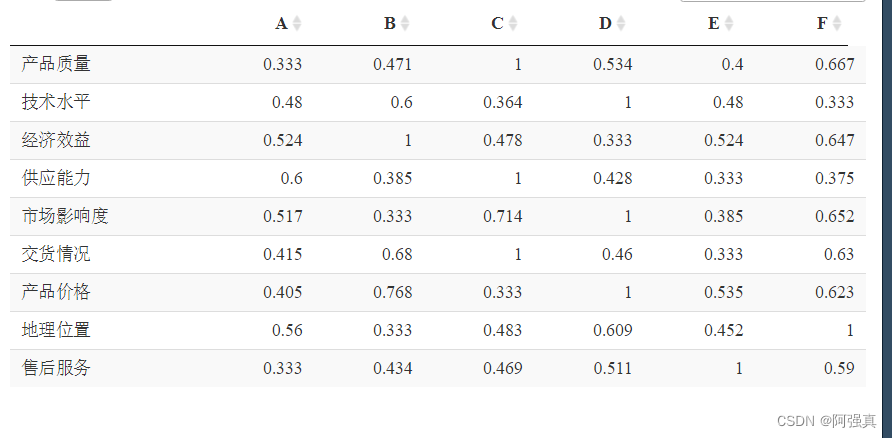
计算关联度并排序

关联度最好求了，只需要对每一类求一个平均值
最后用sort函数排序就行了

#计算关联度
sort(apply(xishu, 2, mean),decreasing = T)

可以看出D的关联度最高，因此应该选择4号供应商（D对应4）

所有代码

创作不易如果对您有帮助，还请点赞

install.packages("DT")
library(DT)
A <- c(0.83,326,21,3.2,0.2,0.15,250,0.23,0.87)
B <- c(0.90,295,38,2.4,0.25,0.2,180,0.15,0.95)
C <- c(0.99,340,25,2.2,0.12,0.14,300,0.27,0.99)
D <- c(0.92,287,19,2,0.33,0.09,200,0.3,0.89)
E <- c(0.87,310,27,0.9,0.20,0.15,150,0.18,0.82)
F <- c(0.95,303,10,1.7,0.09,0.17,175,0.26,0.94)
data <- data.frame(A,B,C,D,E,F)
rownames(data) <- c("产品质量","产品价格","地理位置","售后服务","技术水平","经济效益","供应能力","市场影响度","交货情况")
library(DT)
datatable(data)
#归一化函数正向指标
normalize <- function(x){return ((x-min(x))/(max(x)-min(x)))
}
#归一化函数逆向指标
normalize1 <- function(x){return ((max(x)-x)/(max(x)-min(x)))
}
pos <- apply(data[c(1,5:9),],1,normalize)
neg <- apply(data[c(2:4),],1,normalize1)
scaledata <- cbind(pos,neg);scaledata
scaledata <- t(round(scaledata,3))
datatable(scaledata)
best <- apply(scaledata,1,max)
data1 <-data.frame(scaledata,best);
datatable(data1,caption="比较数列和参考序列值")
#计算差序列
err <-abs((1-scaledata))
datatable(err)
min <- min(err)
max <- max(err)
#计算关联系数
rho <-  0.5#分辨系数
xishu <- (min + rho * max)/(err + rho * max)#计算灰色关联分析
xishu <- round(xishu,3)
datatable(xishu)
#计算关联度
sort(apply(xishu, 2, mean),decreasing = T)