熵值法

在信息论中，熵值能够很好的反映信息无序化程度，其值越小，系统无序度越低，信息的效用值越大，其权重也相应越大；反之，其值越大，系统无序度越高，信息的效用值越小，权重也越小。

步骤

熵值法赋权计算步骤如下：
1）确定 $m$ 个需进行评价的样本对象和 $n$ 个评价指标，构建一个对应的判断矩阵 $R=(x_{ij})_{mn},(i=1,2,...,m，j=1,2,...n)$ .
2）将判断矩阵进行标准化，即将各指标进行同度量化。该模型采用比重法对指标判断矩阵原始值进行标准化：
$P_{i j}=\frac{x_{i j}}{\sum_{i=1}^{m} x_{i j}}$
3）计算第 $j$ 项指标的熵值，利用熵值公式计算评价指标的熵值：
$e_{j}=-k \sum_{i=1}^{m} P_{i j} \ln P_{i j}, \text { 其中 } k=\frac{1}{\ln m}(i=1, \ldots, m ; j=1, \ldots, n)$
4）计算第 $j$ 项指标的差异性系数 $g_j$ 。熵值越小，指标间差异性越大，指标在综合评价中所起作用就越大：
$g_j=1-e_j$
5）用熵值法估算各指标的权重，本质上是计算各项指标的价值系数，最后可以得到第 $j$ 项指标的权重系数 $\omega_j$ ：
$\omega_{j}=\frac{g_{j}}{\sum_{i=1}^{n} g_{j}}$

python实现

def Entropy_(standardized_data,weight_num=None,up_layer_num=None,weight_interval=None):''':param standardized_data: 需要计算权重的数据:param weight_num: 权重个数:param up_layer_num: 是否要计算第二层权重，需要则传入上层指标个数:param weight_interval: 若要计算第二层权重，传入第一层指标个数区间:return: 第一层的差异性系数g，权重w,熵值e'''rows, cols = standardized_data.shapek = 1/math.log(rows)standardized_data_arr = np.array(standardized_data)standardized_data_log = np.log(standardized_data_arr)use_data = pd.DataFrame(standardized_data_arr*standardized_data_log)use_data.loc['col_sum'] = use_data.apply(lambda x:x.sum())#计算熵值e = use_data.loc['col_sum']*(-k)#计算差异性系数g = 1-eif up_layer_num is not None:#权重计算g_arr = np.zeros(shape=[up_layer_num])for i in range(up_layer_num):for j in weight_interval[i]:g_arr[i] = g_arr[i] + g.iloc[j]#权重w = np.zeros(weight_num)for i in range(up_layer_num):for j in weight_interval[i]:w[j] = g[j] / g_arr[i]else:# 权重计算w = np.array([i/np.sum(g) for i  in g])w = pd.DataFrame(w)return g,e,w

灰色关联分析

灰色系统理论的研究对象是部分信息已知而部分信息未知的“贫信息”’不确定性系统，利用已知信息来确定系统的未知信息，对样本量没有严格的规定，也不要求服从任何典型分布规律，且不会出现量化结果与定性分析不一致的情况。而关联分析是灰色系统分析、评级和决策的基础，其基本思想是根据数据指标呈现出的序列曲线的几何形状相似程度来判断两个指标之间的联系是否紧密，通过关联度表征两个事物间的关联程度。

灰色关联度分析步骤

1）延用熵值法中构建的原始数据判断矩阵 $R=(x_{ij})_{m×n}$ ,矩阵如下：
$R=\left[\begin{array}{ccc} x_{11} & \cdots & x_{1 n} \\ \vdots & \ddots & \vdots \\ x_{m 1} & \cdots & x_{m n} \end{array}\right]$
2）选取最优指标集
各评价指标的最优值组成的集合称为最优集，它是评价对象比较的基准，记录为
$F=k_j,(j=1,2,3,...,n)$
式子中 $k_j$ 为第 $j$ 个指标的最优值。在最优值的选取过程中，若指标为成本型指标，则最优值选取当中的最小值；若指标为效益型指标，则最优值选取当中的最大值。最优指标集和各待评价对象的指标组成一个矩阵 D：
$D=\left[\begin{array}{ccc} k_{1} & \cdots & k_{n} \\ x_{1} & \cdots & x_{n} \\ \vdots & \ddots & \vdots \\ x_{m 1} & \cdots & x_{m n} \end{array}\right]$
式中， $x_{ij}$ 为第 $i$ 个评价对象的第 $j$ 个指标的原始数值.
3）计算关联系数，求取评判矩阵
根据灰色系统理论，将最优数列作为参考数列，将其他数列作为被比较数列，用关联分析法分别求得第 $i$ 个评价对象的第 $j$ 个指标与第 $j$ 个最优指标的关联系数 $e_{ij}$ ，计算公式如下：
$e_{i j}=\frac{\min _{i} \min _{j}\left|k_{j}-x_{i j}\right|+\rho \max _{i} \max _{j}\left|k_{j}-x_{i j}\right|}{\left|k_{j}-x_{i j}\right|+\rho \max _{i} \max _{j}\left|k_{j}-x_{i j}\right|}$
式中， $\rho$ 为分辨系数，其取值范围在[0,1]，一般取 $\rho=0.5$ ； $\min _{i} \min _{j}\left|k_{j}-x_{i j}\right|$ 为两级最小差， $\max _{i} \max _{j}\left|k_{j}-x_{i j}\right|$ 为两级最大差。
则各指标的评判矩阵即关联系数记录为 $E$ ，如下：
$E=\left[\begin{array}{ccc} e_{11} & \cdots & e_{1 n} \\ \vdots & \ddots & \vdots \\ e_{m 1} & \cdots & e_{m n} \end{array}\right]$
式中， $e_{ij}$ 为第 $i$ 个样本第 $j$ 个指标与第 $j$ 个最优指标的关联系数。
4）建立灰色单层次评判矩阵
$R X = E \times W$
式中， $X=\left[r_{1}, r_{2}, \ldots, r_{m}\right]^{T}$ 为 $m$ 个被评价对象的综合评价结果向量；即 $r_i = \sum_{i=1}^{m} \omega_{j}e_{ij}$ ； $W=\left[\omega_1,\ldots,\omega_n \right]$ 为 $n$ 个评价指标的权重分配向量，其中 $\sum_{j=1}^{n} \omega_{j}=1$ 。
5）根据实际指标情况，可建立多层评判标准
当评价对象的各个指标间分为不同层次时，需要采用多层次综合评价法。灰色多层次综合评判是以单层次综合评价为基础，需将单层次评价结果矩阵作为下一个层次的原始指标列，再重复进行下一层次单层评判计算，依次类推至最高层。若灰色关联度越大，说明该评价对象与参考指标越接近，即第 $i$ 个评价对象越优于其他，通过关联度这指标排出样本之间的优劣次序。

python实现

暂无

层次分析法

层次分析法，简称AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。
层次分析法属于主观赋权法，具有简洁、系统性分析的优点，但主观性强，不易令人信服，并且当数据量较大时，权重难以确定。

计算步骤

1）建立层次结构模型
将决策的目标、考虑的因素（决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。最高层是指决策的目的、要解决的问题。最低层是指决策时的备选方案。中间层是指考虑的因素、决策的准则。对于相邻的两层，称高层为目标层，低层为因素层。
2）构造判断(成对比较)矩阵
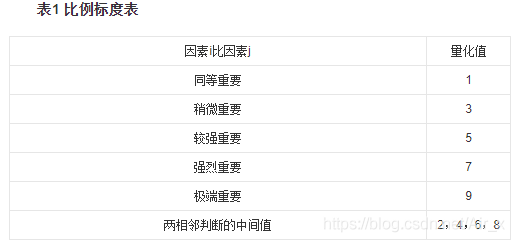
两两因素相互比较，对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。如对某一准则，对其下的各方案进行两两对比，并按其重要性程度评定等级。为要素与要素重要性比较结果，表1列出Saaty给出的9个重要性等级及其赋值。按两两比较结果构成的矩阵称作判断矩阵：
重要性等级及赋值
3）层次单排序及其一致性检验
对应于判断矩阵最大特征根 $\lambda_{max}$ 的特征向量，经归一化后记为 $W$ 。 $W$ 的元素为同一层次因素对于上一层次因素某因素相对重要性的排序权值，这一过程称为层次单排序。能否确认层次单排序，则需要进行一致性检验，所谓一致性检验是指对 $A$ 确定不一致的允许范围。其中， $n$ 阶一致阵的唯一非零特征根为 $n$ ；$n $阶正互反阵$ A$的最大特征根 $\lambda ≥n$ ，当且仅当 $\lambda = n$ 时， $A$ 为一致矩阵。
一致性指标用CI计算，CI越小，说明一致性越大，计算公式为：
$\frac{\lambda-n}{n-1}$
$C I = 0$ ，有完全的一致性； $C I$ 接近于 $0$ ，有满意的一致性； $C I$ 越大，不一致越严重。
为衡量 $C I$ 的大小，引入随机一致性指标 $R I$ ：
$RI=\frac{CI_1+CI_2+\dots+CI_n}{n}$
其与矩阵阶数的关系，一般情况下，矩阵阶数越大，则出现一致性随机偏离的可能性也越大，其对应关系如表2：
在这里插入图片描述
考虑到一致性的偏离可能是由于随机原因造成的，因此在检验判断矩阵是否具有满意的一致性时，还需将 $C I$ 和随机一致性指标 $R I$ 进行比较，得出检验系数 $C R$ ，公式如下：
$CR=\frac{CI}{RI}$
一般，如果 $C R < 0.1$ ，则认为该判断矩阵通过一致性检验，否则就不具有满意一致性。
4）层次总排序及其一致性检验

python实现

# python3.7
# -*- coding: utf-8 -*-
#@Author    : huinono
#@Software  : PyCharmimport warnings
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as pltwarnings.filterwarnings('ignore')mpl.rcParams['font.sans-serif'] = 'SimHei'
mpl.rcParams['axes.unicode_minus'] = 'False'plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = 'False''''
1、构建判断矩阵：准则层和方案层判断矩阵
2、对方案层判断矩阵求特征向量
3、计算最大特征值与层次单排序的一致性检验
4、层次总排序的一致性检验
5、求得权重
'''
class AHP(object):def __init__(self):self.RI = [0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]def VectorsCal(dself,data):data_sum = np.sum(data,axis=1)data_mean = data_sum/data.shape[0]data_vecs = data_mean/np.sum(data_mean)return data_vecsdef SOConsistencyCheck(self,vals_max,n):CI = (vals_max-n)/(n-1)if CI == 0:CR=0RI = self.RI[n - 1]else:RI = self.RI[n-1]CR = CI/RIreturn CR,CI,RIdef weightCal(self,weight_interval,weight_num,JudgmentMatrix_all):'求特征向量'matrix_vecs_ = [self.VectorsCal(con) for con in JudgmentMatrix_all]'计算最大特征值和单排序一致性检验'matrix_vals_vecs = [np.linalg.eig(con) for con in JudgmentMatrix_all]matrix_vals_max = [np.max(vals_vecs[0]) for vals_vecs in matrix_vals_vecs]matrix_CR = [self.SOConsistencyCheck(matrix_vals_max[i], JudgmentMatrix_all[i].shape[0])[0] for i in range(len(matrix_vals_max))]matrix_CI = [self.SOConsistencyCheck(matrix_vals_max[i], JudgmentMatrix_all[i].shape[0])[1] for i in range(len(matrix_vals_max))]matrix_RI = [self.SOConsistencyCheck(matrix_vals_max[i], JudgmentMatrix_all[i].shape[0])[2] for i in range(len(matrix_vals_max))]'总排序一致性检验'C1 = matrix_vecs_[-1].reshape(-1, 1)matrix_zero = np.zeros(weight_num)P = []length = len(weight_interval)for i in range(length):if i == 0:P1 = np.concatenate([matrix_vecs_[i], matrix_zero[weight_interval[i][-1] + 1:]], axis=0).reshape(-1, 1)P.append(P1)elif i == length-1:P3 = np.concatenate([matrix_zero[:weight_interval[i][0]], matrix_vecs_[i]], axis=0).reshape(-1, 1)P.append(P3)else:P2 = np.concatenate([matrix_zero[:weight_interval[i][0]], matrix_vecs_[i], matrix_zero[weight_interval[i][-1] + 1:]],axis=0).reshape(-1, 1)P.append(P2)weight_one = np.dot(np.concatenate(P, axis=1), C1)if np.dot(matrix_CI[1:], C1) == 0 and np.dot(matrix_RI[1:],C1) == 0:CR1 = 0else:CR1 = np.dot(matrix_CI[1:], C1) / np.dot(matrix_RI[1:],C1)return weight_one,matrix_CR,CR1,matrix_vecs_,matrix_vals_max