欧拉回路
- 几个定义
- 性质与定理
  - 定理1
    - 推论1
  - 定理2
    - 推论2
  - 性质1
  - 性质2
算法主体
例题
- uoj117求给定图的欧拉回路
- poj1041求字典序最小的欧拉回路
- poj1386Play on Words
- poj2230求无向图欧拉图要求每条边走两遍且方向不同
- poj2513字符串的欧拉图
- poj2337字典序
- poj1637Sightseeing tour求混合图欧拉回路
- HDU 2894Poj1392

欧拉回路

几个定义

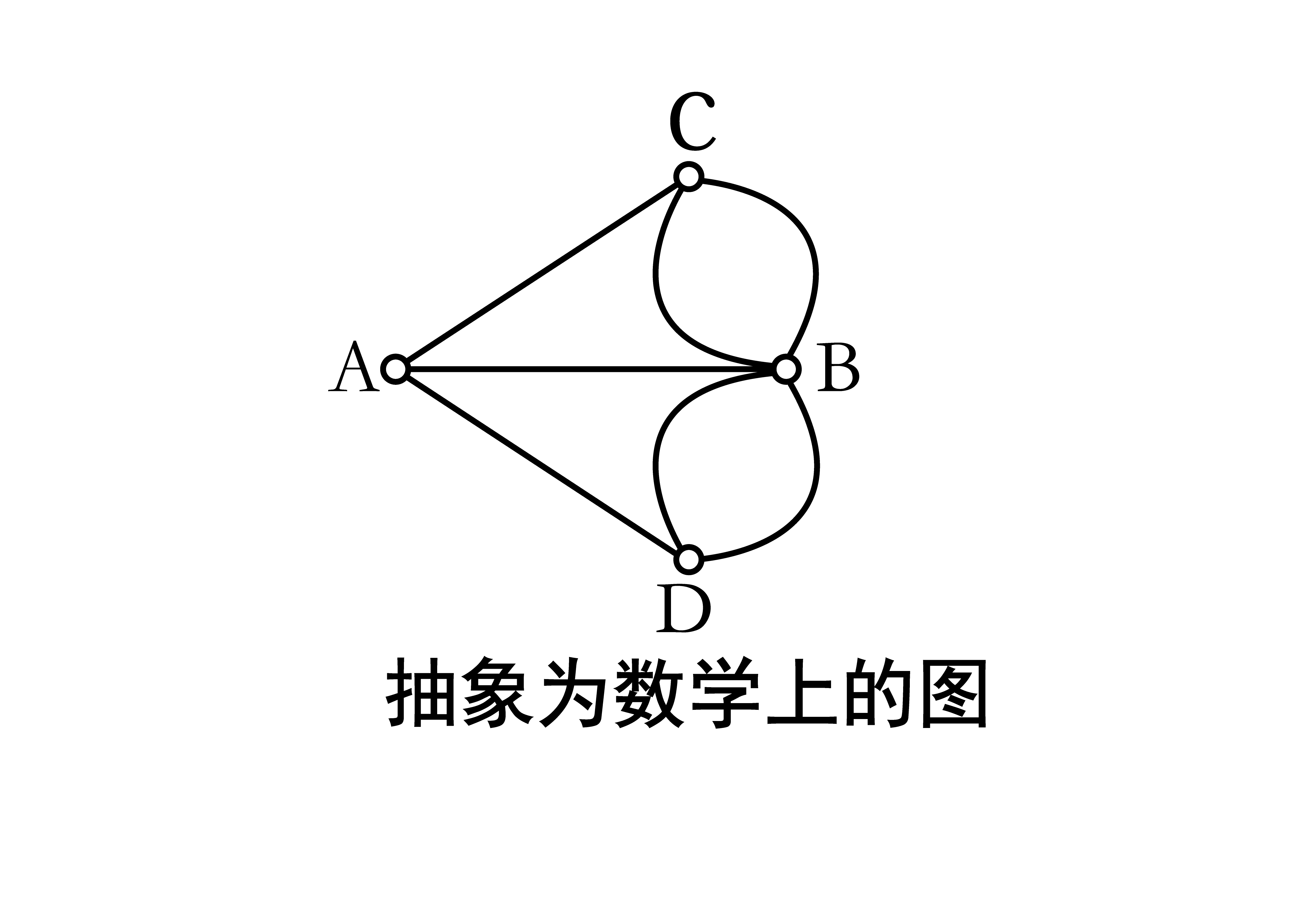
设G (V,E)是一个图。
1.欧拉回路图G中经过每条边一次并且仅一次的回路称作欧拉回路。
2.欧拉路径图G中经过每条边一次并且仅一次的路径称作欧拉路径。
3.欧拉图存在欧拉回路的图称为欧拉图。
4.半欧拉图存在欧拉路径但不存在欧拉回路的图称为半欧拉图。

性质与定理

二、性质与定理

在以下讨论中，假设图 G不存在孤立点（度为0）；否则，先将所有孤立点从图中删除。显然，这样做并不会影响图G中欧拉回路的存在性。

我们经常需要判定一个图是否为欧拉图（或半欧拉图），并且找出一条欧拉回路（或欧拉路径）。对于无向图有如下结论：

定理1

无向图G为欧拉图，当且仅当G为连通图且所有顶点的度为偶数。

证明：
必要性。
设图G的一条欧拉回路为C。由于C经过图G的每一条边，而图G没有孤立点，所以C也经过图G的每一个顶点，G为连通图成立。而对于图G的任意一个顶点 v，经过C时都是从一条边进入，从另一条边离开，因此v经过C的关联边的次数为偶数。又由于C不重复地经过了图G的每一条边，因此的度为偶数。

充分性
假设图G中不存在回路，而G是连通图，故一定是G树，那么有 $|E|=|V|-1$ 由于图G所有顶点的度为偶数而且不含孤立点，那么图G的每一个顶点的度至少为2。由握手定理，有 $|E|=\frac{1}{2}\sum\limits_{v\in V}d(v)\ge V$ ，与假设相矛盾。故图G中一定存在回路。设图G中边数最多的一条简单回路边没有重复出现为 $C=\{e_1=(v_0,v_1),e_2=(v1,v2),...,e_m=(v_{m-1},v_0)\}$
下面证明回路C是图G的欧拉回路
假设C不是欧拉回路,则C中至少含有一个点 $v_k$ ,该点的度大于C经过该点的关联边的次数。令 $v_0^{'}=v_k$ ，从 $v_0^{'}$ 出发有一条不属于C的边 $e_1^{'}=(v_0^{'},v_1^{'})$ 。若 $v_0^{'}=v_1^{'}$ ,则 $v_0^{'}$ 自身成环，可以将其加入C中形成一个更大的回路。否则若 $v_0^{'}\not =v_1^{'}$ ,由于 $v_1^{'}$ 的度为偶数,而C中经过 $v_1^{'}$ 的关联边的次数也是偶数,所以必然存在一条不属于C的边 $e_2^{'}=(v_1^{'},v_2^{'})$ 依此类推，存在不属于C的边 $e_3^{'}=(v_2^{'},v_3^{'}),...,e_k^{'}=(v_{k-1}^{'},v_0^{'})$ .
故 $C^{'}=\{e_1^{'},e_2^{'},...,e_k^{'}\}$ 是一条新的回路，将其加入C中可以形成一个更大的回路。这与C是图G的最大回路相矛盾，故C是图G的欧拉回路。

推论1

无向图G为半欧拉图，当且仅当G为连通图且除了两个顶点的度为奇数之外，其它所有顶点的度为偶数。

证明：将两个度为奇数的顶点连接，由定理一得该图为欧拉图，故去掉环上一边为半欧拉图。

定理2

有向图G为欧拉图，当且仅当G的基图连通，且所有顶点的入度等于出度。

推论2

有向图G为半欧拉图，当且仅当G的基图连通，且存在顶点u的入度比出度大1 、v的入度比出度小 1，其它所有顶点的入度等于出度。

证明同定理1相似。

性质1

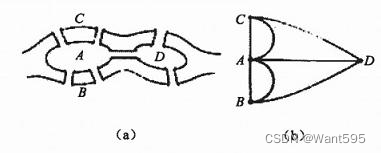
设C是欧拉图G中的一个简单回路，将C中的边从图G中删去得到一个新的图G $^{'}$ ,则 G $^{'}$ 的每一个极大连通子图都有一条欧拉回路。

证明
若G为无向图，则图G $^{'}$ 的各顶点的度为偶数；若G为有向图，则图 G $^{'}$ 的各顶点的入度等于出度。

性质2

设 C1、C2是图G的两个没有公共边，但有至少一个公共顶点的简单回路，我们可以将它们合并成一个新的简单回路。
这里写图片描述

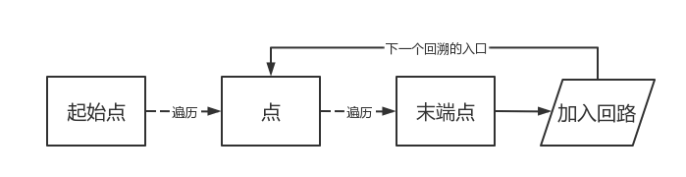
算法主体

由此可以推出欧拉图的算法：

1 在图G中任意找一个回路C；
2 将图G中属于回路C的边删除；
3 在残留图的各极大连通子图中分别寻找欧拉回路；
4 将各极大连通子图的欧拉回路合并到C中得到图G的欧拉回路。

例题

uoj117：求给定图的欧拉回路

描述很简单，但有许多坑点。
1.孤立点要舍弃。
2.对于孤立点成子环的欧拉回路不合法。（这个好做，dfs判断边条数即可）
3.对于访问过的边不能直接打标记跳过。（如果一直给自环那么dfs循环边就是 $n^2$ ）。

对于第三点可以做如下优化：

for(int &e=last[now];e;e=before[e])

通过改变last来删除边，保证了 $O(E)$ 的时间复杂度。

Code

#include<bits/stdc++.h>
using namespace std;
const int Maxn=2e5+50;
inline int read()
{char ch=getchar();int i=0,f=1;while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}return i*f;
}int maxind,n,m,cnt,ecnt=1,before[Maxn*2],to[Maxn*2],last[Maxn],st[Maxn*2],top,vis[Maxn*2],in[Maxn],out[Maxn];
int st2[Maxn*2],top2;
inline void add(int x,int y)
{ecnt++;before[ecnt]=last[x];last[x]=ecnt;to[ecnt]=y;
}
inline void dfs2(int now)
{for(int &e=last[now];e;e=before[e]){if(vis[e])continue;cnt++;int t=e;vis[e]=1;dfs2(to[e]);st2[++top2]=t;}
}
inline bool check2()
{for(int i=1;i<=maxind;i++)if(in[i]!=out[i])return false;return true;
}
inline void solve2()
{n=read(),m=read();for(int i=1;i<=m;i++){int x=read(),y=read();add(x,y);in[x]++;out[y]++;maxind=max(maxind,max(x,y));}if(!check2())puts("NO");else {dfs2(maxind);if(cnt==m){puts("YES");for(int i=top2;i>=1;i--)cout<<st2[i]-1<<" ";}else puts("NO");}       return;
}inline void dfs1(int now)
{for(int &e=last[now];e;e=before[e]){if(vis[e])continue;int t=e;cnt++;vis[e]=1;vis[e^1]=1;dfs1(to[e]);st[++top]=t;}
}
inline bool check1()
{for(int i=1;i<=maxind;i++)if(in[i]%2)return false;return true;
}
inline void solve1()
{n=read(),m=read();for(int i=1;i<=m;i++){int x=read(),y=read();add(x,y);add(y,x);in[x]++;in[y]++;maxind=max(maxind,max(x,y));}if(!check1())puts("NO");else {dfs1(maxind);if(cnt==m){puts("YES");for(int i=top;i>=1;i--){if(st[i]%2)putchar('-');cout<<(st[i]/2)<<" ";}}else puts("NO");}return;
}int main()
{int t=read();if(t==1)solve1();else solve2();
}

poj1041：求字典序最小的欧拉回路

这道题只说一下怎么求字典序最小。

对于给定的边先按照字母排序，然后从大到小加边，那么访问一个点的边就是从小到大遍历。

Code（代码写得很随意，仅供参考）

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
using namespace std;
const int Maxn=2e3+50;
inline int read()
{char ch=getchar();int i=0,f=1;while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}return i*f;
}int maxind,n,m,o,cnt,ecnt=1,before[Maxn*2],to[Maxn*2],last[Maxn],st[Maxn*2],top,vis[Maxn*2],in[Maxn],out[Maxn];
int st2[Maxn*2],top2,tot,num[Maxn*2];
struct node
{int bg,ed,id,tt;
}edge[Maxn*2];inline bool comp(const node &a,const node &b)
{return a.id>b.id;
}
inline void add(int x,int y,int bz)
{ecnt++;before[ecnt]=last[x];last[x]=ecnt;to[ecnt]=y;num[ecnt]=bz;
}inline void dfs2(int now)
{for(int &e=last[now];e;e=before[e]){if(vis[e])continue;cnt++;int t=e;vis[e]=1;vis[e^1]=1;dfs2(to[e]);st2[++top2]=t;}
}inline bool check2()
{for(int i=1;i<=maxind;i++)if(in[i]%2)return false;return true;
}
int pos;
int main()
{while(n=read(),m=read(),n,m){memset(last,0,sizeof(last));memset(in,0,sizeof(in));memset(out,0,sizeof(out));memset(num,0,sizeof(num));memset(vis,0,sizeof(vis));in[n]++;in[m]++;pos=2000;tot=0;edge[++tot].bg=n;edge[tot].ed=m;edge[tot].id=read();edge[tot].tt=1;edge[++tot].bg=m;edge[tot].ed=n;edge[tot].id=edge[tot-1].id;maxind=max(maxind,max(n,m));ecnt=1;top2=0;cnt=0;maxind=0;o=1;pos=min(n,m);while(n=read(),m=read(),n,m){in[n]++;in[m]++;o++;pos=min(pos,min(n,m));edge[++tot].bg=n;edge[tot].ed=m;edge[tot].id=read();edge[++tot].bg=m;edge[tot].ed=n;edge[tot].id=edge[tot-1].id;maxind=max(maxind,max(n,m));}sort(edge+1,edge+tot+1,comp);for(int i=1;i<=tot;i++){add(edge[i].bg,edge[i].ed,edge[i].id);}if(!check2())puts("Round trip does not exist.");else {dfs2(pos);if(cnt==o){for(int i=top2;i>=1;i--)cout<<num[st2[i]]<<" ";cout<<endl;}else puts("Round trip does not exist.");}}
}

poj1386:Play on Words

题意：
给你n个单词，要求这些单词相连，要求是前面的字母的尾字母和后面单词的头字母相同，问你这n个单词能不能全部连起来，可以连成一条链或者连成一个环。

因为给你n个单词，要每个遍历一遍，很容易想到欧拉图方面的。。
又因为要收尾相连，将26个字母看做顶点，每个单词看成边。
就转化成了给你n条有向边，判断是否能形成欧拉图或者半欧拉图。

不用说，套板。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
const int Maxn=1e5+50;inline int read()
{char ch=getchar();int i=0,f=1;while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}while(isdigit(ch)){i=(i<<1)+(i<<3)+ch-'0';ch=getchar();}return i*f; 
}int n,o,cnt,bg;
int before[Maxn],to[Maxn],last[30],ecnt,in[30],out[30],vis1[30],vt1;
int before2[Maxn*2],to2[Maxn*2],last2[Maxn*2],ecnt2,vis2[30],vt2;
char ch[Maxn];inline void add2(int x,int y)
{ecnt2++;before2[ecnt2]=last2[x];last2[x]=ecnt2;to2[ecnt2]=y;
}inline void add(int x,int y)
{ecnt++;before[ecnt]=last[x];last[x]=ecnt;to[ecnt]=y;
}inline void dfs(int now)
{++cnt;vis2[now]=vt2;for(int e=last2[now];e;e=before2[e]){int v=to2[e];if(vis2[v]!=vt2){dfs(v);}}
}inline bool judge2()
{dfs(bg);if(cnt==o)return true;return false;
}inline bool judge()
{int cnt1=0,cnt1i=0;for(int i=1;i<=30;i++){if(!vis1[i])continue;if(in[i]-out[i]==1)cnt1++;else if(out[i]-in[i]==1)cnt1i++;else if(in[i]!=out[i])return false;}return (cnt1==1&&cnt1i==1)||(cnt1==0&&cnt1i==0);
}int main()
{int T=read();while(T--){vt2++;vt1=o=cnt=bg=0;ecnt=ecnt2=1;memset(vis1,0,sizeof(vis1));memset(last,0,sizeof(last));memset(last2,0,sizeof(last2));memset(in,0,sizeof(in));memset(out,0,sizeof(out));n=read();for(int i=1;i<=n;i++){scanf("%s",ch+1);int len=strlen(ch+1);int x=ch[1]-'a'+1;int y=ch[len]-'a'+1;if(!bg)bg=x;if(!vis1[x])vis1[x]=1,++o;if(!vis1[y])vis1[y]=1,++o;add(x,y);add2(x,y);add2(y,x);in[x]++,out[y]++;}if(judge2()){if(judge())puts("Ordering is possible.");else puts("The door cannot be opened.");}else puts("The door cannot be opened.");}
}

poj2230:求无向图欧拉图（要求每条边走两遍且方向不同）

同样板题，将无向图的边转化为两条有向边，就变成了求有向边欧拉图。

poj2513字符串的欧拉图

其实一样，注意用trie树

poj2337字典序。。

还是排序后加边。。。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<cmath>
using namespace std;
const int Maxn=1e3+50;
int T,n;
string ch[Maxn];int last[30],to[Maxn],before[Maxn],ecnt=1,id[Maxn],fa[30],in[30],out[30],bg,st[Maxn],top,vis[Maxn];struct node
{string s;int id;friend inline bool operator <(const node &a,const node &b){return a.s<b.s;}
}q[Maxn];inline void add(int x,int y)
{++ecnt;before[ecnt]=last[x];last[x]=ecnt;to[ecnt]=y;
}inline int getf(int x)
{if(x==fa[x])return x;return fa[x]=getf(fa[x]);
}inline void dfs(int now)
{for(int &e=last[now];e;e=before[e]){if(vis[e])continue;vis[e]=1;int t=e;dfs(to[e]);st[++top]=t;}
}int bg1,ed1;inline bool check()
{int t=getf(bg);for(int i=1;i<=26;i++){if(!fa[i])continue;bg=min(bg,i);if(getf(i)!=t)return false;}for(int i=1;i<=26;i++){if(in[i]==out[i])continue;else if(in[i]==out[i]-1){if(bg1)return false;bg1=i;}else if(in[i]==out[i]+1){if(ed1)return false;ed1=i;}else return false;}return true;
}int main()
{scanf("%d",&T);while(T--){ecnt=1;bg=0;top=0;bg1=ed1=0;memset(last,0,sizeof(last));memset(fa,0,sizeof(fa));memset(in,0,sizeof(in));memset(out,0,sizeof(out));memset(vis,0,sizeof(vis));scanf("%d",&n);for(int i=1;i<=n;i++){cin>>ch[i];q[i].s=ch[i];q[i].id=i;}sort(q+1,q+n+1);for(int i=n;i>=1;i--){int x=q[i].s[0]-'a'+1,y=q[i].s[q[i].s.size()-1]-'a'+1;if(!fa[x])fa[x]=x;if(!fa[y])fa[y]=y;if(!bg)bg=x;fa[getf(x)]=getf(y);out[x]++;in[y]++;add(x,y);id[ecnt]=q[i].id;}if(check()){if(bg1)dfs(bg1);else dfs(bg);for(int i=top;i>=1;i--){cout<<ch[id[st[i]]];if(i!=1)cout<<".";}cout<<endl;}else puts("***");}
}