欧拉路径和欧拉回路

哥尼斯堡七桥问题

以下内容摘自《信息学奥赛一本通·提高篇》.

欧拉回路问题是图论中最古老的问题之一。它诞生于18世纪的欧洲古城哥尼斯堡，普瑞格尔河流经这座城市，人们在两岸以及河中间的小岛之间建了7座桥，如下图所示：

七桥问题图示

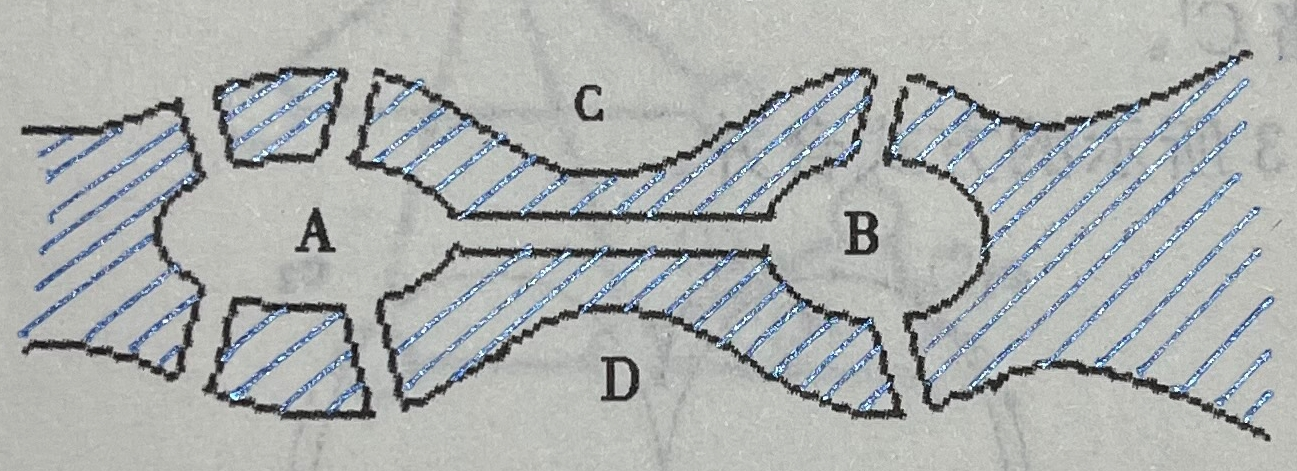
市民们喜欢在这里散步，于是产生了这样一个问题：**是否可以找到一种方案，使得人们从自己家里出发，不重复地走遍每一座桥，然后回到家中？**这个问题如果用数学语言来描述，就是在上图中找出一条回路，使得它不重复地经过每一条边。这便是著名的“哥尼斯堡七桥问题”.

抽象后的图示

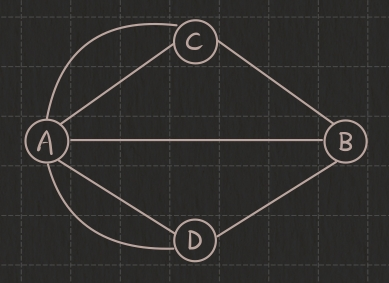
注意：桥是只能走一次，但是点（即小岛和两岸）是可以随便走的.

欧拉路径与欧拉回路

设 $G = (V, E)$ 是一个图.
欧拉路径：图 $G$ 中经过每条边一次并且仅一次的路径称作欧拉路径.
欧拉回路：图 $G$ 中经过每条边一次并且仅一次的回路称作欧拉回路.

欧拉路径问题也被称为一笔画问题.

性质与定理：

假设某图满足欧拉路径，则讨论图中点的度数（无向图，直接将点的连边数作为度数）：

对于起点来说，其作为起始点往外走度数 $+ 1$ ，之后如果每次经过起点，应该立刻再走出去（走回来就停住就变成欧拉回路了）度数 $+ 2$ ，所以起点的度数应为奇数；
对于终点同理，终点的度数应为奇数；
对于中间点来说，经过此点就应该立即再走出去，度数 $+ 2$ ，故中间点的度数应为偶数.

特殊地，当起点与终点为同一个点时，此点度数显然为偶数，当然，此时形成的是欧拉回路；
可以说欧拉回路是特殊的欧拉路径.

如上可以得出度数为奇数的点只有能 $0$ 或 $2$ 个是存在欧拉路径的必要条件 .

对于无向联通图

存在欧拉路径的充分必要条件：度数为奇数的点只有能 $0$ 或 $2$ 个；
存在欧拉回路的充分必要条件：度数为奇数的点只能有 $0$ 个.

对于有向联通图

类比无向图.
实际上对于中间点，入度与出度相等即可.
对于起点，出度比入度多一；
对于终点，入度比出度多一；
特殊地，当起点与终点为同一点，则其入度与出度也相等.

存在欧拉路径的充分必要条件：要么所有点的出度均等于入度；要么除了两个点之外，其余所有点的出度等于入度，剩余的两个点，一个满足出度比入度多一，另一个满足入度比出度多一；
存在欧拉回路的充分必要条件：所有点的出度均等于入度.

充分性证明

如上只证明了存在欧拉路径或欧拉回路能推出如上的结论，但这仅仅代表结论是存在欧拉路径或欧拉回路的必要条件，仍需证明其充分性.

现在需要证明，如上的结论本身能够推出其构成的图都是欧拉路径或欧拉回路：

对于有一个公共点的一个环和一条线段组成的图，显然存在欧拉路径；同样地对于有一个公共点的两个环，显然存在欧拉回路.

两种情况图示

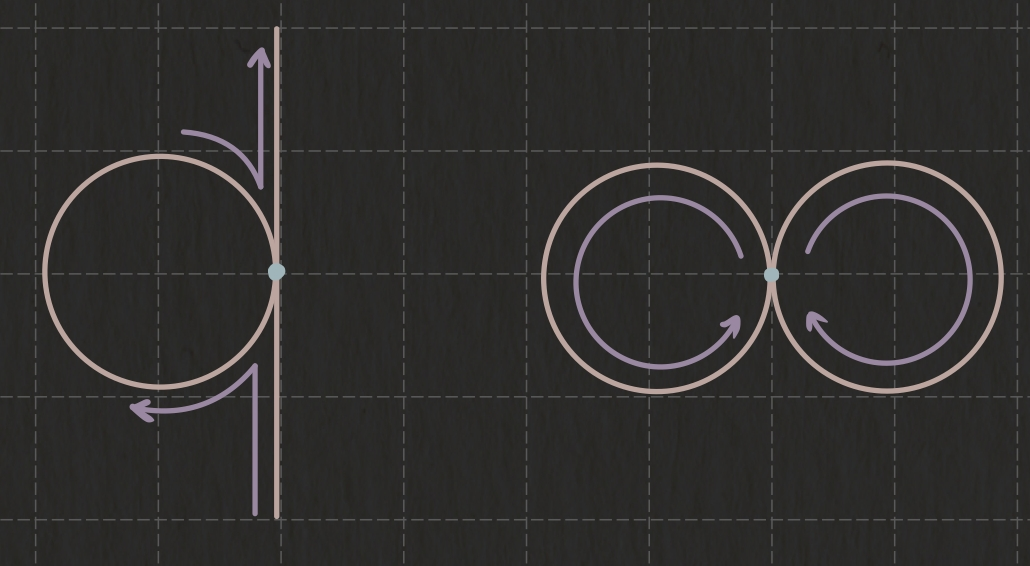
更普遍地想，如果无向联通图满足度数为奇数的点只有 $2$ 个的话，从某个度数为奇数的点开始进行深度优先遍历，那么除了起点与终点之外，走到中间点时，由于其度数为偶数，到达中间点时就必然会存在另外一条没有走过的边往外走.

但可能存在搜到终点时，并没有将整个图都遍历完的情况.
这时深度优先搜索的回溯就可以将搜到终点时没有遍历到的点都再遍历到；

另一种理解方式就是，在遍历过程中，终点是有可能先被遍历到的，但这不并影响整个图都被遍历到；
那么都遍历过终点了，深度优先遍历什么时候才会停止呢？实际上如果存在上述情况，实际上当所有公共点所共用的环都被遍历完，搜索就会停止，停止在公共点上，然后再往上回溯到起点.

故欧拉路径实际上可以看作一条线段路径上，有很多与其有公共点的环和与环有公共点的环.
其他结论的证明方式是类似的，有了如上的证明也是显然的了.

有向联通图也不难想，实际上就是把度数作为区分，对于中间点，有入度就一定有对应的出度.

这样就证明了充分性.

Q：对于有向联通图来说，从中间点出发，一定会有一条回来的边，但出发的路径是否一定会走回出发的中间点呢？

A：这是不可能的，因为从中间点出发，由于其入度与出度相同，所以只要有一条没有走过的入边，就一定有一条对应的没走过的出边；因为图联通且点的个数有限，所以一定可以在有限步内走回出发的中间点.

算法过程

假设现有一张无向连通图，图中只存在两个度数为奇数的点.

从起点出发，没有回溯时的第一条路径，必然会走到终点.

从起点出发的话，一旦出发之后，把所有已经用过的边删掉后，在剩下的图中，对于任何一个不是终点的结点来说（包括起点），度数都是偶数，因此第一条路径走到了某个点上的话，由于此点的度数为偶数，则必然会存在一条能出去的边；
但这个过程不可能是无限的，因为边的数量是有限的，因此最终必然会在终点的位置停止.

这样中间的道路会有很多个环，可以使用以下伪代码的顺序填入序列当中：

dfs(u){for 从u出发的所有边dfs() //扩展seq <- u //将 u 加入到序列当中
}

当搜完所有和 $u$ 相关的点之后，就可以认为从 $u$ 出发往后遍历到终点的所有的点都已经加入了序列当中，此时也就可以将 $u$ 也放入序列当中了.
序列储存的是一种欧拉回路的倒序走法，只需要逆序输出就可以了.

欧拉路径从一个度数为奇数的点开始搜；欧拉回路可以从任意点开始搜.

细节

一般的 $D F S$ 会用点来判重，时间复杂度为 $O (n + m)$ .

欧拉回路问题是用边来判重，如果图是一个点但有 $m$ 条自己指向自己的自环重边，则对于欧拉回路来说，走法序列长度为 $m$ ，而每次都要遍历 $m$ 条边是否可走，故时间复杂度可能会达到 $O(m^2)$ .

这样对欧拉回路时 $D F S$ 的优化即为：在经过某一条边时，不是简单地把这条边标记一下，而是把它直接删掉，这样就可以保证每用一条边就会删一条边，每条边就只会被用一次，这样时间复杂度就可以降为 $O (n + m)$ .

有些题目可能因为使用了随机数据，不加优化可能也可以过；但如果出题人有意卡的话，是很可能卡住的.

如果是有向图的话，每用一条边删掉就可以了；如果是无向图的话，因为每条边建的时候需要建两个方向，所以删边时不能忘记相对应的另一条边，需要同时删掉.

如果边的编号从 $0$ 开始，那么建边时 $(0,1),(2,3),(4,5),\cdots$ 都是对应的一组边，可以发现 $\;xor\; 1$ （异或）即为编号为 $u$ 的边的对应边.

AcWing 1123. 铲雪车

原题链接

随着白天越来越短夜晚越来越长，我们不得不考虑铲雪问题了。

整个城市所有的道路都是双向车道，道路的两个方向均需要铲雪。因为城市预算的削减，整个城市只有 $1$ 辆铲雪车。

铲雪车只能把它开过的地方（车道）的雪铲干净，无论哪儿有雪，铲雪车都得从停放的地方出发，游历整个城市的街道。

现在的问题是：最少要花多少时间去铲掉所有道路上的雪呢？

输入格式

输入数据的第 $1$ 行表示铲雪车的停放坐标 $(x, y) ， x, y$ 为整数，单位为米。

下面最多有 $4000$ 行，每行给出了一条街道的起点坐标和终点坐标，坐标均为整数，所有街道都是笔直的，且都是双向车道。

铲雪车可以在任意交叉口、或任何街道的末尾任意转向，包括转 $U$ 型弯。

铲雪车铲雪时前进速度为 $20$ 千米/时，不铲雪时前进速度为 $50$ 千米/时。

保证：铲雪车从起点一定可以到达任何街道。

输出格式

输出铲掉所有街道上的雪并且返回出发点的最短时间，精确到分钟，四舍五入到整数。

输出格式为 hours:minutes，minutes 不足两位数时需要补前导零。

具体格式参照样例。

数据范围

$10^6≤x,y≤10^6$

所有位置坐标绝对值不超过 $10^6$ 。

输入样例：

0 0
0 0 10000 10000
5000 -10000 5000 10000
5000 10000 10000 10000

输出样例：

3:55

样例解释

输出结果表示共需 $3$ 小时 $55$ 分钟。

时/空限制： 1s / 64MB
来源：《信息学奥赛一本通》
算法标签：欧拉回路

yxc’s Solution

因为街道都是双向车道，所以每个街道的起点和终点的入度和出度都对应 $+ 1$ ，因此可以发现所有点的入度和出度都是相等的，此图必然存在欧拉回路.
因为铲雪车必然在某个街道上，故由于此图存在欧拉回路，不管从哪个点开始，都一定可以每条边不重复地回到起点.
因此其最短时间即为所有边长度的二倍 $2 l$ 再除以铲雪时的速度 $20 k m / h$ ，注意转化时间.

因此此题实际上只是利用了欧拉回路的性质，甚至不需要使用欧拉回路的算法，定理和代码不一定有相关性，并不是说代码没有在这道题出现，这道题就和算法不相关.

可以发现，起点坐标是没有任何意义的（保证铲雪车在道路上）.

#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int main(){double x1,y1,x2,y2;cin>>x1>>y1;double sum=0;while(cin>>x1>>y1>>x2>>y2){double dx=x1-x2;double dy=y1-y2;sum+=sqrt(dx*dx+dy*dy)*2;}int minutes=round(sum/1000/20*60);int hours=minutes/60;minutes%=60;printf("%d:%02d",hours,minutes);return 0;
}

AcWing 1184. 欧拉回路

原题链接

给定一张图，请你找出欧拉回路，即在图中找一个环使得每条边都在环上出现恰好一次。

输入格式

第一行包含一个整数 $t，t∈{1,2}$ ，如果 $t = 1$ ，表示所给图为无向图，如果 $t = 2$ ，表示所给图为有向图。

第二行包含两个整数 $n, m$ ，表示图的结点数和边数。

接下来 $m$ 行中，第 $i$ 行两个整数 $v_i,u_i$ ，表示第 $i$ 条边（从 $1$ 开始编号）。

如果 $t = 1$ 则表示 $v_i$ 到 $u_i$ 有一条无向边。
如果 $t = 2$ 则表示 $v_i$ 到 $u_i$ 有一条有向边。

图中可能有重边也可能有自环。

点的编号从 $1$ 到 $n$ 。

输出格式

如果无法一笔画出欧拉回路，则输出一行：NO。

否则，输出一行：YES，接下来一行输出 任意一组 合法方案即可。

如果 $t = 1$ ，输出 $m$ 个整数 $p_1,p_2,…,p_m$ 。令 $e=|p_i|$ ，那么 $e$ 表示经过的第 $i$ 条边的编号。如果 $p_i$ 为正数表示从 $v_e$ 走到 $u_e$ ，否则表示从 $u_e$ 走到 $v_e$ 。
如果 $t = 2$ ，输出 $m$ 个整数 $p_1,p_2,…,p_m$ 。其中 $p_i$ 表示经过的第 $i$ 条边的编号。

数据范围

$1≤n≤10^5$ ,
$0≤m≤2×10^5$

输入样例1：

输出样例1：

YES
1 2 -3

输入样例2：

输出样例2：

YES
4 1 3 5 2 6

时/空限制： 1s / 64MB
来源：《信息学奥赛一本通》
算法标签：欧拉回路

yxc’s Solution

这道题的一个问题是：怎么判断无解？
什么样的图存在欧拉回路？

无向图

所有点的度数必须都为偶数；
所有边都联通（这道题没有要求点联通）.

有向图

所有点的入度等于出度；
所有边都联通.

无向图也是用入度与出度，因为使用时是将入度与出度相加，即为度数，故可以直接使用.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010,M=400010;
int type;
int n,m;
int h[N],e[M],ne[M],idx;
bool used[M];
int ans[M>>1],cnt; //因为无向图边扩了一倍，但答案不需要，所以这里除以二
int din[N],dout[N];
void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u){//这里不能写 for(int i=h[u];~i;i=ne[i]) 而是写成现在的样子 //因为 删边实际上只是在修改 h[u] 的值，但是 i 本身还是在遍历//如果遇到自环的情况还是遍历完所有边，从而被卡成 O(m^2) 故需要更改写法//这里的写法等同于每次删掉离 h[u] 最近的那条边for(int &i=h[u];~i;){if(used[i]){i=ne[i]; //一旦用过一条边，就把它删掉continue;}used[i]=true;if(type==1) used[i^1]=true;//记录边的编号int t;if(type==1){t=i/2+1;if(i & 1) t=-t;} else t=i+1;int v=e[i];i=ne[i];dfs(v);ans[++cnt]=t;}
}
int main(){scanf("%d",&type);scanf("%d %d",&n,&m);memset(h,-1,sizeof h);for(int i=0;i<m;++i){int a,b;scanf("%d %d",&a,&b);add(a,b);if(type==1) add(b,a);din[b]++,dout[a]++;}//对于条件1. 的判断if(type==1){for(int i=1;i<=n;++i)if(din[i]+dout[i] &1){puts("NO");return 0;}} else {for(int i=1;i<=n;++i)if(din[i]!=dout[i]){puts("NO");return 0;}}//因为只要求边联通，不要求点联通，故找到第一个不孤立点for(int i=1;i<=n;++i)if(h[i]!=-1){dfs(i);break;}//判断遍历到的边的数量和m是不是相等的if(cnt<m){puts("NO");return 0;}puts("YES");for(int i=cnt;i;--i) printf("%d ",ans[i]);return 0;
}

AcWing 1124. 骑马修栅栏

题目链接

农民 $J o h n$ 每年有很多栅栏要修理。

他总是骑着马穿过每一个栅栏并修复它破损的地方。

$J o h n$ 是一个与其他农民一样懒的人。

他讨厌骑马，因此从来不两次经过一个栅栏。

你必须编一个程序，读入栅栏网络的描述，并计算出一条修栅栏的路径，使每个栅栏都恰好被经过一次。

$J o h n$ 能从任何一个顶点（即两个栅栏的交点）开始骑马，在任意一个顶点结束。

每一个栅栏连接两个顶点，顶点用 $1$ 到 $500$ 标号（虽然有的农场并没有 $500$ 个顶点）。

一个顶点上可连接任意多（ $\geq 1$ ）个栅栏。

所有栅栏都是连通的（也就是你可以从任意一个栅栏到达另外的所有栅栏）。

你的程序必须输出骑马的路径（用路上依次经过的顶点号码表示）。

我们如果把输出的路径看成是一个 $500$ 进制的数，那么当存在多组解的情况下，输出 $500$ 进制表示法中最小的一个（也就是输出第一个数较小的，如果还有多组解，输出第二个数较小的，等等）。

输入数据保证至少有一个解。

输入格式

第 $1$ 行：一个整数 $F$ ，表示栅栏的数目;

第 $2$ 到 $F + 1$ 行：每行两个整数 $i, j$ 表示这条栅栏连接 $i$ 与 $j$ 号顶点。

输出格式

输出应当有 $F + 1$ 行，每行一个整数，依次表示路径经过的顶点号。

注意数据可能有多组解，但是只有上面题目要求的那一组解是认为正确的。

数据范围

$1 \leq F \leq 1024$ ,
$1 \leq i, j \leq 500$

输入样例：

输出样例：

时/空限制： 1s / 64MB
来源：《信息学奥赛一本通》 , usaco training 3.3
算法标签：欧拉路径

yxc’s Solution

这道题需要考虑如何输出欧拉序字典序最小的解？

dfs(int u){for u 的所有出边dfs(v)seq <-u
}

对于 $u$ 这个点来说，一旦从 $u$ 走出去之后，必然还会回来，所以 $u$ 这个点一定会出现在 $s e q$ 的尾部；
这样 $s e q$ 的逆序之中， $u$ 就一定会出现在开头；
所以，只需要保证 $u$ 的出边的点的编号从小到大遍历即可.

对边排序太过麻烦，而且点数有较小，可以使用邻接矩阵来储存.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=510,M=2100;
int n=500,m;
int g[N][N];
int ans[M>>1],cnt;
int d[N];
void dfs(int u){for(int i=1;i<=n;++i)if(g[u][i]){--g[u][i],--g[i][u];dfs(i);}ans[++cnt]=u;
}
int main(){cin>>m;while(m--){int a,b;cin>>a>>b;g[a][b]++,g[b][a]++;d[a]++,d[b]++;}int start=1;while(!d[start]) ++start;for(int i=1;i<=n;++i)if(d[i]&1){start=i;break;}dfs(start);for(int i=cnt;i;--i) printf("%d\n",ans[i]);return 0;
}

AcWing 1185. 单词游戏

原题链接

有 $N$ 个盘子，每个盘子上写着一个仅由小写字母组成的英文单词。

你需要给这些盘子安排一个合适的顺序，使得相邻两个盘子中，前一个盘子上单词的末字母等于后一个盘子上单词的首字母。

请你编写一个程序，判断是否能达到这一要求。
输入格式

第一行包含整数 $T$ ，表示共有 $T$ 组测试数据。

每组数据第一行包含整数 $N$ ，表示盘子数量。

接下来 $N$ 行，每行包含一个小写字母字符串，表示一个盘子上的单词。

一个单词可能出现多次。

输出格式

如果存在合法解，则输出 Ordering is possible.，否则输出 The door cannot be opened.。

数据范围

$1≤N≤10^5$ ,
单词长度均不超过 $1000$

输入样例：

3
2
acm
ibm
3
acm
malform
mouse
2
ok
ok

输出样例：

The door cannot be opened.
Ordering is possible.
The door cannot be opened.

时/空限制： 1s / 64MB
来源：《信息学奥赛一本通》
算法标签：欧拉路径

yxc’s Solution

每个单词看成一条边，首尾字母看作点，这样问题就转化为了一张有向图；
问题就变为了有向图是否存在欧拉路径：

除了起点、终点外，其余点的入度等于出度；
图是否联通.

连通性可以用并查集来维护.

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=30;
int n,m;
int din[N],dout[N],p[N];
bool st[N];
int find(int x){if(p[x]!=x) p[x]=find(p[x]);return p[x];
}
int main(){char str[1010];int T; scanf("%d",&T);while(T--){scanf("%d",&n);memset(din,0,sizeof din);memset(dout,0,sizeof dout);memset(st,0,sizeof st);for(int i=0;i<26;++i) p[i]=i;for(int i=0;i<n;++i){scanf("%s",str);int len=strlen(str);int a=str[0]-'a',b=str[len-1]-'a';st[a]=st[b]=true;dout[a]++,din[b]++;p[find(a)]=find(b);}int start=0,end=0;bool success=true;//找到起点与终点for(int i=0;i<26;++i)if(din[i]!=dout[i]){if(din[i]==dout[i]+1) end++;else if(din[i]+1==dout[i]) start++;else{success=false;break;}}//只有 起点终点都不存在 或者 起点终点都只有一个 才可行if(!((!start && !end) ||(start==1 && end==1))) success=false;//判断图是否联通int rep=-1;for(int i=0;i<26;++i)if(st[i]){if(rep==-1) rep=find(i);else if(rep!=find(i)){success=false;break;}}if(success) puts("Ordering is possible.");else puts("The door cannot be opened.");}return 0;
}