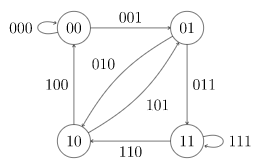
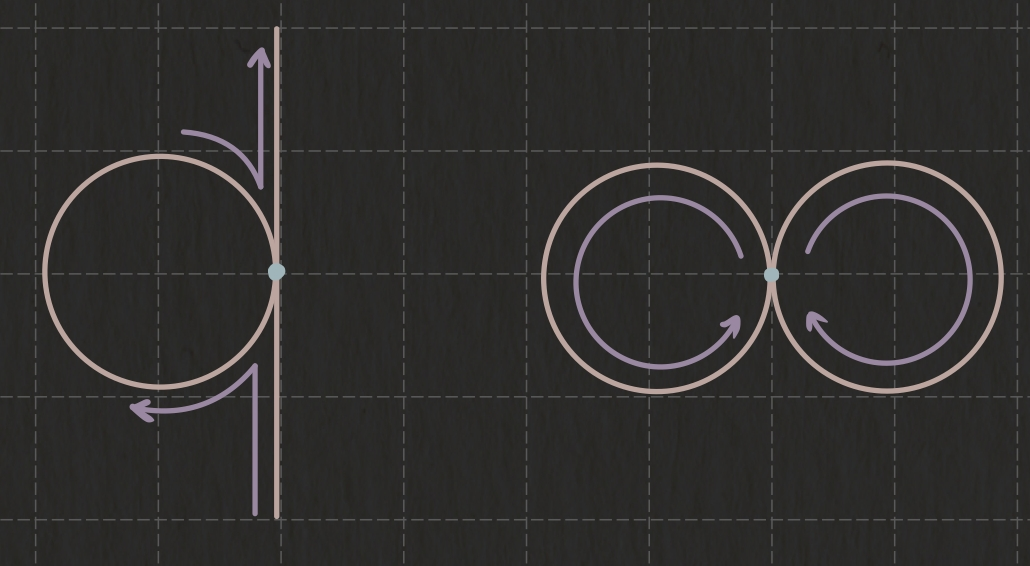欧拉回路（Euler circuit）

如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径

如果一个回路是欧拉路径，则称为欧拉回路

具有欧拉回路的图称为欧拉图（简称ë图），具有欧拉路径但不具有欧拉回路的图称为半欧拉图

欧拉定理

1）欧拉路：通过图中所有边的简单路

2）欧拉回路：闭合的欧拉路

3）欧拉图：包含欧拉回路的图

无向图存在欧拉回路的充要条件

一个无向图存在欧拉回路，当且仅当该图所有顶点度数都为偶数，且该图是连通图

有向图存在欧拉回路的充要条件

一个有向图存在欧拉回路，除2个端点外其余节点入度=出度；1个端点入度比出度大1；一个端点入度比出度小1或所有节点入度等于出度且该图是连通图。

混合图存在欧拉回路条件

要判断一个混合图G（V，E）（既有有向边又有无向边）是欧拉图，方法如下：

假设有一张图有向图G '在不论方向的情况下它与G同构。并且G' 包含了G的所有有向边。那么如果存在一个图G '使得G' 存在欧拉回路，那么G就存在欧拉回路。

其思路就将混合图转换成有向图判断。实现的时候，我们使用网络流的模型。现任意构造一个G'。用Ii表示第i个点的入度，Oi表示第i个点的出度。如果存在一个点k，|Ok-Ik|mod 2=1，那么G不存在欧拉回路。接下来则对于所有Ii>Oi的点从源点连到i一条容量为(Ii-Oi)/2的边，对于所有Ii<Oi的点从i连到汇点一条容量为(Oi-Ii)/2的边。如果对于节点U和V，无向边（U，V）∈E，那么U和V之间互相建立容量为1的边。如果此网络的最大流等于∑|Ii-Oi|/2，那么就存在欧拉回路

判断连通：并查集

什么是连通：连通图基于连通的概念。在一个无向图G中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。如果G是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。（不是任意两点都需要有直接路径）

无向图欧拉回路 eg：HDU 1878(欧拉回路）

#include<stdio.h>
#include<memory.h>
#include<iostream>
#define MAX 1005
using namespace std;
int pre[MAX];
int in[MAX];
int M, N;
void init(){    //并查集初始化操作for(int i = 1; i <= N; ++i){pre[i] = i;}
}
int find(int x){    //并查集查找操作int r = x;while(r != pre[r]){r = pre[r];}int i = x, j;while(i != r){j = pre[i];pre[i] = r;i = j;}return r;
}
void join(int a, int b){    //并查集合并操作int x = find(a);int y = find(b);if(x != y)pre[a] = b;
}
int main(){while(scanf("%d", &N) && N){scanf("%d", &M);int a, b;memset(pre, 0, sizeof(pre));memset(in, 0, sizeof(in));init();for(int i = 0; i < M; ++i){scanf("%d%d", &a, &b);join(a, b);in[a]++;in[b]++;}int flag1 = 0, flag2 = 0;for(int i = 1; i <= N; ++i){    //判断是否连通if(pre[i] == i){flag2++;}}for(int i = 1; i <= N; ++i){    //判断一个顶点的度是否为偶数if(in[i] % 2){flag1 = 1;break;}}if(flag1 == 1 || flag2 - 1 != 0)printf("0\n");elseprintf("1\n");}
}

有向图欧拉回路：eg HDU 1116（Play on Words）

#include<stdio.h>
#include<iostream>
#include<memory.h>
using namespace std;
#define MAX 1005
int pre[MAX];
int in[MAX], out[MAX],existed[MAX];
//有向欧拉回路：连通且每个顶点入度等于出度
void init(){for(int i = 1; i <= 26; ++i){pre[i] = i;}
}
int find(int x){int r = x;while(r != pre[r]){r = pre[r];}int i = x, j;while(i != r){j = pre[i];pre[i] = r;i = j;}return r;
}
void join(int a, int b){int x = find(a);int y = find(b);if(x != y){pre[x] = y;}
}
int main(int argc, char const *argv[])
{int T;scanf("%d", &T);char ch[MAX];while(T--){memset(pre, 0, sizeof(pre));memset(in, 0, sizeof(in));memset(out, 0, sizeof(out));memset(existed, 0, sizeof(existed));memset(ch, 0, sizeof(ch));init();int n;cin>>n;for(int i = 1;i <= n; ++i){cin>>ch;int a = ch[0] - 'a' + 1;  //将字符转换成整型int b = ch[strlen(ch) - 1] - 'a' + 1;join(a, b);   //并查集out[a]++;in[b]++;existed[a] = 1;   //表示在这个输入里有这个字母existed[b] = 1;}int ans = 0;for(int i = 1; i <= 26; ++i){if(pre[i] == i && existed[i] == 1)ans++;  //查询路径是否连通}if(ans > 1){printf("The door cannot be opened.\n");continue;}int input = 0, output = 0, middle = 0;// 头： 出度 = 入度 + 1    尾：入度 = 出度 + 1   中间：出度 == 入度for(int i = 1; i <= 26; ++i){if((in[i] != out[i]) && existed[i]){if(in[i] == out[i] + 1){input++;}else if(in[i] + 1 == out[i]){output++;}elsemiddle++;}}if(middle){printf("The door cannot be opened.\n");continue;}if((input == 1 && output == 1) || (input == 0 && output == 0)){printf("Ordering is possible.\n");continue;}elseprintf("The door cannot be opened.\n");}return 0;
}