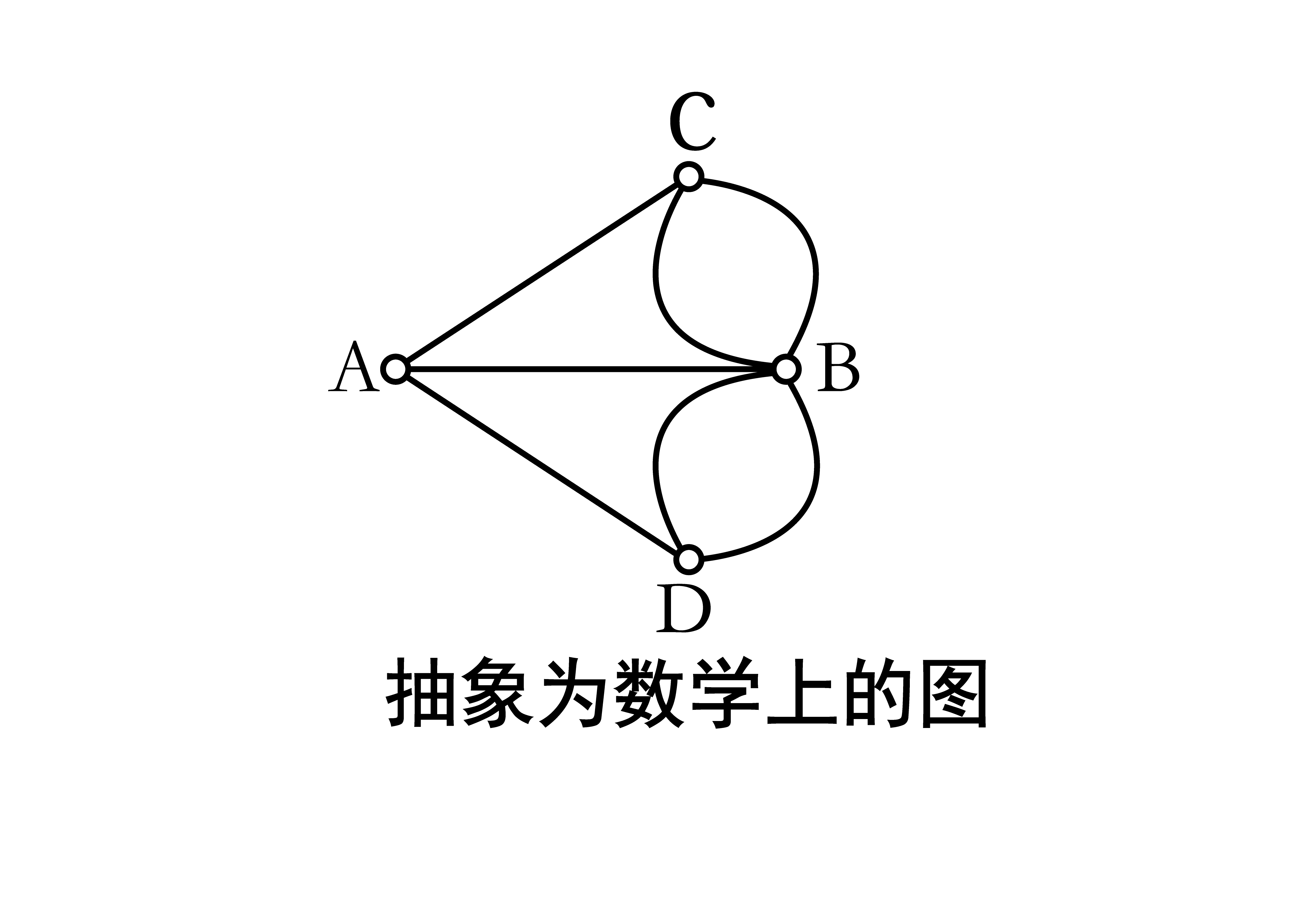
欧拉回路相关定义:
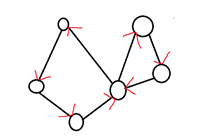
|| 如果图G(有向图或者无向图)中有一条通路,该通路上所有边一次且仅有一次行遍所有顶点,那么这条通路称为欧拉通路
|| 如果图G中所有边一次且仅有一次行遍所有顶点,称图G有欧拉回路
|| 具有欧拉回路的图称为欧拉图,不具有欧拉回路但具有欧拉通路的图称为半欧拉图
欧拉回路的定理和推论:
|| 无向图G存在欧拉通路的充要条件为: G为连通图,且G有0或2个奇度节点( 度数为奇度的节点)
|| 推论1:当无向图G只有两个奇度节点时,那么其中的欧拉通路以这两个节点为端点
|| 推论2:当无向图G没有奇度节点时,那么G必有欧拉回路
|| 推论3:无向图G为欧拉图的充要条件是:G为连通图,且G有0个奇度节点
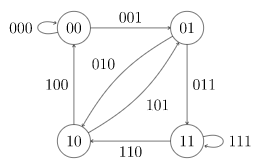
|| 有向图G存在欧拉通路的充要条件为:(为了好记忆把出度入度不相等的点命名为“异点”)
D为有向图,D的基图连通,并且所有顶点的出度与入度都相等;或者除两个顶点外,其余顶点的出度与入度都相等,而这两个顶点中一个顶点的出度与入度之差为1,另一个顶点的出度与入度之差为-1。
|| 简化:D为连通有向图,且有0个或者2个异点(且这两两个异点的出入度差分别为±1)
|| 推论1: 当D除出、入度之差为1,-1的两个顶点之外,其余顶点的出度与入度都相等时,D的有向欧拉通路必以出、入度之差为1的顶点作为始点,以出、入度之差为-1的顶点作为终点。
|| 推论2: 当D的所有顶点的出、入度都相等时,D中存在有向欧拉回路。
|| 推论3: 有向图D为有向欧拉图的充分必要条件是D的基图为连通图,并且所有顶点的出、入度都相等。
欧拉回路的求解
|| DFS搜索求解欧拉回路:
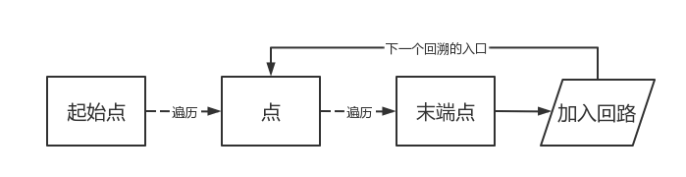
基本思路:利用欧拉定理判断出一个图存在欧拉回路或欧拉通路后,选择一个正确的起始顶点,用DFS算法遍历所有的边(每一条边只遍历一次),遇到走不通就回退。在搜索前进方向上将遍历过的边按顺序记录下来。这组边的排列就组成了一条欧拉通路或回路。
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int ans[200];
int top;
int N,M;
int mp[200][200];
void dfs(int x)
{int i;top++;ans[top]=x;for (i=1; i<=N; i++){if(mp[x][i]>0){mp[x][i]=mp[i][x]=0;///删除此边dfs(i);break;}}
}void fleury(int x)
{int brige,i;top=1;ans[top]=x;///将起点放入Euler路径中while(top>=0){brige=0;for (i=1; i<=N; i++) /// 试图搜索一条边不是割边(桥){if(mp[ans[top]][i]>0)///存在一条可以扩展的边{brige=1;break;}}if (!brige)/// 如果没有点可以扩展,输出并出栈{printf("%d ", ans[top]);top--;}else /// 否则继续搜索欧拉路径{top--;///为了回溯dfs(ans[top+1]);}}
}int main()
{int x,y,deg,num,start,i,j;scanf("%d%d",&N,&M);memset(mp,0,sizeof (mp));for(i=1;i<=M; i++){scanf("%d%d",&x,&y);mp[x][y]=1;mp[y][x]=1;}num=0;start=1;///这里初始化为1for(i=1; i<=N; i++){deg=0;for(j=1; j<=N; j++){deg+=mp[i][j];}if(deg%2==1)///奇度顶点{start=i;num++;}}if(num==0||num==2){fleury(start);}else{puts("No Euler path");}return 0;
}
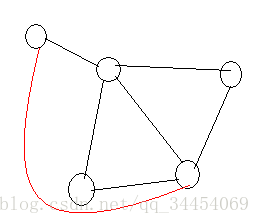
|| Fleury(佛罗莱)算法:(算法的关键是:能不走桥就不去走桥,实在无路可走了才去走桥)

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int ans[200];
int top;
int N,M;
int mp[200][200];
void dfs(int x)
{int i;top++;ans[top]=x;for (i=1; i<=N; i++){if(mp[x][i]>0){mp[x][i]=mp[i][x]=0;///删除此边dfs(i);break;}}
}void fleury(int x)
{int brige,i;top=1;ans[top]=x;///将起点放入Euler路径中while(top>=0){brige=0;for (i=1; i<=N; i++) /// 试图搜索一条边不是割边(桥){if(mp[ans[top]][i]>0)///存在一条可以扩展的边{brige=1;break;}}if (!brige)/// 如果没有点可以扩展,输出并出栈{printf("%d ", ans[top]);top--;}else /// 否则继续搜索欧拉路径{top--;///为了回溯dfs(ans[top+1]);}}
}int main()
{int x,y,deg,num,start,i,j;scanf("%d%d",&N,&M);memset(mp,0,sizeof (mp));for(i=1;i<=M; i++){scanf("%d%d",&x,&y);mp[x][y]=1;mp[y][x]=1;}num=0;start=1;///这里初始化为1for(i=1; i<=N; i++){deg=0;for(j=1; j<=N; j++){deg+=mp[i][j];}if(deg%2==1)///奇度顶点{start=i;num++;}}if(num==0||num==2){fleury(start);}else{puts("No Euler path");}return 0;
}