http://www.cnblogs.com/pandy/archive/2009/05/07/1452209.html

 

参考以上：

 

判断欧拉路，欧拉回路：

注意图联通，可以DFS或者并查集

一．无向图

欧拉回路：每个顶点度数都是偶数

欧拉路：所有点度数为偶数，或者只有2个点度数为奇数

二．有向图（非混合）

欧拉回路：每个顶点入度等于出度

欧拉路：每个顶点入度等于出度；

或者只有1个点入度比出度小1, 从这点出发，只有1个点出度比入度小1，从这个点结束，其他点入度等于出度

三．混合图（有的边单向，有的边不确定方向）

 

欧拉回路：　　

 

判断一个图中是否存在欧拉回路（每条边恰好只走一次，并能回到出发点的路径），在以下三种情况中有三种不同的算法：

一、无向图
每个顶点的度数都是偶数，则存在欧拉回路。

二、有向图（所有边都是单向的）
每个节顶点的入度都等于出度，则存在欧拉回路。

 

 

欧拉路：

首先判断底图是否联通；

然后，给不定向边 随便给定方向，考虑每个点的出度和入度：

1）如果入度和出度之差 都是偶数，说明如果存在欧拉路，则一定是欧拉回路，解法同上；

2）如果可以找到一个且仅一个点st，入度比出度 小奇数，一个出度比入度小奇数的点ed，则加无向边(st，ed), 转为混合图欧拉回路问题

 

另外，一般关于欧拉路的题，边数都比较少，如果要求字典序最小，则可以直接存边，排序后，每次dfs，先走小的，这样记录结束顺序，倒叙输出，就是字典序最小的。因为倒叙输出，先遍历到的点会先输出。

混合图欧拉回路  相关题目：pku1637，zju1992，hdu3472
　　混合图欧拉回路用的是网络流。
　　把该图的无向边随便定向，计算每个点的入度和出度。如果有某个点出入度之差为奇数，那么肯定不存在欧拉回路。因为欧拉回路要求每点入度 = 出度，也就是总度数为偶数，存在奇数度点必不能有欧拉回路。
　　好了，现在每个点入度和出度之差均为偶数。那么将这个偶数除以2，得x。也就是说，对于每一个点，只要将x条边改变方向（入>出就是变入，出>入就是变出），就能保证出 = 入。如果每个点都是出 = 入，那么很明显，该图就存在欧拉回路。
　　现在的问题就变成了：我该改变哪些边，可以让每个点出 = 入？构造网络流模型。首先，有向边是不能改变方向的，要之无用，删。一开始不是把无向边定向了吗？定的是什么向，就把网络构建成什么样，边长容量上限1。另新建s和t。对于入 > 出的点u，连接边(u, t)、容量为x，对于出 > 入的点v，连接边(s, v)，容量为x（注意对不同的点x不同）。之后，察看是否有满流的分配。有就是能有欧拉回路，没有就是没有。欧拉回路是哪个？查看流值分配，将所有流量非 0（上限是1，流值不是0就是1）的边反向，就能得到每点入度 = 出度的欧拉图。
　　由于是满流，所以每个入 > 出的点，都有x条边进来，将这些进来的边反向，OK，入 = 出了。对于出 > 入的点亦然。那么，没和s、t连接的点怎么办？和s连接的条件是出 > 入，和t连接的条件是入 > 出，那么这个既没和s也没和t连接的点，自然早在开始就已经满足入 = 出了。那么在网络流过程中，这些点属于“中间点”。我们知道中间点流量不允许有累积的，这样，进去多少就出来多少，反向之后，自然仍保持平衡。
　　所以，就这样，混合图欧拉回路问题，解了。

 

 

 

 

1 HDU 3018 Ant Trip

          一笔画问题，无向图欧拉路或者欧拉回路，注意题目说了，如果是孤立点，则不用考虑。

   对于每个连通块，如果全都是偶数度，则需要1笔；如果不是，则需要奇数度顶点个数的1/2笔。   我用并查集写的。

 

 

2 POJ 1041 John's trip

   

       题目给了一个图，街道编号1..n(n<1995), 点编号1..m(m<44),求欧拉回路

且字典序最小

     关于字典序最小，每次dfs，先走最小的，这样倒叙输出时 先dfs到的先输出

比较好的是实现是 直接按编号存边，dfs 记录结束序，倒叙输出

fill() [1,m] 忘加1了，WA了几次

 

 

3 POJ 1386 Play on Words

   貌似很经典的模型了，应该叫 单词接龙吧。

   本题要求判断是否有 有向图欧拉路

 

 

4 POJ 2230 Watch Cow

    题目描述每条路必须走两次，且方向不同，其实一样了，有向图的欧拉回路

不过需要输出的是路径中的节点。

 

void dfs(int u) {int i;for (i = head[u]; i != -1; i = edge[i].pre) {if (!edge[i].flg)  {edge[i].flg = 1;dfs(edge[i].v);printf ("%d\n", edge[i].v);}}}

 

 

 

 

5 POJ 2513 Colored Sticks

   比较简单，判定是否存在 无向图欧拉路

 

 

6 POJ 2337 Catenyms

   还是单词 首尾相连，要求判断，然后输出字典序最小的

   有向图欧拉路，字典序最小，把单词按照字典序排序，优先dfs小的，记录结束序，倒叙输出即可。

没写break，查了好久

 

 

7 POJ 1392 Ouroboros Snake

http://blog.csdn.net/yueashuxia/archive/2010/07/12/5729878.aspx

 

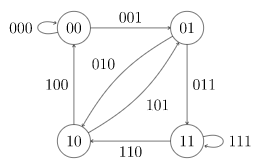
   这里涉及到DeBruijin图，即当k=3 时，我们构造一个0，1构成的环，长度为 2^k，其中，任意的连续的长度为k个的，会组成0，2^k-1的所有的数字刚好一次，而且要求换的字典序最小。   这里关键就是建图了，取k-1长度的串，一共有2^(k-1)个作为点，如果我们把这个串左移,末尾加1或0，可以得到新的节点，则连有向边，共有2^k条边，求欧拉回路，字典序最小即可。

    本题要求 按顺序输出 组成的数字。

8 HDU 2894 DeBruijin

     同上，这次要输出串