目录

一、链表的中间结点

二、回文链表

三、链表中倒数第K个结点

四、删除链表的倒数第n个结点 

五、环形链表

 六、环形链表Ⅱ

---

一、链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。 如果有两个中间结点，则返回第二个中间结点。

 先设置两个low和fast都指向head的结点。

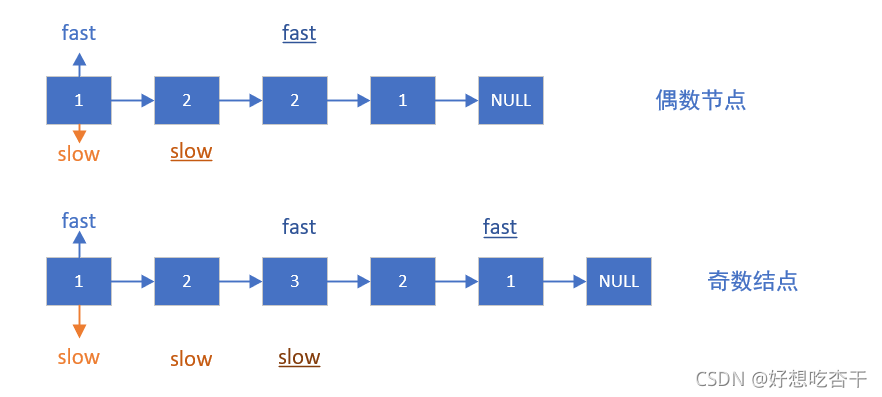
 现在是寻找中间结点，可以让fast一下子走两个结点，low走一个结点，两点同时向前进。

 当走到这儿的时候，会发现fast不能再继续走两步了，二low此时就是整个链表的中间结点。

这并不是一个巧合，此时就相同的时间t内，low的速度成为v，fast指针的速度为2v，low走了vt，fast走了2vt==链表长度，所以low走过的长为链表长度的一半，就是中间位置。所以整个循环的种植条件就是fast != null && fast.next != null，只要fast还能继续向后走，low就不是中间位置。

这种方法可以用来寻找链表的任意位置。

    public ListNode middleNode(ListNode head) {ListNode low = head;ListNode fast = head;while(fast != null && fast.next != null){fast = fast.next.next;low = low.next;}return low;}

二、回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

回文链表问题 = 反转链表 + 找到链表中间结点问题。

当我们已经找到中间结点mid时，把mid当做头结点，将剩下的链表反转称为l2，再与以head为头结点的链表遍历进行比较，所以这个时候循环的终止条件就是l2!=null。

 运用第一题中的方法能成功找到mid结点，然后成功反转后是这样的。

 这是就可以创建循环，然后head和l2的值相互比较，如果有一个不相同那么直接返回false，判断相同过后，head和l2继续向后移动，比较下一个。直到循环退出，则证明该链表是回文链表，返回true。

    public boolean isPalindrome(ListNode head) {ListNode mid = middleNode(head);ListNode l2 = reverseList(mid);while (l2 != null) {if (head.val != l2.val) {return false;}head = head.next;l2 = l2.next;}return true;}public ListNode middleNode(ListNode head) {ListNode low = head;ListNode fast = head;while(fast != null && fast.next != null){fast = fast.next.next;low = low.next;}return low;}public ListNode reverseList(ListNode head) {if (head == null || head.next == null) {return head;}ListNode prev = null;ListNode cur = head;while (cur != null) {ListNode next = cur.next;cur.next = prev;prev = cur;cur = next;}return prev;}

三、链表中倒数第K个结点

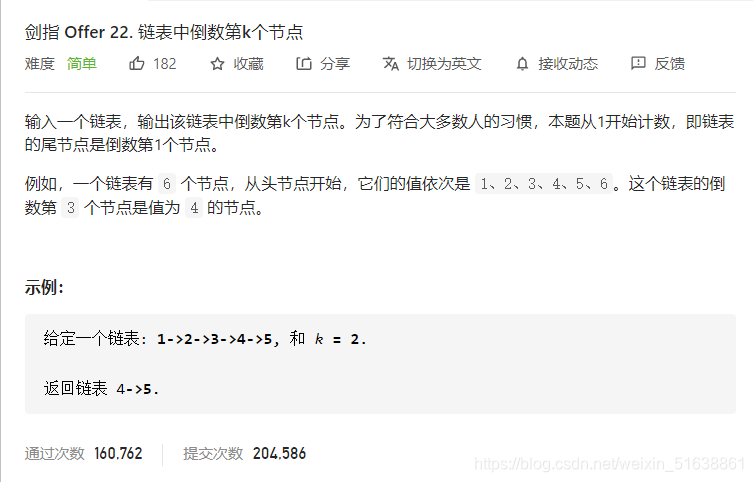
输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。

例如，一个链表有5个节点，从头节点开始，它们的值依次是1、2、3 、4、5，这个链表的倒数第2个节点是值为4的节点。

有了快慢指针的定义，我们可以先让sec走k步，然后prev和sec一起向前走，当sec为空了，prev当前的值就是倒数第k个结点了。

 刚开始时，prev和sec都在head的位置上，进入while循环中，当i<k时，只有sec可以向后移动。

当i==k时，sec已经比prev先走了k步，所以sec和prev都可以向后移动了。

 当sec走到最后时，sec==null，所以整个循环跳出，这就是循环的终止条件，这个时候的prev结点就是倒数第k个结点。

    public ListNode getKthFromEnd(ListNode head, int k) {ListNode prev = head;ListNode sec = head;int i = 0;while(sec!=null){if(i>=k){prev = prev.next;}i++;sec = sec.next;}return prev;}

四、删除链表的倒数第n个结点 

给定一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

这种情况就不能找到倒数第n个结点，要找到它的前驱结点。然后进行删除操作。所以这道题就是前驱结点+删除节点问题，所以我们需要自己创造一个前驱结点，node和prev都指向这个前驱结点，x也指向，最终由x来输出连链表。

 有了第三道题，这道题就很好解决了，这道题只需要让prev比node多走n+1步即可。

 当prev已经多走了n+1步时，node也可以开始走了，两者一起继续向前进直到prev==null。

 这时prev已经为空了，node就是倒数第n个结点的前驱结点，这时只需要让node.next = node.next.next，就成功删除需要删除的结点了。但是有个特殊情况那就是node.next还是head没有进入循环，这时如果直接将按照正常思路，那么还是不能删除第一个元素，所以需要排除这种情况直接让x.next = node.next.next，最后返回x。

public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode prev = new ListNode(-1);ListNode node = new ListNode(-1);ListNode x = new ListNode(-1);x.next = head;prev.next = head;node.next = head;int i = 0;while(prev!=null){if(i>n){node = node.next;}i++;prev = prev.next;}if(node.next == head){x.next = node.next.next;}else{node.next = node.next.next;}return x.next;}

五、环形链表

给你一个链表的头节点 head ，判断链表中是否有环。 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。 如果链表中存在环 ，则返回 true 。 否则，返回 false 。

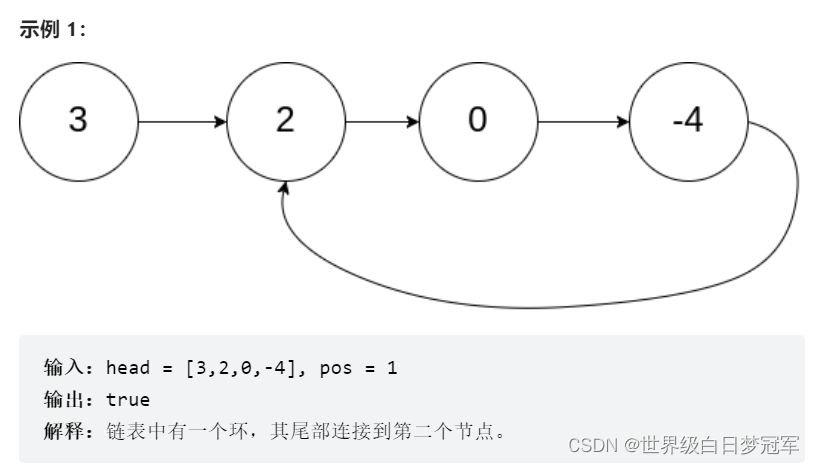
 这道题运用到了跑步比赛中的套圈知识，当你和同学一起跑步，他的速度是你的两倍，那么你和同学一定会在某一时刻相遇。

所以就设置一个node一个prev同时从头结点向后移动，prev每次走两个，node每次走一个。 

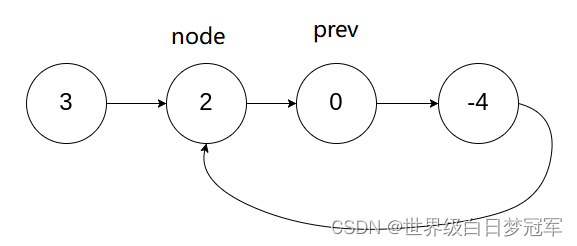
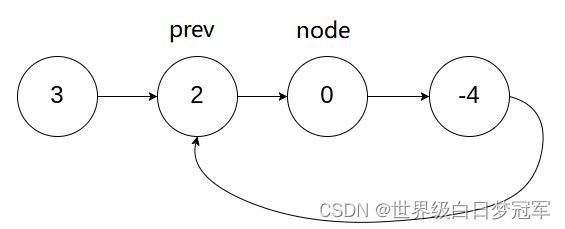
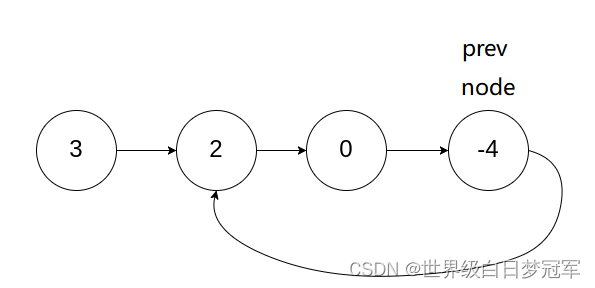
 移动过后会发现，node和prev真的会重合，所以这个时候这个链表就是有环的。在代码中这个快慢指针的追逐直到prev==null || prev.next==null时才会停止，这个时候链表是没有环的，prev首先到达了尾部。

    public boolean hasCycle(ListNode head) {if(head == null||head.next == null){return false;}ListNode node = head;ListNode prev = head;while(prev!=null&&prev.next!=null){node = node.next;prev = prev.next.next;if(prev==node){return true;}}return false;}

 六、环形链表Ⅱ

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。 不允许修改 链表。

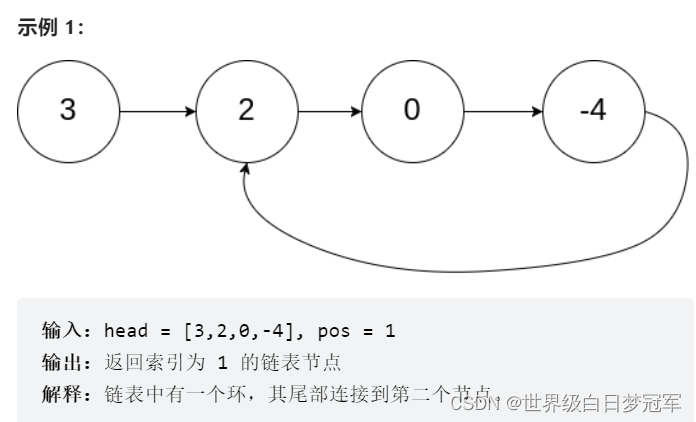
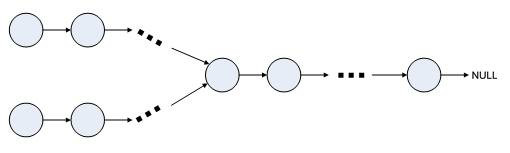
 第一个叉号是意味着环的入口，第二个叉号意味着用快慢指针相遇的结点，b就相当于慢指针在环内走的长度，c相当于环剩下的长度，a就是进环之前的长度。那么low走的长度是a+b。fast走了多少个环不确定就设置走了n个环，所以fast走的长度是a+b+n(b+c)。

low的速度为v，fast的速度为2v，在相同时间t时，fast走的长度是low的2倍，所以2(a+b) = a+b+n(b+c)，所以a = (n-1)(b+c)+c。所以当low和fast相遇后，设置一个third从头结点开始和low一起向后遍历，low再跑n-1圈后会一定会和third在环的入口相遇。

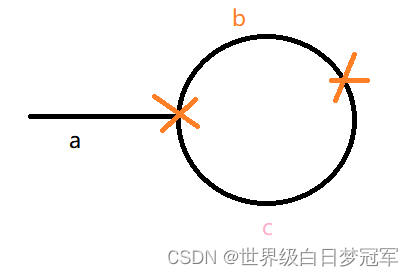
 结论：带环链表，快指针一次走两步，慢指针一次走一步，相遇之后，引入第三个指针从head开始向后遍历，则第三个指针一定会和慢指针在环的入口相遇。

 在第五题中得出low和fast相遇的点如图，如果此刻fast==null|| fast.next==null则证明链表没有环直接返回空即可。现在确定链表肯定有环了，创建third和low一起向后遍历，直到他俩相等。

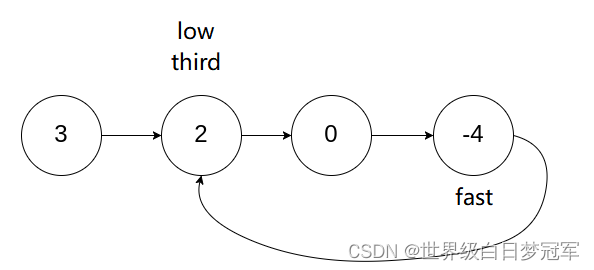
 如图在这种情况下只要再走一步third和low就相遇了，所以返回当前的third，就得到了环的入口。

    public ListNode detectCycle(ListNode head) {if(head==null||head.next==null){return null;}ListNode low = head;ListNode fast = head;ListNode third = head;while(fast.next!=null&&fast!=null){fast = fast.next.next;low = low.next;if(low==fast){break;}}if(fast==null|| fast.next==null){return null;}while(third!=low){third = third.next;low = low.next;}return third;}