快慢指针

快慢指针中的快慢指的是移动的步长，即每次向前移动速度的快慢。例如可以让快指针每次沿链表向前移动2，慢指针每次向前移动1次。

快慢指针的应用

（1）判断单链表是否存在环

如果链表存在环，就好像操场的跑道是一个环形一样。此时让快慢指针都从链表头开始遍历，快指针每次向前移动两个位置，慢指针每次向前移动一个位置；如果快指针到达NULL，说明链表以NULL为结尾，没有环。如果快指针追上慢指针，则表示有环。代码如下：

bool HasCircle(Node *head)
{if(head == NULL)return false;Node *slow = head, *fast = head;while(fast != NULL && fast->next!=NULL){slow = slow->next; //慢指针每次前进一步fast = fast->next->next;//快指针每次前进两步if(slow == fast) //相遇，存在环return true;}return false;
}

（2）在有序链表中寻找中位数

快指针的移动速度是慢指针移动速度的2倍，因此当快指针到达链表尾时，慢指针到达中点。

程序还要考虑链表结点个数的奇偶数因素，当快指针移动x次后到达表尾（1+2x），说明链表有奇数个结点，直接返回慢指针指向的数据即可。

如果快指针是倒数第二个结点，说明链表结点个数是偶数，这时可以根据“规则”返回上中位数或下中位数或（上中位数+下中位数）的一半。

while (fast && slow)
{if (fast->next==NULL)return slow ->data;else if (fast->next!= NULL && fast->next->next== NULL)return (slow ->data + slow ->next->data)/2;else{fast= fast->next;fast= fast->next;slow = slow ->next;}}

(3) 输出链表中的倒数第K个节点(即正数第K-1个节点)

可以定义两个指针，第一个指针从链表的头指针开始遍历向前走k-1步，第二个指针保持不动；从第K步开始，第二个指针也开始从链表的头指针开始遍历。由于两个指针的距离保持在k-1，当第一个指针到达链表的尾节点时候，第二个指针正好是倒数第K个节点，代码如下：

// 查找单链表中倒数第K个结点  
ListNode * RGetKthNode(ListNode * pHead, unsigned int k) // 函数名前面的R代表反向  
{  if(k == 0 || pHead == NULL) // 这里k的计数是从1开始的，若k为0或链表为空返回NULL  return NULL;  ListNode * pAhead = pHead;  ListNode * pBehind = pHead;  for(int i=0;i<k-1;i++){  pAhead=pAhead->next;  if(pAhead==null)  return null;//当链表长度小于k时候，返回Null  }  while(pAhead->next != NULL)  // 前后两个指针一起向前走，直到前面的指针指向最后一个结点  {  pBehind = pBehind->next;  pAhead = pAhead->next;  }  return pBehind;  // 后面的指针所指结点就是倒数第k个结点  
}

(4) 判断链表是否存在环，如果存在，找到环入口

有一个单链表，其中可能有一个环，也就是某个节点的next指向的是链表中在它之前的节点，这样在链表的尾部形成一环。

如何判断一个链表是否存在环？设定两个指针slow，fast，均从头指针开始，每次分别前进1步、2步。如存在环，则两者相遇；如不存在环，fast遇到NULL退出。

如果链表存在环，如果找到环的入口点？当fast若与slow相遇时，slow肯定没有走遍历完链表或者恰好遍历一圈。于是我们从链表头与相遇点分别设一个指针，每次各走一步，两个指针必定相遇，且相遇第一点为环入口点。

node* findLoopPort(node *head) {node *fast, *slow;fast = slow = head;while (fast && fast->next) {  
//第一步：判断链表是否存在环slow = slow->next;fast = fast->next->next;if (slow == fast) { //链表存在环break;}}if ((fast == NULL) || (fast->next == NULL)) {  //链表不存在环return NULL;}
//第二步：寻找环的入口点slow = head; //让slow回到链表的起点，fast留在相遇点while (slow != fast) { //当slow和fast再次相遇时，那个点就是环的入口点slow = slow->next;fast = fast->next;}return slow;
}

(5) 判断两个单链表是否相交，如果相交，找到他们的第一个公共节点

判断两个单链表是否相交,如果相交，给出相交的第一个点（假设两个链表都不存在环）。

思路：

首先利用快慢指针判断链表是否存在环。

(1)如果都不存在环，则如果两个单向链表有公共节点，也就是两个链表从某一节点开始，他们的p_next都指向同一个节点，每个节点只有一个p->next。因此从第一个公共节点开始，之后它们所有节点都是重合的。因此，首先两个链表各遍历一次，求出两个链表的长度L1、L2，然后可以得到它们的长度差L。然后现在长的链表上遍历L个节点，之后再同步遍历，于是在遍历中，第一个相同的节点就是第一个公共的节点。此时，若两个链表长度分别为M，N,则时间复杂度为O(M+N).

(2)如果一个存在环，另外一个不存在环，则这两个链表是不可能相交的。

(3)如果利用快慢指针发现两个链表都存在环，则判断任意一个链表上快慢指针相遇的那个节点，在不在另外一个链表上，如果在，则相交，不在，则不相交。

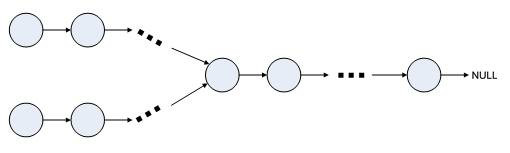
下面讨论两个没有环的链表如果是相交于某一结点的情况：

相交的链表示意图如下所示：

这里写图片描述

方法一：

两个没有环的链表如果是相交于某一结点，如上图所示，这个结点后面都是共有的。所以如果两个链表相交，那么两个链表的尾结点的地址也是一样的。程序实现时分别遍历两个单链表，直到尾结点。判断尾结点地址是否相等即可。时间复杂度为O(L1+L2)。

如何找到第一个相交结点？判断是否相交的时候，记录下两个链表的长度，算出长度差len，接着先让较长的链表遍历len个长度，然后两个链表同时遍历，判断是否相等，如果相等，就是第一个相交的结点。

void Is_2List_Intersect(LinkList L1, LinkList L2) {if (L1 == NULL || L2 == NULL) {exit(ERROR);}LinkList p = L1;LinkList q = L2;int L1_length = 0;int L2_length = 0;int len = 0;while (p->next) {L1_length ++;p = p->next;}while (q->next) {L2_length ++;q = q->next;}printf("p: = %d\n", p);printf("q: = %d\n", q);printf("L1_length: = %d\n", L1_length);printf("L2_length: = %d\n", L2_length);if (p == q) {printf(" 相交\n");/*p重新指向短的链表 q指向长链表*/if (L1_length > L2_length) {len = L1_length - L2_length;p = L2;q = L1;}else {len = L2_length - L1_length;p = L1;q = L2;}while (len) {q = q->next;len--;}while (p != q) {p = p->next;q = q->next;}printf("相交的第一个结点是：%d\n", p->data );}else {printf("不相交 \n");}}

方法二：

另外一个方法则是将一个链表首尾相接，然后判断另外一个链表是否有环，如果有环，则两个链表相交。那么求第一个交点则求出有环的的那个链表的环结点即是。

int Is_ListLoop(LinkList L) {LinkList fast, slow;if (L == NULL || L->next == NULL) {exit(ERROR);}fast = slow = L;while (fast->next != NULL && fast->next->next != NULL) {slow = slow->next;fast = fast->next->next;if (fast == slow) {return True;}}return False;
}int Find_Loop(LinkList L) {LinkList fast, slow;if (L == NULL || L->next == NULL) {exit(ERROR);}fast = slow = L;while (fast->next != NULL && fast->next->next != NULL) {slow = slow->next;fast = fast->next->next;if (fast == slow) {break;}}slow = L;while (fast != slow) {slow = slow->next;fast = fast->next;}printf("%d\n", slow->data );return TRUE;}void Is_2List_Intersect2(LinkList L1, LinkList L2) {if (L1 == NULL || L2 == NULL) {exit(ERROR);}LinkList p = L1;LinkList q = L2;while (p->next) {p = p->next;}p->next = L1->next;if(Is_ListLoop(L2)){printf("相交\n");printf("相交的第一个结点是：");Find_Loop(L2);}else{printf("不相交\n");}
}

参考链接：

https://blog.csdn.net/a1091220321/article/details/47706711

https://www.cnblogs.com/hxsyl/p/4395794.html

https://blog.csdn.net/zwhlxl/article/details/45745825