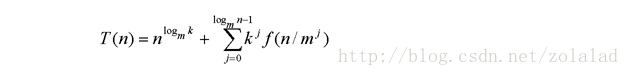算法:求解具体问题的步骤描述,代码上表现出来是解决特定问题的一组有限的指令序列。
1、分治:
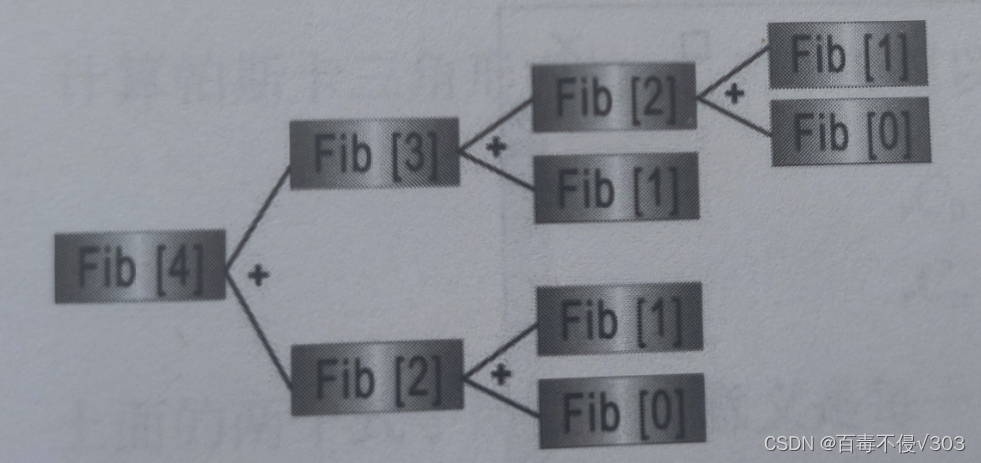
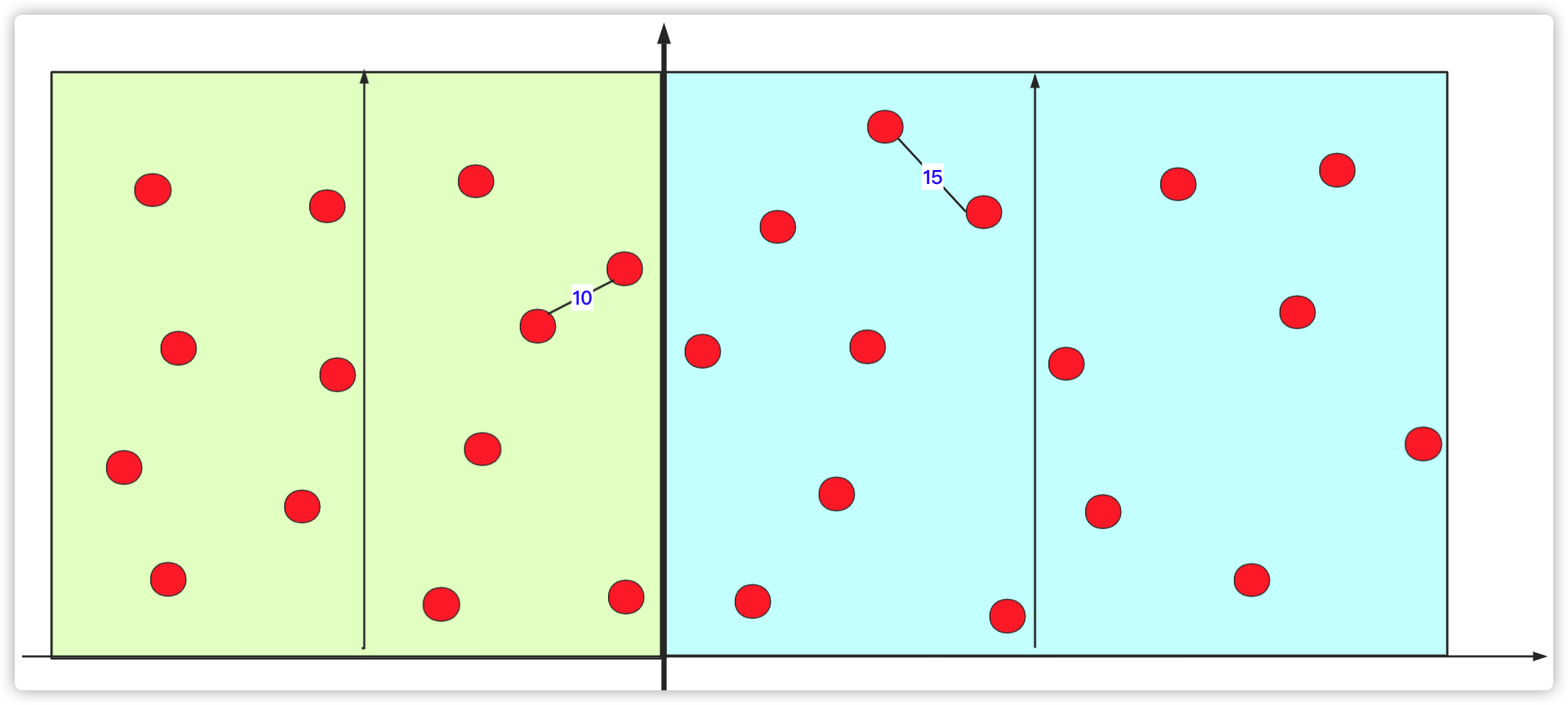
算法思想:规模为n的原问题的解无法直接求出,进行问题规模缩减,划分子问题(这里子问题相互独立而且和原问题解的性质是相同的,只是问题规模缩小了)。如果子问题的规模仍然不够小,再进行子问题划分,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止,最后将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原问题的解。
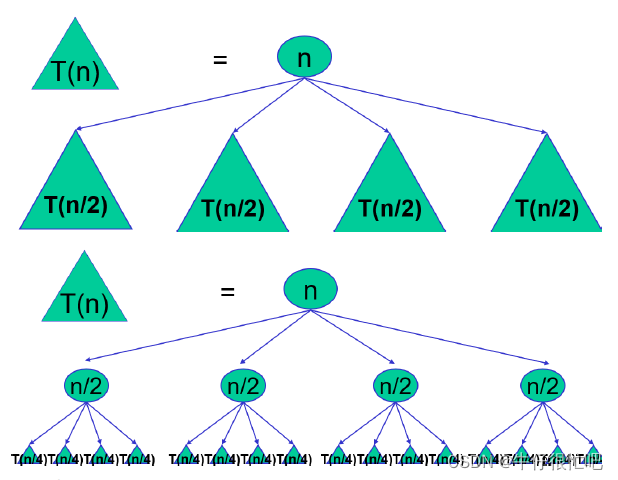
分治算法适用条件:
分治法所能解决的问题一般具有以下几个特征:
1.原问题的规模缩小到一定的程度就可以容易地解决
2.原问题可以分解为若干个规模较小的相同问题,即原问题具有最优子结构性质
3.利用原问题分解出的子问题的解可以合并为原问题的解
4.原问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题(这条特征涉及到分治法的效率,如果各个子问题不独立,也就是子问题划分有重合的部分,则分治法要重复的求解公共子问题的解,此时虽然也可用分治法,但采用动态规划更好)。
2、动态规划:
算法思想:算法的基本思想与分治算法类似,也是将待求解的问题划分为若干子问题,按划分的顺序求解子阶段问题,前一个子问题的解,为后一子问题的求解提供了有用的信息(最优子结构)。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其它局部解。依次解决各个子问题,最后求出原问题的最优解。
与分治算法最大的区别是:适合于用动态规划算法求解的问题,经分解后得到的子问题往往不是互相独立的。

动态规划求解问题的基本步骤:
动态规划所处理的问题是一个多阶段决策问题,一般由初始状态开始,通过对中间阶段决策的选择,达到结束状态。动态规划算法的代码设计都有一定的模式,一般都要经过以下几个步骤:
初始状态 -> 决策1 -> 决策2 -> ... -> 决策n -> 结束状态
1.找出最优解的性质,并刻划其结构特征。(找问题状态)
2.递归地定义最优值。(找状态转移方程)
3.自底向上的方式计算出最优值。
4.根据计算最优值时得到的信息,构造最优解。
3、贪心:
当一个问题具有最优子结构性质时,可以使用动态规划法求解,但有时候使用贪心算法更简单,更直接而且解决问题的效率很高。例如前面动态规划算法中的硬币问题就可以用贪心算法来解决,从算法名字上来看,贪心算法总是做出在当前看来最好的选择,也就是说贪心算法并不从整体最优考虑,它所做出的选择只是在某种意义上的局部最优选择,当然最终希望贪心算法得到的最终结果也是最优的。
虽然贪心算法不能对所有问题都得到整体最优解,但是对于很多问题它能够产生整体最优解,或者是趋近于最优解。
4、回溯法(暴力求解+剪枝操作):
算法思想:在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根节点出发深度搜索解空间树。当搜索到某一节点时,要先判断该节点是否包含问题的解,如果包含就从该节点出发继续深度搜索下去,否则逐层向上回溯。一般在搜索的过程中都会添加相应的剪枝函数,避免无效解的搜索,提高算法效率。
解空间:解空间就是所有解的可能取值构成的空间,一个解往往包含了得到这个解的每一步,往往就是对应解空间树中一条从根节点到叶子节点的路径。子集树和排列树都是一种解空间,它们不是真实存在的数据结构,也就是说并不是真的有这样一颗树,只是抽象出的解空间树。
子集树模板代码:
void func(int *arr,int i,int length,vector<int>& x)
{if(i == length) //递归结束的条件{for(int v : x){cout << v << " ";}cout << endl;}else{x.push_back(arr[i]); //选择i节点func(arr,i+1,length,x); //遍历i的左孩子x.pop_back(); //不选择i节点func(arr,i+1,length,x); //遍历i的右孩子}
}int main()
{int arr[] = {1,2,3};int length = sizeof (arr) / sizeof (arr[0]);vector<int> x; //辅助数组,记录节点的状态,向左递归还是向右递归func(arr,0,length,x);return 0;
}排列树:
void func(int arr[],int i,int length)
{if(i == length){for(int j = 0;j < length;++j){cout << arr[j] << " ";}cout << endl;}else{//生成i节点的所有孩子节点for(int k = i;k < length;++k){swap(arr[i],arr[k]);func(arr,i+1,length);swap(arr[i],arr[k]); //交换回来}}
}
int main()
{int arr[] = {1,2,3,4};int length = sizeof(arr)/sizeof(arr[0]);func(arr,0,length);
}
5、分支限界:
分支限界法类似于回溯算法,是在问题的解空间树上搜索问题解的算法,主要体现在两点不同:
1.求解目标不同。回溯算法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标是找出满足约束条件的一个解,或者是在满足约束条件的解中找出某种意义下的最优解。
2.搜索解空间树的方式不同。回溯算法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或者以最小耗费优先的方式搜索解空间树。
分支限界算法基本思想:
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。在分支限界法中,每一个活结点只有一次机会称为扩展节点,活结点一旦成为扩展节点,就一次性产生其所有儿子节点(分支),在这些儿子节点中,导致不可行解或是导致非最优解的儿子节点会被舍弃掉,其余儿子节点会被加入活结点表中。
为了有效的选择下一个扩展节点加速搜索,在每一个活结点处计算一个函数值(限界),并根据计算的函数值结果从当前活结点表中取下一个最有利的节点成为当前的扩展节点,使搜索朝着解空间树上最优解的分支推进。重复上述节点扩展过程,直到找到所需的最优解或者活结点表为空。