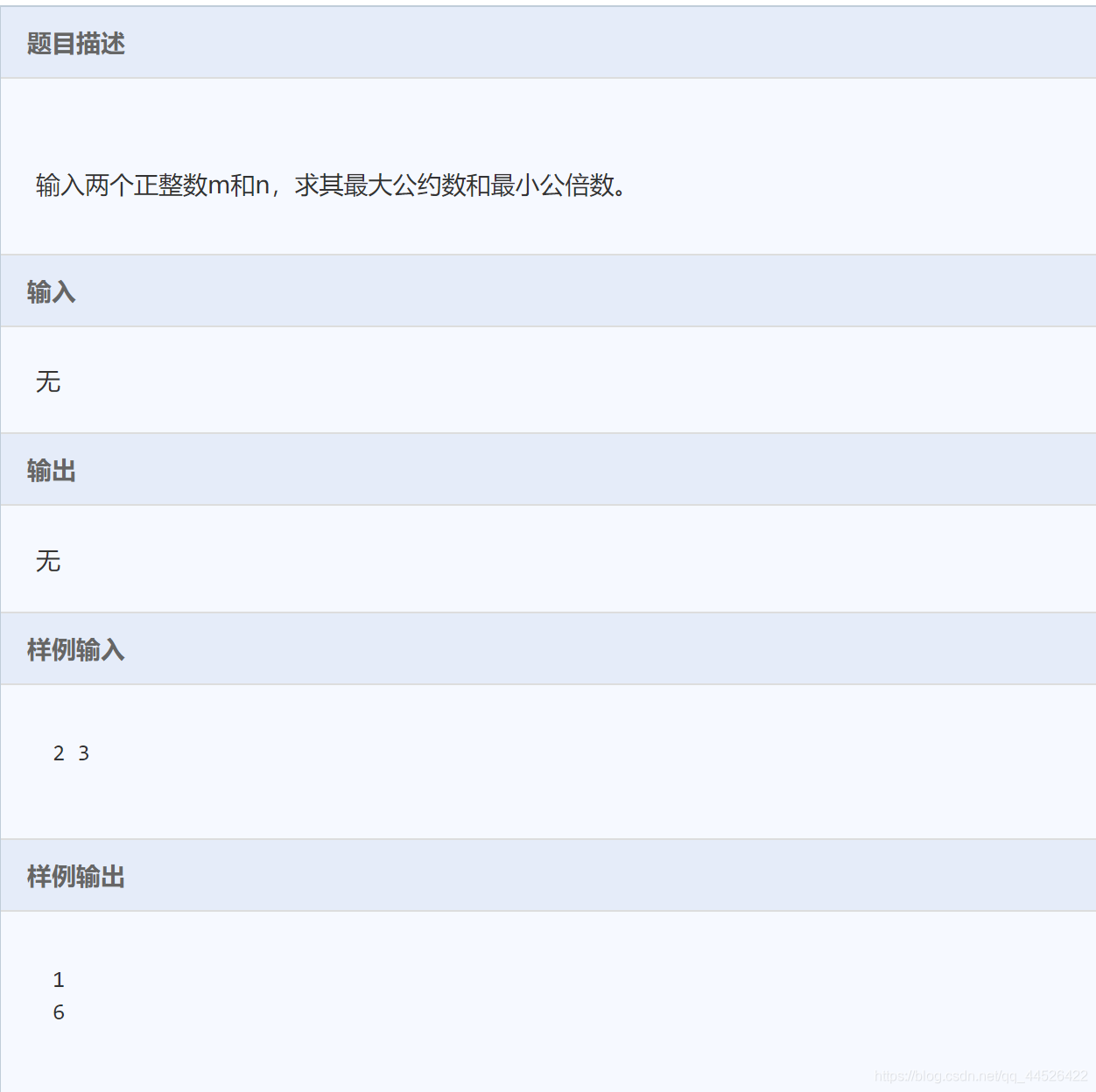
一、求最大公因数的三种方法:
最大公因数定义:
(最大公约数、最大公因子):指两个或多个整数共有约数中最大的一个。

最小公倍数定义:
两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。
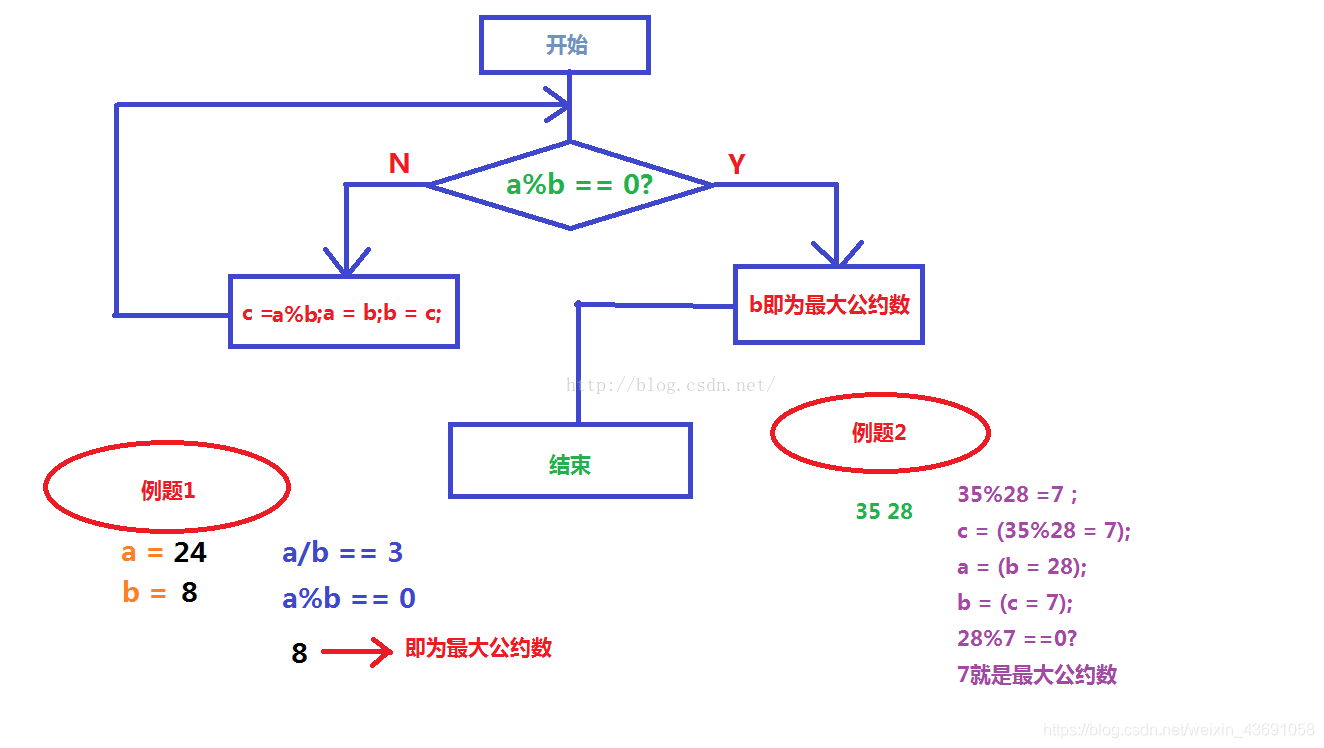
①辗转相除法(欧几里得算法):
用较大数除以较小数,再用除数继续除以余数求出新的余数,不停循环直到余数等于0,此时除数就是最大公约数。
int gcd(int a, int b)
{return a % b == 0 ? b : gcd(b, a%b);
}
int gcd(int x,int y)
{int z=y;while(x%y!=0){z=x%y;x=y;y=z; }return z;
}
c÷b,读作c除以b(或b除c)。其中,c叫做被除数,b叫做除数,
②更相减损术:
用较大数减去较小数,再不断用差减减数得到新的差(当差是负数时,就反过来减),不停循环直到减数和差相等为止,此时这个相等的数就是最大公约数。

int gcd(int a,int b)
{while(a!=b){if(a>b){a=a-b;}else{b=b-a;}}return a;
}
③穷举法:
从其中一个数字开始,依次递减,直到某个数除以两个数的余数都是0,此时这个数就是最大公约数。
int gcd(int x,int y)
{int t;for(t=x;;t--){if(x%t==0 && y%t==0)break;}return 0;
}二、求最小公倍数:
①公式:lcm=x*y/gcd
求两个数x和y的最小公倍数时, 最小公倍数=x*y/最大公约数。
②穷举法
int lcm(int x,int y)
{if(x*y==0)return 0;int max = a > b ? a : b ;while(1){if(max%a==0 && max%b==0)break;max--;}return max;
}
部分内容借鉴博客:https://blog.csdn.net/chen_zan_yu_/article/details/82943306