相关文章
线性代数学习之正交性,标准正交矩阵和投影
正交基和标准正交基:
前言:
经过上一次线性代数学习之向量空间,维度,和四大子空间的学习,对于空间的概念已经有了非常深刻的认识了,而描述空间很重要的方式除了维度以外,那就是空间的基了&…
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(8):标准正交基与Gram-Schmidt过程
目录 前言往期文章2.2 标准正交基与Gram-Schmidt过程2.2.1 标准正交基定义2.4定理2.2.1定义2.5 2.2.2 求标准正交基的Schmide方法定理2.2.2举例 结语 前言 Hello!小伙伴! 非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指…
c语言实现向量组的标准/规范正交基(施密特正交化)
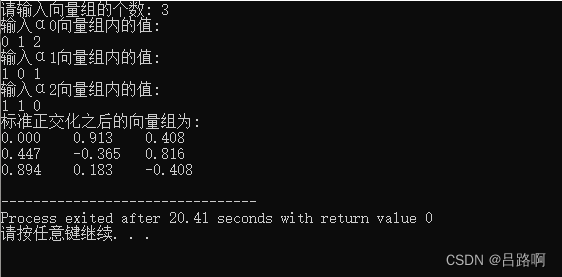
问题:任意一个向量组求标准正交基,尽量用C/C。
思路:下面是我找的课本上面的算向量组标准正交基的方法。第一步,用施密特正交化方法,使向量组正交;第二步,将向量组各向量单位化。
代码实现&a…
线性代数(三十九) :格拉姆-施密特正交化与标准正交基
本节介绍正交的概念,以及将基变为正交基的格拉姆-施密特(Gram-Schmidt)方法
1 正交
如果向量x,y满足: 则称x与y正交(orthogonal)或者垂直(perpendicular),记做: 2 标准正交基
设X是具有欧几里得结构的有限维线性空间 是X的一组基,如果他们满足&#x…
线性代数(14)——正交性、标准正交基和投影
正交性、标准正交基和投影 正交基与标准正交基一维投影高维投影和Gram-Schmidt过程三维空间四维及以上空间实现Gram-Schmidt过程相关话题 标准正交基的性质 正交基与标准正交基
一个 n n n维空间中任何一组线性无关的向量,都是这个 n n n维空间的一组基。当这组基的…
线性代数中一组基向量的标准正交化原理通熟易懂理解
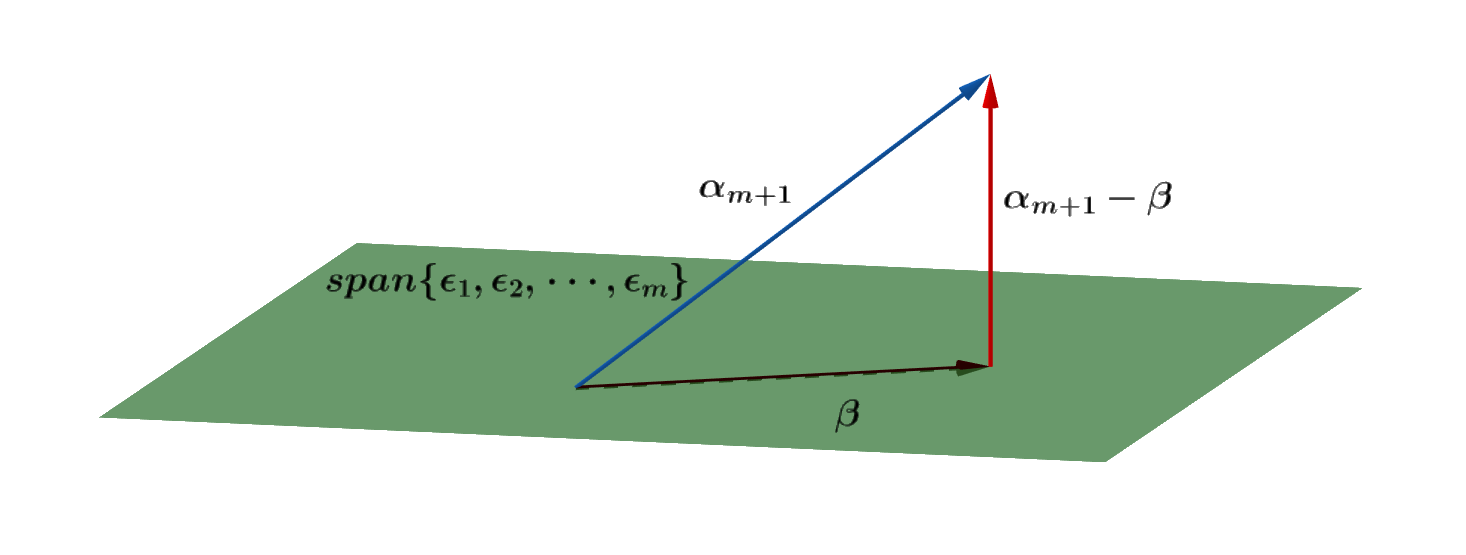
我们先来看图,看看这个方法的操作过程,等一下,我找找我的大学的线性代数课本,找到啦!(哈哈,虽然读研了,因为我是菜鸟,所以还是随时带着)如下图所示࿱…
【机器学习】【线性代数】正交基、标准正交基、正交矩阵,正交变换等数学知识点
1.正交向量组
直接给定义:欧式空间V的一组非零向量,如果他们俩俩向量正交,则称是一个正交向量组。
(1)正交向量组 是 线性无关的
(2)n维欧式空间中俩俩正交的非零向量不会超过n个,…
为什么总是标准正交基(标准直角坐标系)?
坐标系的作用是什么?简单的一句换就是,坐标系是拿来描述点的位置的。要对事物进行分析,无论是量化分析还是抽象分析,需要首先对事物有一个清晰的定义,这样我们才能知道我们在说什么。对事物进行定义时,特别…
空间的基,自然基,标准正交基
误区:总以为二维平面的基是垂直的x轴和y轴 总以为三维空间的基是垂直的x轴,y轴和z轴
解析:
以二维空间为例,不光只有垂直的两个向量才能表示整个空间。 如上图所示,垂直的两个向量能表示整个平面自不必多说。
下图…
标准正交基(Orthonormal)、施密特正交化(Gram-Schmidt)
标准正交基、施密特正交化 1.标准正交基(Orthonormal)与施密特正交化(Gram-Schmidt)1.1 标准正交基(Orthonormal)1.2 施密特正交化(Gram-Schmidt) 1.标准正交基(Orthonor…
后端的setCookie无法写入浏览器的问题
知识点:
后端通常称为session,是tomacat自带的验证方式,前端叫cookies的存储存这个cookies,有时效性,通常是后台设置(前端也可以设置,一般不)。也就是说业务上,如果使用…
EditThisCookie使用
下载安装
http://www.cnplugins.com/uploads/plugins/201502/www.cnplugins.com_fngmhnnpilhplaeedifhccceomclgfbg_1_4_1_.crx从上面这个网址下载下来,下下来之后用Chrome插件伴侣制作成谷歌浏览器能直接添加的插件
使用
鼠标右键单击——>EditThisCookie&am…
HttpCookie
下面我们讲HttpCookie的用法: 什么是Cookie?: cookie是存储于访问者的计算机中的变量。每当同一台计算机通过浏览器请求某个页面时,就会发送这个cookie。你可以使用 JavaScript 来创建和取回cookie的值。 Cookie的用途࿱…
setcookie()函数
https://www.cnblogs.com/yuanwanli/p/5808472.html
欢迎使用Markdown编辑器
你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。
新的改变
我们对…
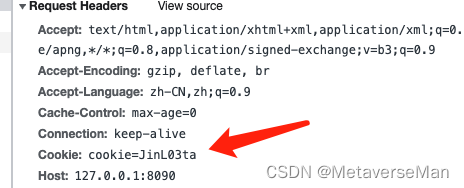
解决Gin框架下 浏览器(chrome)在setcookie()后不能成功携带cookie的问题
参考gin官网的文档给出的代码:地址在https://gin-gonic.com/zh-cn/docs/examples/cookie/
func CookieMiddleWare() gin.HandlerFunc {return func(c *gin.Context) {cookieValue, err : c.Cookie("cookie")if err ! nil {//c.AbortWithStatusJSON(403, …