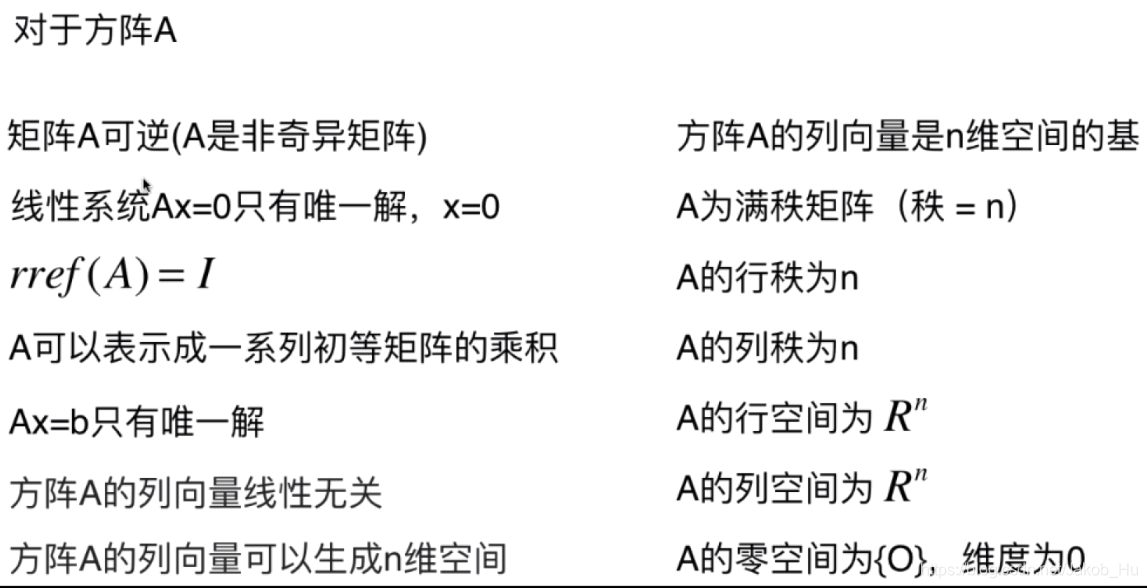
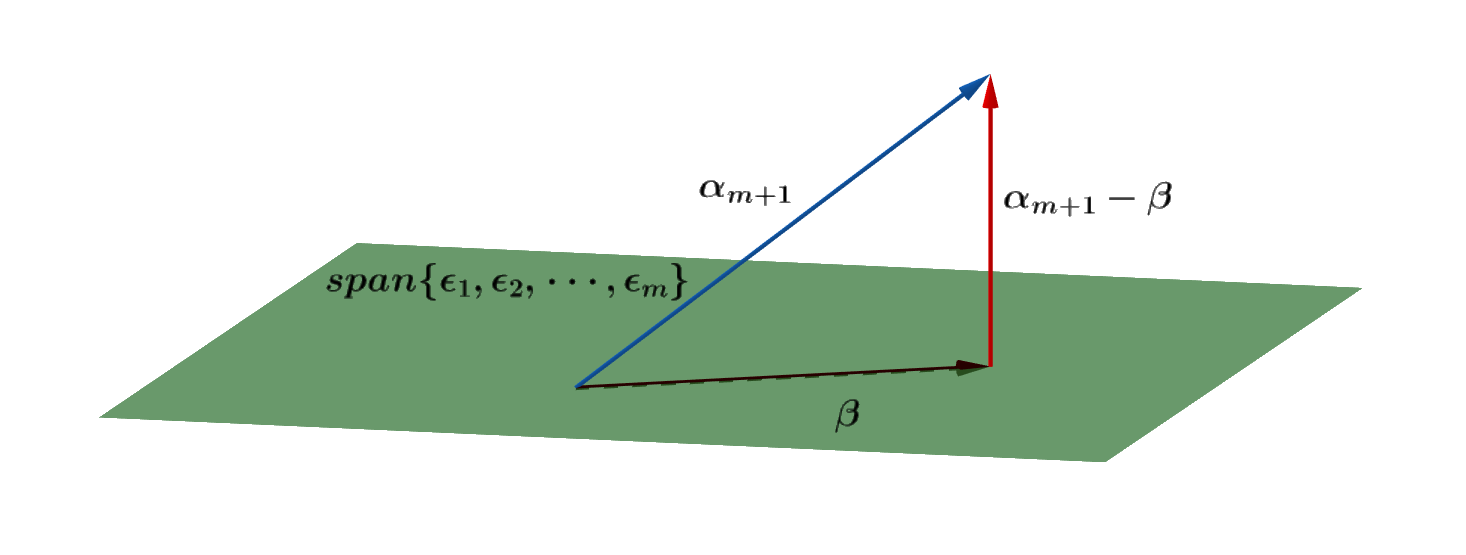
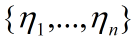问题:任意一个向量组求标准正交基,尽量用C/C++。
思路:下面是我找的课本上面的算向量组标准正交基的方法。第一步,用施密特正交化方法,使向量组正交;第二步,将向量组各向量单位化。

代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<math.h>int main(void)
{int dim, i, j, k;bool judge;//输入向量组的值,并存入二维数组中 printf("请输入向量组的个数: ");scanf("%d", &dim);double matrix[dim][dim];double replica[dim][dim];for(i=0;i<dim;i++){printf("输入α%d向量组内的值:\n",i); for(j=0;j<dim;j++)scanf("%lf", *(matrix+i)+j);}//由于输入问题,将各向量组转置 for(i=0;i<dim;i++)for(j=0;j<dim;j++)*(*(replica+i)+j) = *(*(matrix+i)+j);for(i=0;i<dim;i++)for(j=0;j<dim;j++)*(*(matrix+i)+j) = *(*(replica+j)+i); //施密特正交化,将向量组正交double a, b;double proj_vector[dim];for(i=1;i<dim;i++){for(k=0;k<dim;k++)proj_vector[k] = 0;for(j=0;j<i;j++){a = b = 0;for(k=0;k<dim;k++){a += matrix[k][i] * matrix[k][j];//计算两个向量的积,做分子b += matrix[k][j] * matrix[k][j];//计算向量与自身的内积,做分母 }for(k=0;k<dim;k++)proj_vector[k] += a / b * matrix[k][j];}for(k=0;k<dim;k++)matrix[k][i] = matrix[k][i] - proj_vector[k];}//单位化 for(i=0;i<dim;i++){b = 0;for(j=0;j<dim;j++)b += matrix[j][i] * matrix[j][i];for(j=0;j<dim;j++)matrix[j][i] = matrix[j][i] / sqrt(b);}//输出标准正交化后的值 printf("标准正交化之后的向量组为:\n");for(i=0;i<dim;i++){for(j=0;j<dim;j++)printf("%-9.3f",matrix[i][j]);putchar('\n');}return 0;
}
结果展示:
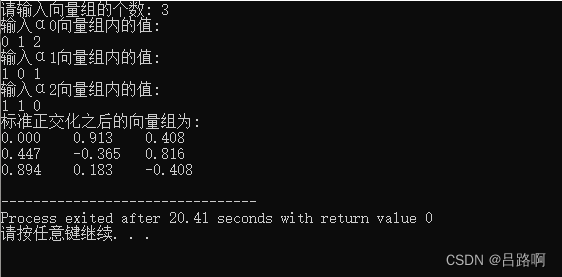
参考:https://blog.csdn.net/Nolan__Roronoa/article/details/52292041?app_version=5.8.1&code=app_1562916241&csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%2252292041%22%2C%22source%22%3A%22qq_44749483%22%7D&uLinkId=usr1mkqgl919blen&utm_source=app