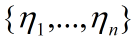定义

• 施密特正交化（Schmidt orthogonalization）是求欧氏空间正交基的一种方法。从欧氏空间任意线性无关的向量组α1，α2，……，αm出发，求得正交向量组β1，β2，……，βm，使由α1，α2，……，αm与向量组β1，β2，……，βm等价，再将正交向量组中每个向量经过单位化，就得到一个标准正交向量组，这种方法称为施密特正交化。

为什么正交化

• 在一个平面，或者三维空间中，任意一点都可以被坐标系表示出来。而我们更喜欢的是单位直角坐标系，因为在一个单位直角坐标系中，任意一个向量的坐标分量，通过简单的投影就可以搞定。
• 因此，如何找到欧式空间的一个“直角坐标系”，变得非常重要。施密特正交化法就告诉我们了一种把“任意坐标系”变为“直角坐标系”的方法。

意义

• 把一个普通矩阵转换成正交矩阵

正交矩阵

• 正交矩阵的转置就是正交矩阵的逆

α₂ 在α₁ 的投影向量

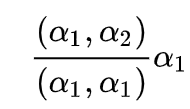
• 黄线部分即其投影

二维空间

• 要记得进行单位化

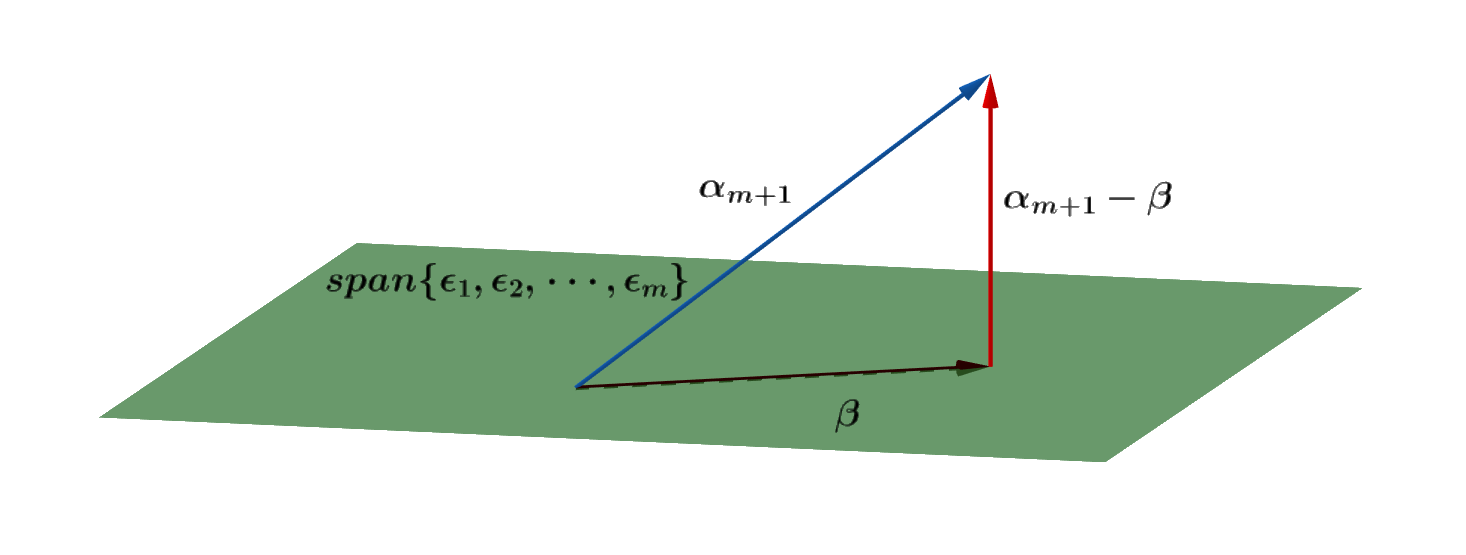
理解施密特正交化

• 以两个线性无关的向量α1​和α2​（红色）为例说明如何实现正交化。令β1=α1​，观察图片不难发现，蓝色虚线所代表的向量所要求的β2​(因为它和β1​垂直)，而这个蓝色的向量刚好可由α2​减去β1​

通式

标准正交基

• 若一组正交基内的基向量的模长都是单位长度1，则称这组正交基为标准正交基或规范正交基
  

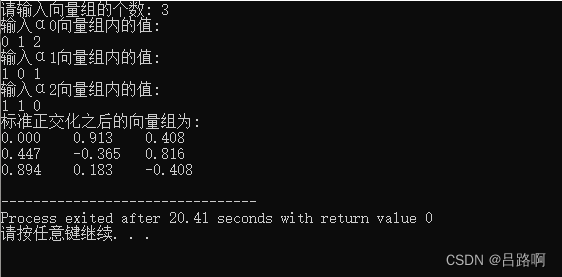
例题

不唯一

• 正交化的向量组不唯一. 按施密特正交化过程, 我们将向量组中的向量打乱顺序得到的向量组也不一样，标准正交基也不是唯一的.