为什么总是标准正交基（标准直角坐标系）？

article/2025/9/29 2:25:56

坐标系的作用是什么？简单的一句换就是，坐标系是拿来描述点的位置的。要对事物进行分析，无论是量化分析还是抽象分析，需要首先对事物有一个清晰的定义，这样我们才能知道我们在说什么。对事物进行定义时，特别在涉及到点的位置描述时，我们往往就需要借坐标系，这样我们可以简单方便的对点的位置有一个清晰的描述。

对点的描述是通过坐标给出，但是单纯的一个坐标没有任何意义，因为坐标只是一个有序对，其中的数字代表什么含义呢？只有当我们明确了基，我们才知道这个坐标在表达什么。甚至如果我们想知道某个坐标对应的绝对位置时，我们还需要明确原点的位置。所以，一个坐标系统两个要素就是：基和原点。如果我们知道了基，我们就知道两个点的相对位置，如果我们还知道原点，我们就还知道点的绝对位置。

当对现实世界中的事物进行分析建模时，并且需要进行现实应用时，我们往往需要同时明确一个坐标系统的基和原点，因为我们需要知道现实世界中事物的绝对位置。当对非现实世界的事物进行抽象分析，我们往往只在乎点的相对位置，因此这时候原点的位置便不再重要，此时我们只需要随意定义一个原点位置即可。

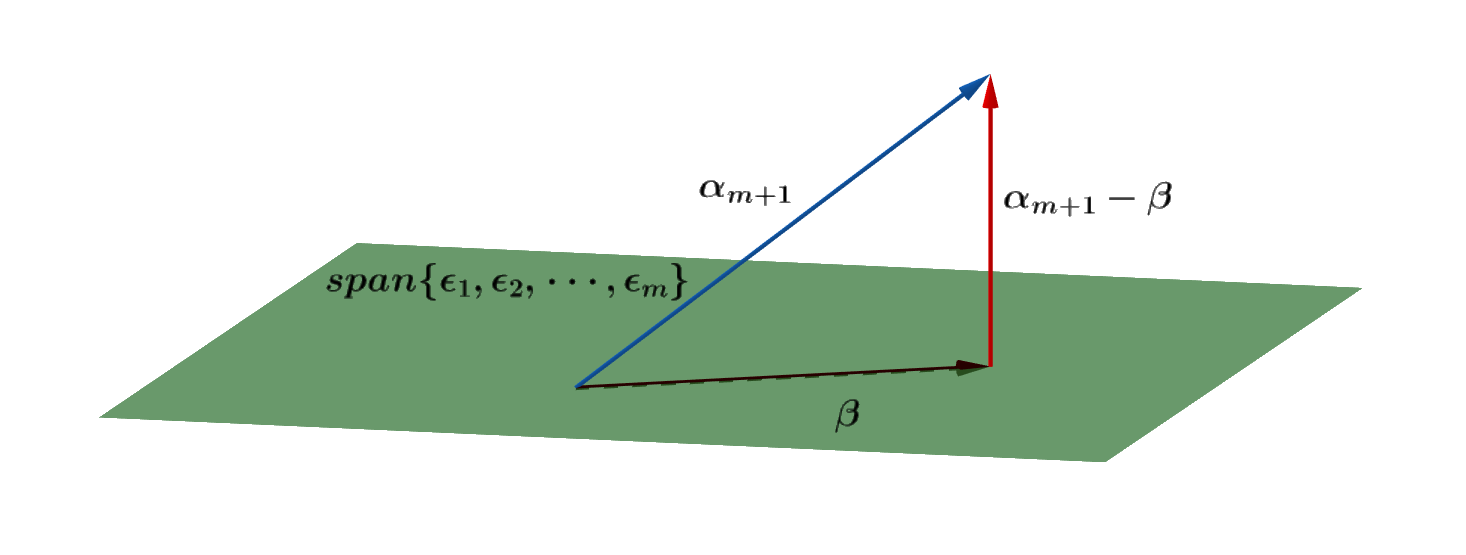
上面说过，一个坐标系统的两大要素是基和原点，原点我们已经说过了，剩下的还有基。我们定义一个坐标系统时，除了原点，还需要定义一组基，基是线性无关的，即无法相互线性表达，基的个数表示该坐标系统可以表达的空间维度。比如我们要表达一个二维平面上的点，那么基就是两个，表达三维空间的点，基就是三个，以此类推。但是对于一个n维的空间，有无数组基可以表达，只要这组基满足有k个且互不线性相关即可。

既然一个空间上的点，有无数组基可以表达，那么为什么我们经常看到的都是标准正交基呢？对应的就是标准直角坐标系。为什么不是别的基，比如对于一个二维平面，为什么不是用夹角60度的两个基，而是互相垂直的两个基？事实上，对于某个问题，我们可以用无数组基来进行表达，然后分析，我们选定某组基的理由是这样选取，会方便简化我们的分析。因此，我们对于基的选取，不是因为只有这样选才能分析出结论，而是这样选取会简化我们分析而已，不同的基本质等价的。因此，对于不同的问题，我们并不总是选取标准正交基，选取什么样的基，取决于什么样的基可以更见的简化和方便我们的分析。

因此，我们要回答为什么总是标准正交基这个问题，实际上就是要回答，什么情况下，标准正交基可以更加的简化我们的分析。首先，为什么总是标准化的基，这个问题很简单，因为标准化后的单位基可以让不同维度的坐标表示相同的尺度。我们分析问题时，往往不会刻意的区分不同维度上坐标的尺度，即我们不区分不同维度的特征，这样，不同维度上相同的坐标代表相同的尺度。除非特殊问题，不然我们不会给不同维度的基赋予不同尺度，这是在自己增加额外信息，自找麻烦。所以，为了更加的简化分析，我们往往赋予不同维度的基相同的尺度，因此直接对基进行标准化就可以达到这个目的，这也是为什么我们总是选取标准基的原因。

标准基的问题已经解答了，接下来的问题是，什么样的情况下，同时选取正交基是更有助于简化分析的。答案就是，当我们的分析涉及到向量的距离长度和角度时，这时选取正交基是可以简化距离长度和角度的表达的。

要定义长度，首先要定义内积。这里要注意的是，不能想当然的认为某个坐标，即某个向量的长度就是坐标的平方和开根号，这种计算长度的方式是在标准正交基和点积定义的基础上的。内积是线性空间中的一种操作，只需要满足几个条件即可，所以内积也可以有无数种具体的定义。但是需要合理的定义长度和角度时，就需要引入点积。点积是内积的一种，点积可以对我们直观的距离长度和角度有一个准确的定义。这里合理的定义长度和距离中的“合理”的意思是，可以准确描述表达我们现实三维空间中的距离和角度，因此，定义了点积的线性空间，就是我们所说的欧式空间。两个向量点积的定义如下所示：

$a\cdot b=|a||b|cos\theta$

其中的|a|表示向量a的模，即长度， $\theta$ 为向量a和b的夹角。根据此定义，只要我们定义了基的长度和夹角，那么所有向量的点积都可以计算出来。例如，向量a=(x1,y1)，b=(x2,y2)，基为e1,e2，其为标准基，即基的模为1，基的夹角为 $\beta$ ，则向量a和b的点积如下：
$a\cdot b=(x_{1}e_{1}+y_{1}e_{2})(x_{2}e_{1}+y_{2}e_{2})=x_{1}x_{2}e_{1}e_{1}+y_{1}y_{2}e_{2}e_{2}+(x_{1}y_{2}+x_{2}y_{1})e_{1}e_{2}=x_{1}x_{2}+y_{1}y_{2}+(x_{1}y_{2}+x_{2}y_{1})cos\beta$

根据点积定义，我们就可以定义任何向量a的长度为：

$|a|=\sqrt{a\cdot a}$

向量a和b的夹角 $\theta$ 为：

$\theta = cos^{-1}\frac{a\cdot b}{|a||b|}$

这样，在点积的定义下，我们就有了长度距离和角度的概念。

在点积的定义下，我们知道向量a和b的点积如下：

$a\cdot b=x_{1}x_{2}+y_{1}y_{2}+(x_{1}y_{2}+x_{2}y_{1})cos\beta$

其中(x1,y1)和(x2,y2)分别为向量a和b的坐标， $\beta$ 为基的夹角。由此可见，当夹角为90度，即基相互正交时，基夹角的余弦值为0，那么向量a和b的点积就可以简化为x1x2+y1y2，这正是我们在标准正交基下的向量点积形式。

至此，我们可以知道，当需要定义距离长度和角度时，取标准正交基可以大大简化长度和角度的定义，从而有助于简化我们的分析。而我们所学的数学，除非学到较深的抽象代数等更加专业数学学科，一般情况下，我们分析的对象往往都需要涉及到距离和角度的概念，如果时现实应用问题，那更是如此，所以我们选取的也往往都是标准正交基。长此以往，我们的大脑习惯了标准正交基上建立的直观，因此我们自己分析问题时，有时尽管不涉及长度和角度概念，我们也往往自然而然的建立标准正交基下的坐标系，从而进一步固化加强我们对标准正交基的直观和依赖。

通过本文，我们需要知道，标准正交基并不总是最恰当的，具体问题需要选取不同的坐标系统，目的是为了简化问题的分析。但是当问题的分析涉及长度距离和角度时（这是很常见的），那么我们就应该选取标准正交基，基笛卡尔坐标系统，这样可以简化长度和角度的表达，从而简化分析。