一、由内积到正交

  为了说明正交，需要先解释一种运算——内积. 内积的概念源自内积空间，下文摘自我的另一篇博客 内积空间(传送门)
  设 $V$ 是实线性空间，在其上定义了内积运算 $(\cdot ,\cdot ):V\times V\to R$，即 $\forall x,y\in V$，在 $R$ 中都有唯一的一个元素 $\delta$ 与之对应，称为 $x$ 与 $y$ 的内积，记为 $(x,y)$，且满足以下性质：

 $1.(x,x)\ge 0$ 且$(x,x)=0\iff x=0$
 $2.(x,y)=(y,x)$
 $3.(ax,z)=a(x,z),a\in R$
 $4.(x+y,z)=(x,z)+(y,z)$

则称 $(V,(\cdot ,\cdot ))$ 为内积空间.

  可以通过内积来定义向量的长度: $\Vert x\Vert =\sqrt{(x,x)}$，$\Vert kx\Vert =\sqrt{(kx,kx)}=\sqrt{k^2(x,x)}=k\Vert x\Vert$.

  长度为 1 的向量称为单位向量. 若 $\alpha \ne 0$，则由上述性质，向量 $\frac{\alpha }{\Vert \alpha \Vert }$ 就是一个单位向量，这一操作通常称为将 $\alpha$ 单位化.

  在解析几何中，向量 $\alpha ,\beta$ 的夹角 $⟨\alpha ,\beta ⟩$ 的余弦可以通过内积来表示：
$$cos⟨\alpha ,\beta ⟩=\frac{(\alpha ,\beta )}{\Vert \alpha \Vert \Vert \beta \Vert }$$为了在一般的内积空间中利用上述公式引入夹角的概念，需要先证明一个重要的不等式：
柯西-施瓦兹(Cauchy-Schwarz)不等式 (证明传送门)$$(\alpha ,\beta {)}^2\le (\alpha ,\alpha )(\beta ,\beta )$$则 $(\alpha ,\beta )\le \Vert \alpha \Vert \Vert \beta \Vert$. 若 $\alpha ,\beta$ 均不为零向量，则有 $\frac{|(\alpha ,\beta )|}{\Vert \alpha \Vert \Vert \beta \Vert }\le 1$，由此可定义两者间的夹角 $$⟨\alpha ,\beta ⟩=arccos\frac{(\alpha ,\beta )}{\Vert \alpha \Vert \Vert \beta \Vert },0\le ⟨\alpha ,\beta ⟩\le \pi .$$则内积也可以表示为: $(\alpha ,\beta )=\Vert \alpha \Vert \Vert \beta \Vert cos⟨\alpha ,\beta ⟩$.

  若两向量 $\alpha ,\beta$ 的内积 $(\alpha ,\beta )$ 为零，则称两向量相互正交.

  显然这里正交的定义与解析几何中向量垂直的说法是一致的，即两个非零向量相互正交的充要条件是它们的夹角为 $\pi /2$.

二、标准正交基

  基的概念源于线性空间. 若在线性空间 $V$ 中有 $n$ 个线性无关的向量 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$，且 $V$ 中任一向量都能由它们线性表出，则 $V$ 的维数为 $n$，并称 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$ 是 $V$ 的一组基.

  在内积空间 $V$ 中的一组非零向量，若它们两两相互正交，则称为一正交向量组.
  正交向量组 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m$ 一定线性无关，简单证明一下：

   设 $k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_m{\alpha }_m=0$
   两边同时对 ${\alpha }_i$ 作内积，则由正交性，
   左边 $=k_i({\alpha }_i,{\alpha }_i)$，右边 $=0$.
   又因为 $({\alpha }_i,{\alpha }_i)\ne 0$，所以 $k_i=0,i=1,2,\cdots ,m$，故向量组线性无关.

  于是 $n$ 维内积空间 $V$ 中，含有 $n$ 个向量的正交向量组线性无关，故形成一组基，称为正交基. 进一步，若每个向量的长度均为1，称为标准正交基.
  设 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_n$ 为一组标准正交基，由定义，有
$$({ϵ}_i,{ϵ}_j)={\delta }_{ij}=\{\begin{array}{l}1,i=j\\ 0,i\ne j\end{array}$$

三、标准正交基，你有什么好？

标准正交基下：

1. 向量的坐标可以通过内积简单求出
   设 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_n$ 为 $V$ 中的一组标准正交基，$\alpha$ 为 $V$ 中任一向量，则 $\alpha$ 可以表示成 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_n$ 的线性组合，即$$\alpha =k_1{ϵ}_1+k_2{ϵ}_2+\cdots +k_n{ϵ}_n$$所谓坐标，就是向量在基下的组合系数，即 $(k_1,k_2,\cdots ,k_n)$
   用 $ϵ$ 与等式两边作内积，由标准正交基的定义，有 $(\alpha ,{ϵ}_i)=k_i,i=1,2,\cdots ,n$，于是$$\alpha =(\alpha ,{ϵ}_1){ϵ}_1+(\alpha ,{ϵ}_2){ϵ}_2+\cdots +(\alpha ,{ϵ}_n){ϵ}_n.$$

2. 向量之间的内积可以通过坐标简单表示
   设 $$\begin{array}{rl}& \alpha =x_1{ϵ}_1+x_2{ϵ}_2+\cdots +x_n{ϵ}_n\\ & \beta =y_1{ϵ}_1+y_2{ϵ}_2+\cdots +y_n{ϵ}_n\end{array}$$则$$(\alpha ,\beta )=x_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n$$记 $X=(x_1,x_2,\cdots ,x_n{)}^T,Y=(y_1,y_2,\cdots ,y_n{)}^T$，
   则 $(\alpha ,\beta )=X^{T}Y=Y^{T}X.$
   这个表达式正是几何中向量的内积在直角坐标系下坐标表达式的推广.

四、由基到标准正交基

  既然标准正交基这么好，那怎样才能得到一组标准正交基. 下面这个定理给出了答案：

  对于 $n$ 维内积空间任意一组基 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n$，都可以找到一组标准正交基 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_n$，使得
s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ i } = s p a n { α 1 , α 2 , ⋯ , α i } , i = 1 , 2 , ⋯ , n span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_i\rbrace=span\lbrace\alpha_1, \alpha_2,\cdots,\alpha_i\rbrace,i=1,2,\cdots,n span{ϵ1​,ϵ2​,⋯,ϵi​}=span{α1​,α2​,⋯,αi​},i=1,2,⋯,n即 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_i$ 与 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_i$ 可以互相线性表出.

证明：
采用构造的方式，给出标准正交基的求法，利用数学归纳法：

(1) 首先，取$${ϵ}_1=\frac{{\alpha }_1}{\Vert {\alpha }_1\Vert }$$则 ${ϵ}_1$ 与 ${\alpha }_1$ 可以相互线性表出，且为单位向量.

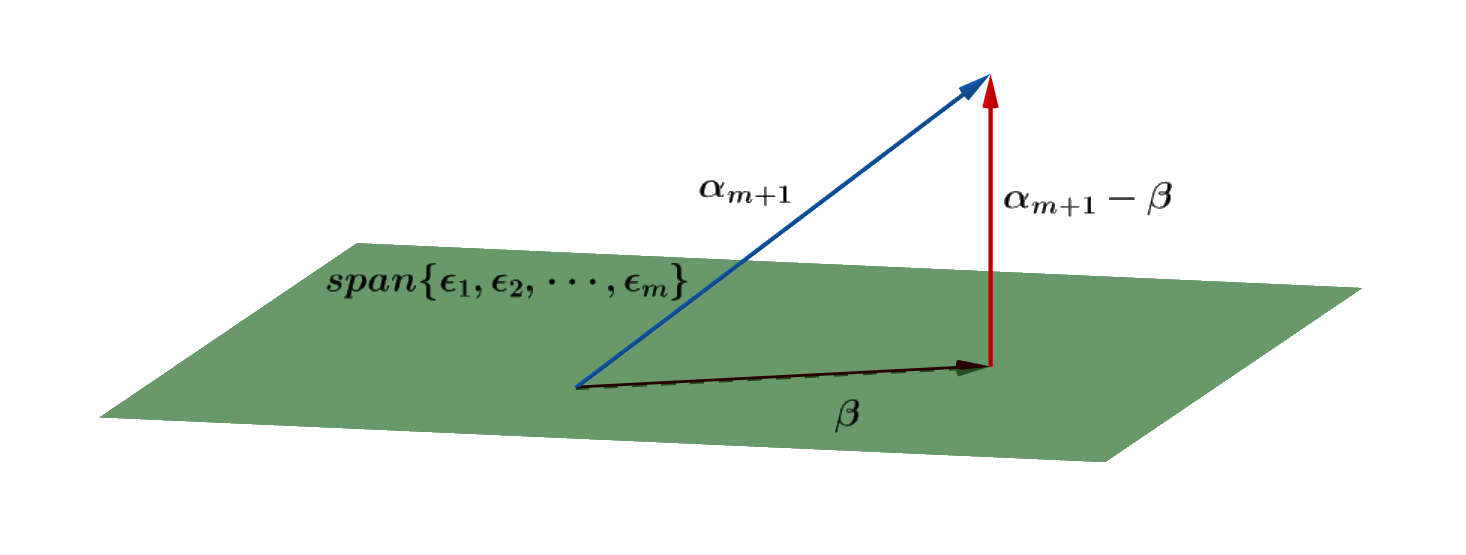
(2) 其次，假设已经求出 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_m$，它们是单位正交的，具有性质 s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ m } = s p a n { α 1 , α 2 , ⋯ , α m } span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_m\rbrace=span\lbrace\alpha_1, \alpha_2,\cdots,\alpha_m\rbrace span{ϵ1​,ϵ2​,⋯,ϵm​}=span{α1​,α2​,⋯,αm​}下一步，求 ${ϵ}_{m+1}$.

${ϵ}_{m+1}$ 应当与 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_m$ 正交，且为单位向量，且需满足 s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ m + 1 } = s p a n { α 1 , α 2 , ⋯ , α m + 1 } span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_{m+1}\rbrace=span\lbrace\alpha_1, \alpha_2,\cdots,\alpha_{m+1}\rbrace span{ϵ1​,ϵ2​,⋯,ϵm+1​}=span{α1​,α2​,⋯,αm+1​}则 ${\alpha }_{m+1}$ 可以由 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_{m+1}$ 线性表出.

这样选取 ${ϵ}_{m+1}$：
作 ${\alpha }_{m+1}$ 在空间 s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ m } span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_m\rbrace span{ϵ1​,ϵ2​,⋯,ϵm​} 上的投影，记作
$$\beta =k_1{ϵ}_1+k_2{ϵ}_2+\cdots +k_m{ϵ}_m$$则 ${\alpha }_{m+1}-\beta$ 与 s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ m } span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_m\rbrace span{ϵ1​,ϵ2​,⋯,ϵm​} 正交，
则 ${\alpha }_{m+1}-\beta$ 与 ${ϵ}_i,i=1,2,\cdots ,m$ 正交，即 $({\alpha }_{m+1}-\beta ,{ϵ}_i)=0$，
将 $\beta =k_1{ϵ}_1+k_2{ϵ}_2+\cdots +k_m{ϵ}_m$ 代入，整理得
$$({\alpha }_{m+1}-k_i{ϵ}_i,{ϵ}_i)=0$$于是 $k_i=({\alpha }_{m+1},{ϵ}_i),i=1,2,\cdots ,m$，取 $${ϵ}_{m+1}=\frac{{\alpha }_{m+1}-\beta }{\Vert {\alpha }_{m+1}-\beta \Vert }$$则 ${ϵ}_1,{ϵ}_2,\cdots ,{ϵ}_{m+1}$ 是一正交向量组，且满足
s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ m + 1 } = s p a n { α 1 , α 2 , ⋯ , α m + 1 } span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_{m+1}\rbrace=span\lbrace\alpha_1, \alpha_2,\cdots,\alpha_{m+1}\rbrace span{ϵ1​,ϵ2​,⋯,ϵm+1​}=span{α1​,α2​,⋯,αm+1​} (3) 由归纳法原理，定理得证.

注：由 s p a n { ϵ 1 , ϵ 2 , ⋯ , ϵ i } = s p a n { α 1 , α 2 , ⋯ , α i } , i = 1 , 2 , ⋯ , n span\lbrace\epsilon_1,\epsilon_2,\cdots,\epsilon_i\rbrace=span\lbrace\alpha_1, \alpha_2,\cdots,\alpha_i\rbrace,i=1,2,\cdots,n span{ϵ1​,ϵ2​,⋯,ϵi​}=span{α1​,α2​,⋯,αi​},i=1,2,⋯,n 可知，两组基之间的过渡矩阵是上三角形的.


参考文献：北京大学数学系前代数小组. 高等代数[M]. 第四版. 北京：高等教育出版社，2013.

Plus: 如有错误、可以改进的地方、或任何想说的，请在评论区留言！