1.正交向量组
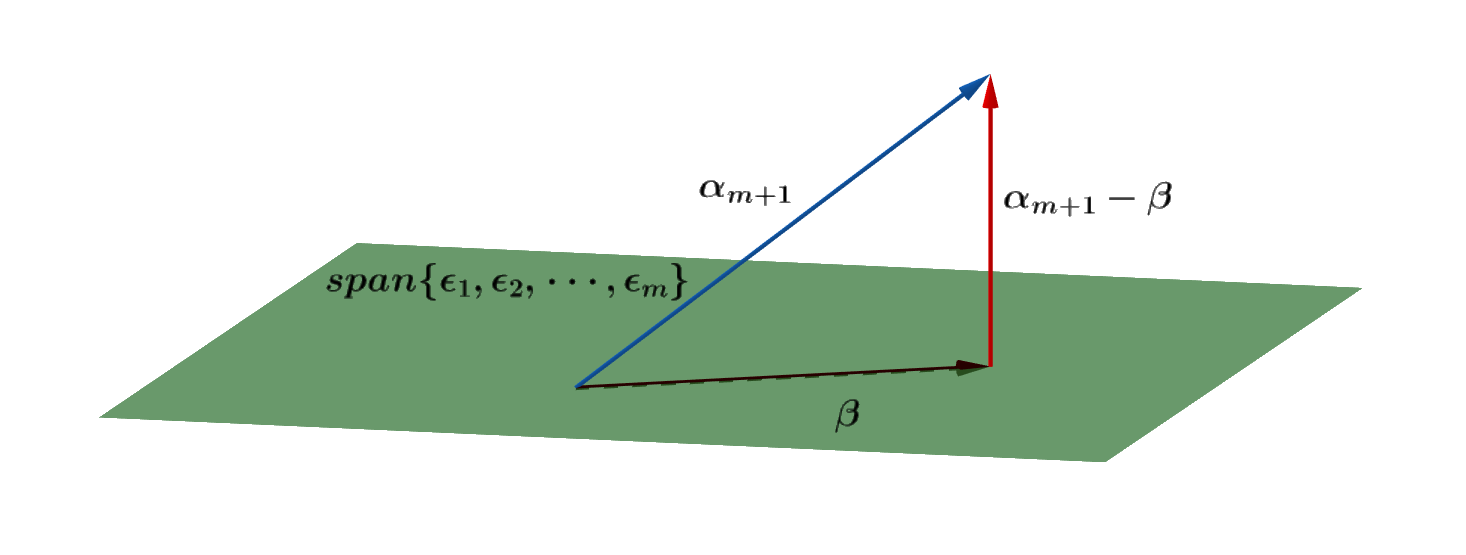
直接给定义:欧式空间V的一组非零向量,如果他们俩俩向量正交,则称是一个正交向量组。
(1)正交向量组 是 线性无关的
(2)n维欧式空间中俩俩正交的非零向量不会超过n个,即n维欧式空间中一个正交向量组最多n个向量
2.正交基
在n维欧式空间中,由n个非零向量组成的正交向量组称为正交基
3.标准正交基
在n维欧式空间中,由n个单位向量组成的正交向量组称为标准正交基
比如3维欧式空间中,
(1,0,0)、(0,1,0)、(0,0,1)是一个正交向量组,因为他们俩俩向量正交
(1,0,0)、(0,1,0)、(0,0,1)是一个正交基,因为此正交向量组由n个非零向量组成
(1,0,0)、(0,1,0)、(0,0,1)是一个标准正交基,因为每个向量都是单位向量
4.单位矩阵
如果一个矩阵满足一下几个条件,它就是一个单位矩阵,记作E或者I:
(1)是一个方阵
(2)主对角线上的元素都是1(主对角线是从左上到右下的对角线)
(3)除了主对角线,其他位置的元素都是0
如下就是一个3阶单位矩阵
[[1 0 0][0 1 0][0 0 1]]4.正交矩阵
The orthogonal matrix,正交矩阵,如果一个矩阵满足以下几个条件,则此矩阵就是正交矩阵:
(1)是一个方阵
(2)和自己的转置矩阵的矩阵乘积 = 单位矩阵E
如果A为一个正交矩阵,则A满足以下条件:
1) A的转置矩阵也是正交矩阵
2) ![]() (E为单位矩阵)
(E为单位矩阵)
3) A的各行是单位向量且两两正交
4) A的各列是单位向量且两两正交
5) (Ax,Ay)=(x,y) x,y∈R
6) |A| = 1或-1
7) ![]() ,A的转置矩阵等于A的逆矩阵
,A的转置矩阵等于A的逆矩阵
5.正交变换
内积定义:u,v的内积=|u||v|cos<u,v>
在线性代数中,正交变换是线性变换的一种,它从实内积空间V映射到V自身,且保证变换前后内积不变。
因为向量的模长与夹角都是用内积定义的,所以正交变换前后一对向量各自的模长和他们的夹角都不变。
特别地:标准正交基经正交变换后仍为标准正交基。
欧式空间V中的正交变换只包含:
(1)旋转
(2)反射
(3)旋转+反射的组合(即瑕旋转)
正交变换T的性质
原矩阵A:[[1 2 3][4 5 6][7 8 9]]
正交变换T:[[2 0 0][0 3 0][0 0 4]]
A经过T变换的矩阵TA:[[ 2 4 6][12 15 18][28 32 36]]可知
[2,0,0]中的2是将A中[1,2,3]向量"拉长"一倍得到[2,4,6]
[0,3,0]中的3是将A中[4,5,6]向量"拉长"三倍得到[12, 15, 18]
[0,0,4]中的4是将A中[7,8,9]向量"拉长"四倍得到[28, 32, 36]
这个是拉伸,如果T中主对角线上的值是小数,则表示将A中对应向量“缩小”一定比例
如果T中主对角线位置外的其他位置上的元素不为0,则表示对A进行一定方向的旋转
这些概念在图像处理里面显得更为重要,可以看看OpenCV中的几何变换,就是用变换矩阵乘上原矩阵得到目标矩阵。
(end)