一、问题描述

八皇后问题的目标是在国际象棋棋盘中放置8个皇后，使得任何一个皇后都不会攻击到其他任一皇后。(皇后可以攻击和它在同一行，同一列或者同一对角线的任何棋子)

二、编程语言及算法

编程语言：python

算法：遗传算法

三、求解思路

1、种群初始化

首先要对个体进行初始化，对于第 $i$ 列，编码为 $x$ ，表示第 $i$ 列的第 $x$ 行有一个皇后，编号从 $0$ 开始。

对于一个个体，则可以用 $8$ 个编码来表示。

示例：下图的棋盘即可以用编码 $06471352$ 来表示：

在初始化时，采用完全随机的方式进行编码，即对于每一列设置的编码都是随机的，

# 生成一个体individual
for i in range(8):a = random.randint(0, 7)individual.append(a)

初始种群设置为 $4$ 个个体，我们便生成 $4$ 个个体加入到种群中，从而完成种群的初始化。

# 计算生成的个体的适应度
fit_score = update_fitness_score(individual)
# 加入到种群中
parent_fitness.append(fit_score)
parent.append(individual)

2、适应度函数

适应度函数表示为：不互相攻击的皇后对的数目

那么当满足题目要求时，8个皇后都不互相攻击，共有 $8\times 7/2=28$ 对，即当出现适应度为28时，程序便可以结束。

那么如何对该程序进行实现呢？

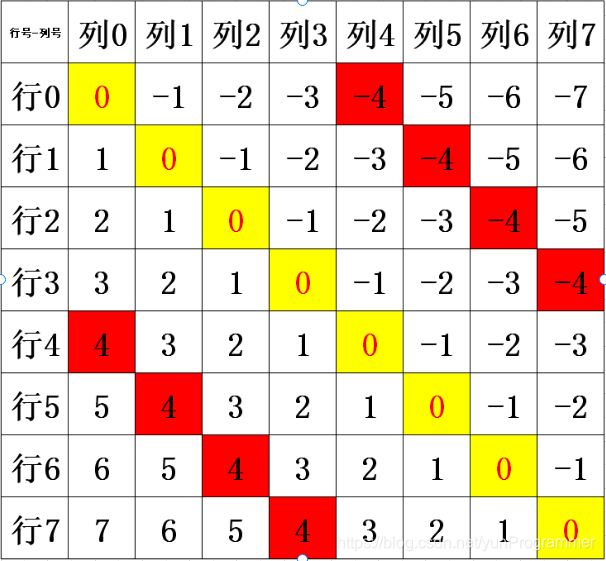
选择两个列（为避免重复运算，人为规定第一个列数小于第二个列数，如果这两个编码不相等，说明这两个皇后不在同一行，我们再判断两个列数的绝对值与对应的两个编码的绝对值是否相等，如果不相等，这说明两个皇后不在同一列，这时我们把适应度值 $+1$ 。这样适应度函数便设计完毕。

def update_fitness_score(individual):value = 0for i in range(8):for j in range(i + 1, 8):if individual[i] != individual[j]:x = j - iy = abs(individual[i] - individual[j])if x != y:value += 1return value

3、如何选出两个父本

根据概率大小，在一个区域上根据适应度函数的大小划定不同的范围，此时在区域内生成一个随机数，该随机数落在谁的范围，那么就代表选择谁。重复两次，选择两个父本。

4、如何选取杂交点

随机选取两个点组成一个区间，将两个父本在该区间的基因进行交换

4、如何变异

自然中，变异是有一定的概率的，我们假设本题中的概率为$50\%$，生成一个在 $0-1$ 之间的随机浮点数，如果该浮点数大于0.5，则进行变异。

变异的形式为基因突变，即在某个点的基因随机变为 $0-7$ 中的一个。

四、程序运行结果

由于遗传算法模拟了自然选择中的遗传变异等行为，算法中加入了多个依靠概率运行的逻辑，在测试中，最少只用了 $1000$ 多次迭代便得出了结果，最多用了十万多次才得出结果，不排除会出现几十万次甚至上百万次才出结果的情况。

对于本题来说，利用回溯算法做会更加简单且效率高，但对于一些更复杂的问题，难以通过一些固定的算法进行求解，那么采用遗传算法便可以明显降低算法复杂度且编写代码较容易。

五、代码

import copy
import random
import math# 种群大小
population_size = 8
# 父种群的编码列表
parent = []
# 子种群的编码列表
children = []
# 父种群每个个体的适应度
parent_fitness = []
# 子种群每个个体的适应度
children_fitness = []# 初始化个体
def initial_individual():# 个体的编码individual = []# 8个编码for i in range(8):a = random.randint(0, 7)individual.append(a)# 计算生成的个体的适应度fit_score = update_fitness_score(individual)# 加入到种群中parent_fitness.append(fit_score)parent.append(individual)return# 更新适应度函数
def update_fitness_score(individual):value = 0for i in range(8):for j in range(i + 1, 8):if individual[i] != individual[j]:x = j - iy = abs(individual[i] - individual[j])if x != y:value += 1return value# 初始化1个种群,种群大小为population_size
def initial_population():for i in range(population_size):initial_individual()return# 选择出一个父本
def select():# 所有个体的适应度之和total_score = 0for fit in parent_fitness:total_score += fit# 轮盘赌中的数num = random.randint(0, total_score)# 前面的适应度之和front_score = 0for i in range(population_size):front_score += parent_fitness[i]# 如果此时前面的适应度之和大于生成的随机数，那么该数必定落在编号为 i 的个体上if front_score >= num:return i# 变异
def mutation(change_individual):# 第pos个基因发生变异pos = random.randint(0, 7)# 改变的值change = random.randint(0, 7)change_individual[pos] = changereturn change_individual# 交叉产生后代
def hybridization():# 选择两个父本first = select()second = select()selected_parents = copy.deepcopy([parent[first], parent[second]])# 交换从pos1到pos2的基因pos1 = random.randint(0, 6)pos2 = random.randint(0, 6)# 保证pos1 <= pos2if pos1 > pos2:pos1, pos2 = pos2, pos1# 交叉tmp = selected_parents[0][pos1:pos2]selected_parents[0][pos1:pos2] = selected_parents[1][pos1:pos2]selected_parents[1][pos1:pos2] = tmp# 一定的概率发生变异,假设概率为0.5may = random.random()if may > 0.5:selected_parents[0] = mutation(selected_parents[0])may = random.random()if may > 0.5:selected_parents[1] = mutation(selected_parents[1])# 更新适应度first_fit = update_fitness_score(selected_parents[0])second_fit = update_fitness_score(selected_parents[1])# 加入到子代中children.append(selected_parents[0])children.append(selected_parents[1])children_fitness.append(first_fit)children_fitness.append(second_fit)return# 初始化种群
initial_population()
# 计算迭代次数
count = 0
# not a number
find = float('nan')
while True:count += 1if count % 1000 == 0:print('第%d' % count + '次迭代')# 杂交population_size/2次产生population_size个后代for k in range(population_size // 2):hybridization()# 如果某个个体适应度达到28，说明此时找到了一个解for k in range(population_size):if children_fitness[k] == 28:# 记录解的位置find = kbreakif not math.isnan(find):break# 将子代种群放入父代中作为新的父代，子代清空parent[0:population_size] = children[0:population_size]parent_fitness[0:population_size] = children_fitness[0:population_size]children = []children_fitness = []# 此时找到满足要求的子代个体
res = children[find]
print(res)# 构造棋盘
res_queen = [[0 for i in range(8)] for j in range(8)]
for t in range(8):res_queen[res[t]][t] = 1
# 将棋盘打印
print("找到结果：")
for t in range(8):print(res_queen[t])