题目描述

• 在8×8格的棋盘上放置彼此不受攻击的8个皇后。国际象棋的规则：皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子
  

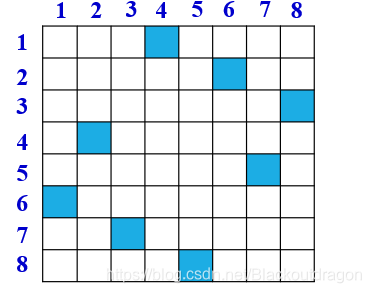
思路分析

• 八皇后问题等价于，在8*8格的棋盘上放置8个皇后， 任何两个皇后皇后不得在同一行或者同一列或者同一斜线上

回顾回溯法的基本框架

• 首先定义问题的解空间：给出问题的所有解和最优解。在我理解，就是给出将问题使用另外一种可编程的形式表达出来。
• 确定易于搜索的解空间结构：
  • 两种树型结构：
    • 子集树：问题是从n个元素的集合中找出满足性质的k个元素的集合，是组合问题
    • 排列树：确定n个元素的满足某种性质的排列，使用排列树。
  • 确定约束函数，两种方式，一种是约束函数，另外一种是限界函数
    • 约束函数，在扩展结点处减去不满足约束的子树。
    • 限界函数，减去得不到最优解的子树。
• 从根节点出发，以深度优先的方式搜索解空间树，算法搜索到空间树的任意一点。

解题框架应用到本题

定义问题的解空间

• 定义解空间，使用可编程形式去定义问题。将问题转换成的一维数组去表示，值表示对应的列，位序表示行！
  
  
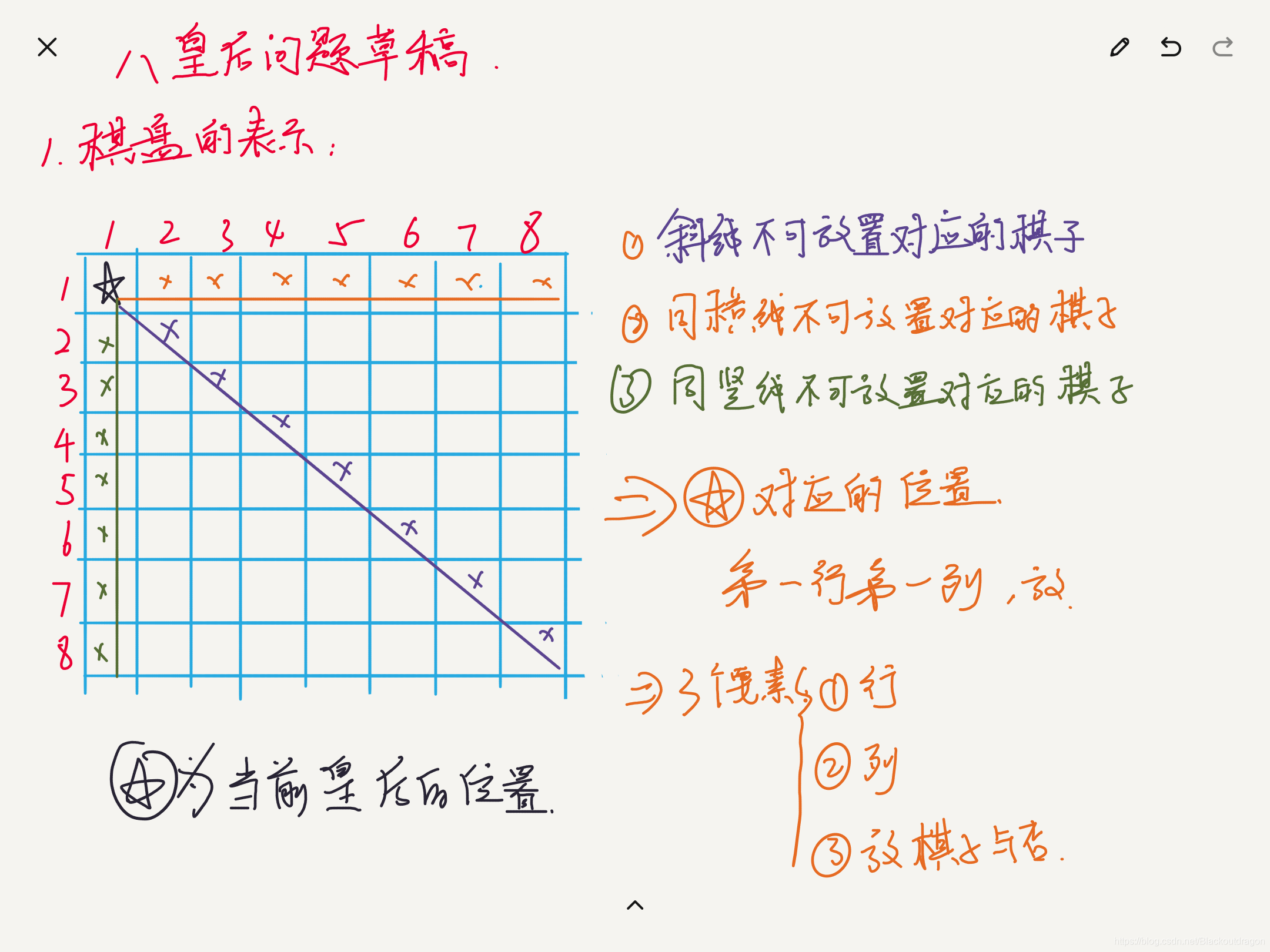
• 如果我没有看过课本，我会默认使用二维数组去解决这个问题，而不是一位数组，如果使用二维数组会遇到很多的问题。

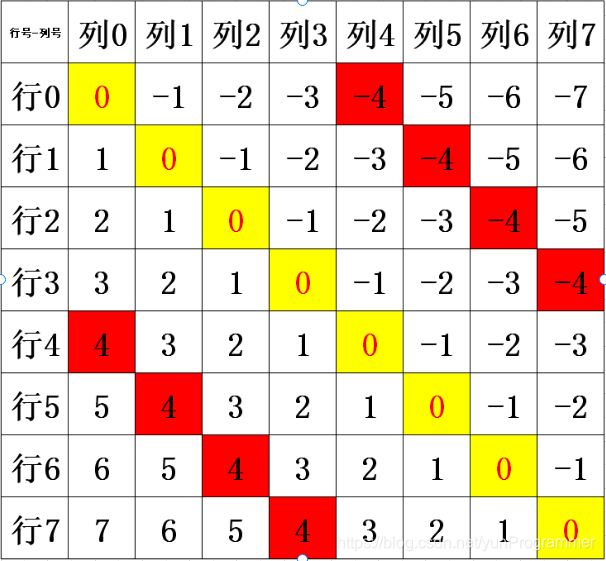
定义约束函数

• 主要是三个：
  • 不同行
  • 不同列
  • 不同斜线

模仿回溯法的框架去解决问题

void backtrack(int t)
{if (t>n) output(x);elsefor (int i=f(n,t);i<=g(n,t);i++) {x[t]=h(i);if (constraint(t)&&bound(t)) backtrack(t+1);}
}

• t表示递归深度，n表示最大递归深度，这也是控制层数
• output(x):表示输出可行解x
• for循环遍历起始点和终止点
• 只有符合约束条件，才会进行下一步迭代

实现源码

#include<iostream>using namespace std;//定义一个一维的数组去表示问题，在递归的过程中可以操控，所以必须是全局变量
//这里定义九个，第一个是不可以用的，索引是零
int queen[9];
//定义一个total变量，保存所有的八皇后的数量
int total = 0;/*描述：约束函数，判定传入当前的状态是否符合条件参数：row，行号返回：当前的位置能不能放皇后理解：给我行号我就能根据索引找到对应数组的值，获取对应列号判定之前几个皇后的位置是否与当前皇后的位置冲突
*/
bool constrain(int row) {for (int i = 1; i < row; ++i){if (queen[i] == queen[row] || abs(row - i) == abs(queen[row] - queen[i])){//只要相等，就立即返回falsereturn false;}}return true;
}/*描述：回溯法递归选项，通过递归实现树的结构的遍历参数：n 树的的层数，也是递归的深度，皇后的个数，也是行号返回：无返回值，仅仅只有递归描述：递归传的参数一定要有递归终止的条件参数
*/
void recursive(int row) {for (int i = 1; i < 9; i++) {cout << queen[i] << "  ";}cout << endl;//先列上递归终止的条件if (row == 9){total++;}else {//在列上迭代的条件for (int col = 1; col < 9; ++col){//改变当前的状态//第row行的第col列，放上对应的皇后queen[row] = col;//判定当前的环境是否满足约束条件//只需要传入行号，即可以获取当前的状态if (constrain(row)){//符合条件就进行下一个递归recursive(row + 1);}}}
}int main(int argc, char const* argv[])
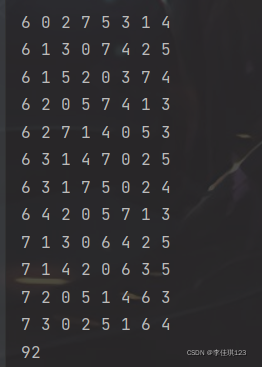
{//从第一行的第一列开始遍历recursive(1);cout << total << endl;int a;cin >> a;return 0;
}

分析与总结

• 这是回溯算法一个简单的应用，是一个很好的尝试！回溯算法还是很普适的！