八皇后问题（英文：Eight queens），是由国际象棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。

问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。

首先是解题的思路：for循环的嵌套  遍历每一种结果

 //依次放入皇后 判断是否冲突for (int i = 0; i < max; i++) {array[n]=i;if (judge(n)){check(n+1);}//如果不冲突就继续执行array[n]=i 即将第n个皇后 放置在本行后移的一个位置}

解题思路详解： 

放置皇后的时候 n=0;直接开始第一次for循环 将一个行的第一个位置放置一个皇后 然后开始第二次for循环 进入第二次for循环的时候n已经+1开始遍历第二行  知道与第一个不冲突 开始第三次for循环 一样的道理 知道第三个与第一个和第二个都不冲突放入 直到放完最后一个 开始回溯 假如中途退出 比如放置第三个的时候每个位置都行不通 就会直接回溯 找出第二个还能放置的位置 在进入遍历第三个 放完一次 回溯到上一位 让上一位换个位置 在进入 让下一位接着遍历每一次 知道前面7个位置所有的方式都遍历完之后 首位才会发生改变  这就是输出结果为什么首位都是按序排列 因为 每一位的每一种可能都考虑到了。

开始的流程图解如下 

回溯的时候差不多大致相同

 

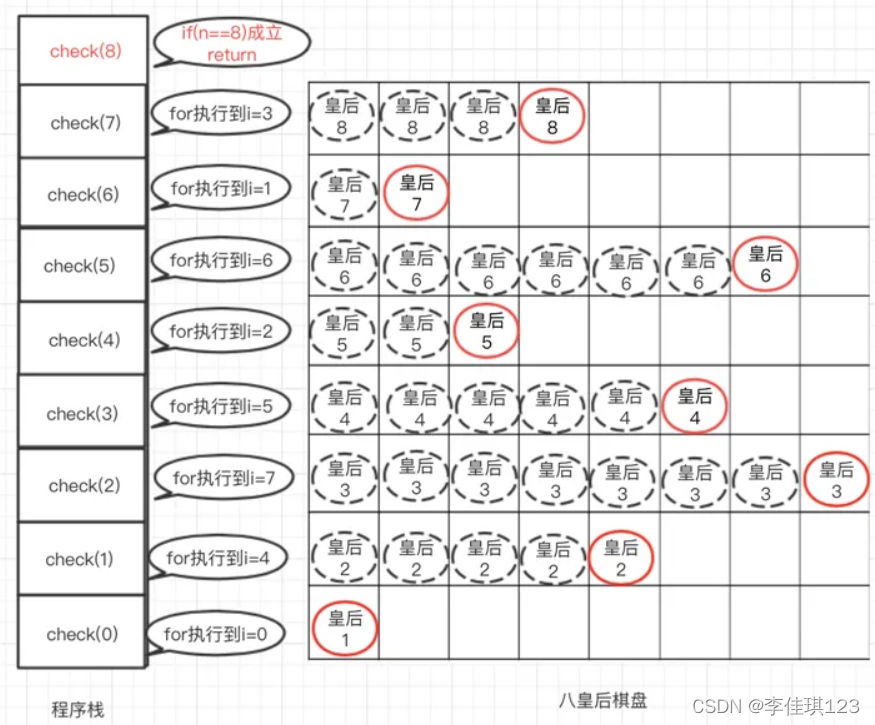
 这里到达顶层了 他会回到皇后7这里 让他后移一位 然后继续回到皇后8 从头遍历看看还有没有合适的解答 假如没有就会回到7 7往后遍历 然后再进8 都没有之后就会进入6 6遍历后移再进7 知道回溯到皇后1 皇后1后移继续开始最开始的流程往上走 走到头再像老样子往后走。

解释完  这里直接放代码了

定义一个输出方法

   /*** 定义一个方法输出每个皇后的位置*/public void print(){count++;for (int i = 0; i < array.length; i++) {System.out.print(array[i]+" ");}System.out.println("");}

然后定义检查是否能放置的方法

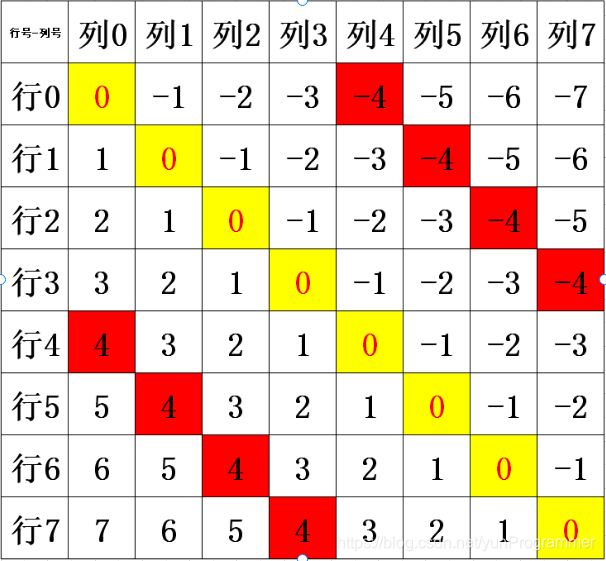
    /**** @param n n表示第n+1个皇后 第n+1行的第几个位置*          如array[1] 表示第二行的皇后在第二行的哪个位置* @return 方法是为了确定下一个皇后放在这冲不冲突*/private boolean judge(int n){//i 第i+1个皇后的下标  array[i]表示第i+1行的皇后在哪个位置for (int i = 0; i < n; i++) {//array[i]==array[n] 表示在同一行//重点解释在不在同一斜线的情况  首先要知道达成什么条件在一直线上//这里不卖关子 要知道假如两点连线与水平线形成45度角 在8*8宫格中则在同一直线上//怎么表示两点的夹角 这里Math.abs(n-i)表是行差 Math.abs(array[n]-array[i])表示列差//行差等于列差的时候就代表在一条斜线上 45度夹角 类比正方形if (array[i]==array[n] || Math.abs(n-i) == Math.abs(array[n]-array[i])){return false;}}return true;}

然后放置皇后的方法

    /*** 编写一个方法放置皇后**/public void check(int n){//如果放置完第八个皇后就打印if (n == max){print();return;}//依次放入皇后 判断是否冲突for (int i = 0; i < max; i++) {array[n]=i;if (judge(n)){check(n+1);}//如果不冲突就继续执行array[n]=i 即将第n个皇后 放置在本行后移的一个位置}}

最后主类和运行代码

    static int count = 0;/*** max表示有多少行* 这里用一维数组表示棋牌* 数组的最大容度就是有多少行* 下标+1表示哪行 每个数值表示每行的第几个 就是第几列*/int max = 8;int [] array = new int[max];public static void main(String[] args) {Queen8 queen8 = new Queen8();queen8.check(0);System.out.println(count);}

完整版

package Recursion;/*** @author:LeeGaki* @date:2022/4/26*/
public class Queen8 {static int count = 0;/*** max表示有多少行* 这里用一维数组表示棋牌* 数组的最大容度就是有多少行* 下标+1表示哪行 每个数值表示每行的第几个 就是第几列*/int max = 8;int [] array = new int[max];public static void main(String[] args) {Queen8 queen8 = new Queen8();queen8.check(0);System.out.println(count);}/*** 编写一个方法放置皇后**/public void check(int n){//如果放置完第八个皇后就打印if (n == max){print();return;}//依次放入皇后 判断是否冲突for (int i = 0; i < max; i++) {array[n]=i;if (judge(n)){check(n+1);}//如果不冲突就继续执行array[n]=i 即将第n个皇后 放置在本行后移的一个位置}}/**** @param n n表示第n+1个皇后 第n+1行的第几个位置*          如array[1] 表示第二行的皇后在第二行的哪个位置* @return 方法是为了确定下一个皇后放在这冲不冲突*/private boolean judge(int n){//i 第i+1个皇后的下标  array[i]表示第i+1行的皇后在哪个位置for (int i = 0; i < n; i++) {//array[i]==array[n] 表示在同一行//重点解释在不在同一斜线的情况  首先要知道达成什么条件在一直线上//这里不卖关子 要知道假如两点连线与水平线形成45度角 在8*8宫格中则在同一直线上//怎么表示两点的夹角 这里Math.abs(n-i)表是行差 Math.abs(array[n]-array[i])表示列差//行差等于列差的时候就代表在一条斜线上 45度夹角 类比正方形if (array[i]==array[n] || Math.abs(n-i) == Math.abs(array[n]-array[i])){return false;}}return true;}/*** 定义一个方法输出每个皇后的位置*/public void print(){count++;for (int i = 0; i < array.length; i++) {System.out.print(array[i]+" ");}System.out.println("");}
}

运行结果如下：

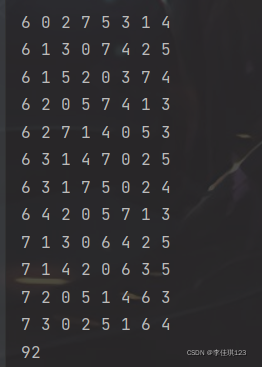 太长了截不全 共92种解就对了。