八皇后问题是回溯算法里面的经典问题，起源于1848年由国际西洋棋手马克斯，贝瑟尔提出，1850年法国著名的数学家高斯提出共有76种解法，实际上真的是这样吗，多年后我们通过计算机程序可以发现真正的解法比76种更多。

问题描述：

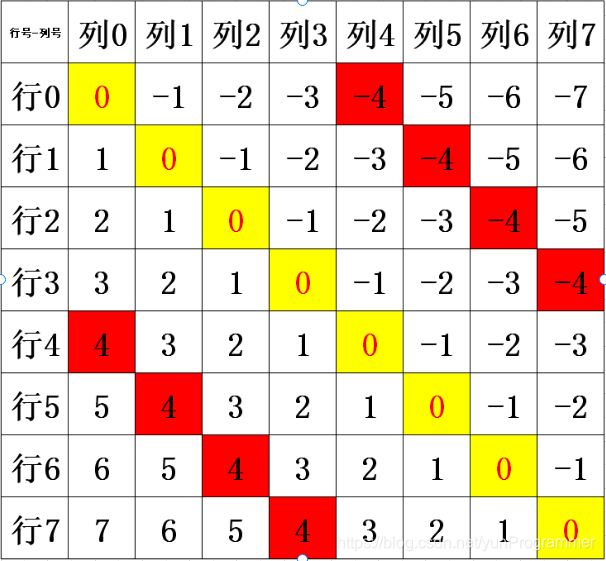
棋盘中皇后可以攻击同一行、同一列，或者左上、左下、右上、右上四个方向的任意单位。现在给你一个N*N的棋盘，让你防止N个皇后，使得他们不得相互攻击，返回所有合法的结果。

今天我们来分析一下八皇后问题的解题思路。

N皇后是使用回溯算法的典型问题，需要从第一行第一列开始，防止第一个皇后，然后第二列找合适的位置，然后在第三列找合适的位置放三个皇后，如果发现第三个没有防止的合适的位置，需要回溯到之前的位置，然后在把第一个皇后放到第一行第二列，在第二排在寻找合适的位置，然后是第三列，第四列。。。。。。通过此种方式可以找到所有的解法。

假设N==4，我们穷举所有的解法，可以得到下面的两种解法。

代码（LeetCode版）如下：

class Solution {
public:vector<vector<string>> res; vector<vector<string>> solveNQueens(int n) {vector<string> board(n, string(n, '.'));backtrack(board, 0);return res;}void backtrack(vector<string>& board, int row){if (row == board.size()){res.push_back(board);return;}int n = board[row].size();for(int col=0; col<n;col++){//排除不合法的选择if(!isValid(board, row, col))continue;board[row][col] = 'Q';backtrack(board, row+1);board[row][col] = '.';}}bool isValid(vector<string>&board, int row, int col){int n = board.size();for (int i=0;i<row;i++){if(board[i][col]=='Q')return false;}// 右上方for (int i = row-1,j=col+1; i>=0 && j<n; i--,j++){if (board[i][j] == 'Q')return false;}//左上方for (int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(board[i][j] == 'Q')return false;}return true;}
};

跑完之后，我们会发现总共有92种解法，具体的大家可以用编译器跑一跑。