1. 八皇后的由来和问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种计算机语言可以解决此问题。
2. 问题的解决思想
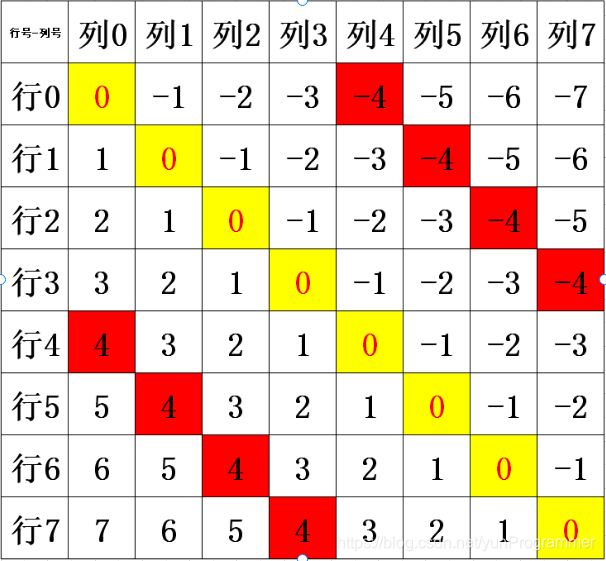
先来打印一个棋盘,这里举例用八行八列来说。首先,每一行就只有一个皇后,而且各行的皇后不能同时出现在一个米字型的表格中。

假如图中的 * 是一个皇后,那么所有粉色的圆圈都不能有皇后。
好了,看图。

这也是一种回溯算法。
下面来摆上代码,我来一步一步的解释代码。
- 首先初始化棋盘,8*8的棋盘,再增加一圈,给最外圈加一圈 ‘#’。棋盘中全部赋值为空格。
#define N 8
char board[N+2][N+2];
void Init(void)
{for (int row = 0; row < N + 2; row++){for (int col = 0; col < N + 2; col++){board[0][col] = '#';board[N + 1][col] = '#';board[row][0] = '#';board[row][N + 1] = '#';}}for (int i = 1; i <= N; i++){for (int j = 1; j <= N; j++){board[i][j] = ' ';}}
}- 检查函数,判断棋盘中那个位置能否放皇后
int Check(int row, int col)
{int ret = 1;int nr;int nc;for (int i = 0; i < 3 && ret; i++){nr = row;nc = col;while (ret&&board[nr][nc] != '#'){if (board[nr][nc] == '*'){ret = 0;break;}nr = nr + pos[i].yos;nc = nc + pos[i].xos;}}return ret;
}- 给棋盘中放 ‘*’ ,调用检查函数,看看是否可以放进去,如果哪一行都不能放,那么就调换上一行中的位置,(回溯算法),也用到了递归的思想。
void Find(int row)
{if (row>N){Show();count++;printf("%d\n",count);}else{for (int col = 1; col <= N; col++){if (Check(row, col)){board[row][col] = '*';Find(row + 1);board[row][col] = ' ';}}}
}- 展示函数,用于展示所放的 ‘*’ ,用来展示棋盘。
void Show(void)
{for (int i = 0; i < N + 2; i++){for (int j = 0; j < N + 2; j++){printf("%c", board[i][j]);}printf("\n");}
}最后附上所有源代码。
#include<stdio.h>#define N 8
char board[N+2][N+2];
int count = 0;struct Pos
{int yos; //行偏移量int xos; //列偏移量
};struct Pos pos[3] = { { -1, -1 }, { -1, 0 }, { -1, 1 } };void Init(void)
{for (int row = 0; row < N + 2; row++){for (int col = 0; col < N + 2; col++){board[0][col] = '#';board[N + 1][col] = '#';board[row][0] = '#';board[row][N + 1] = '#';}}for (int i = 1; i <= N; i++){for (int j = 1; j <= N; j++){board[i][j] = ' ';}}
}void Show(void)
{for (int i = 0; i < N + 2; i++){for (int j = 0; j < N + 2; j++){printf("%c", board[i][j]);}printf("\n");}
}int Check(int row, int col)
{int ret = 1;int nr;int nc;for (int i = 0; i < 3 && ret; i++){nr = row;nc = col;while (ret&&board[nr][nc] != '#'){if (board[nr][nc] == '*'){ret = 0;break;}nr = nr + pos[i].yos;nc = nc + pos[i].xos;}}return ret;
}void Find(int row)
{if (row>N){Show();count++;printf("%d\n",count);}else{for (int col = 1; col <= N; col++){if (Check(row, col)){board[row][col] = '*';Find(row + 1);board[row][col] = ' ';}}}
}int main()
{Init();Find(1);system("pause");}