【算法模板】dfs 八皇后问题

article/2025/9/15 8:36:00

1.前言

本文将以经典的八皇后问题来解析dfs的主要思想。

2.题目

题目出处：活动 - AcWing

3.思路讲解

dfs的思想暗含树的历遍，主要步骤为：

判断是否搜索完毕---历遍寻找符合条件的元素---递归进入下一层搜索---还原现场

我们可以先分析这个问题，发现皇后在每一行只能有一个，并且对角线，反对角线，每一排，每一列都只有一个皇后。

那么我们就可以从底层出发，遍历一排中的每一个元素，然后深入搜索下一排符合条件的元素，搜索到最后时，即是符合条件的第一个答案，回溯到第一排的下一个元素进行搜索。

由于dfs的灵魂是递归，所以递归的知识一定要掌握清楚。

4.代码实现

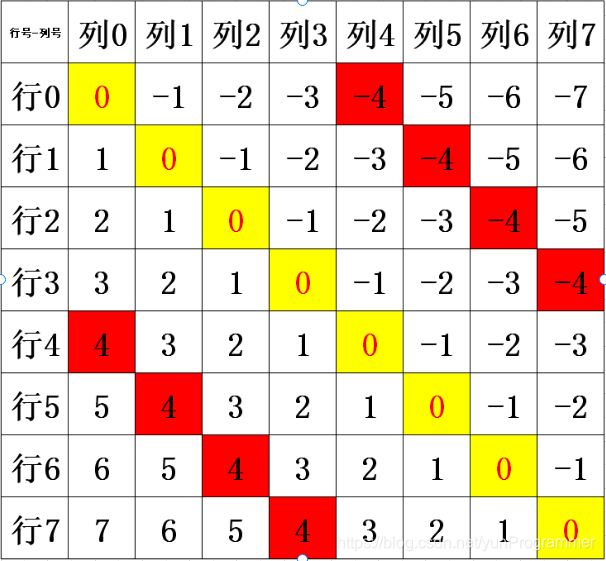
参照以下网格来理解代码:

该方法符合dfs的一般做法，当然算法是死的，人是活的，依照不同的题目，dfs的参数，形式等多种多样，不敢一板子把代码论死。要参照思想，具体情况具体分析，dfs最重要的便是顺序！！！

4.1 法1

#include <iostream>
using namespace std;
const int N = 20;//定义图（网格）
char path[N][N];//col记录每一列的皇后数，确保只有1个
//dg记录正对角线的皇后数，确保只有1个
//udg记录反对角线的皇后数，确保只有1个
bool col[N],dg[N],udg[N];//网格数n
int n;void dfs(int u)
{//搜索完毕，并且符合要求时打印if(u==n){for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){cout<<path[i][j];}cout<<endl;}cout<<endl;return;}//y代表y轴上的点for(int y = 0; y < n; y++){//如果一列里面没有元素，对角线上没有元素，那么放入皇后Q;if(!col[y]&&!dg[y+u]&&!udg[y-u+n]){path[u][y]='Q';col[y]=dg[y+u]=udg[y-u+n]=true;//皇后数+1，进入下一层搜索dfs(u+1);//回溯到原始状态col[y]=dg[y+u]=udg[y-u+n]=false;path[u][y]='.';}}}int main()
{cin>>n;//先初始化网格，再由dfs确定皇后位置for(int i = 0; i < n; i++){for(int j = 0; j < n; j++){path[i][j]='.';}}//从第0层开始（初始皇后数为0）dfs(0);return 0;
}

这里解释一下对角线的判定：

由直线方程y=（±）x+b；

我们想要一条对角线上的皇后只有一个，而一条直线上，截距是一样的，b = y ± x ；

但是由于数组的下标没有负数， y - x 有可能是负数，所以加上n，映射成正数！

如果（u）dg[ b ] 为真，那么该直线上已经有一个皇后。

4.2 法2

#include <iostream>
using namespace std;
const int N = 20;
char path[N][N];
//判断行，列，对角线
bool row[N],col[N],dg[N],udg[N];
int n;void dfs(int x,int y,int s)
{//初始化条件if(y == n){x++;y = 0;}if(x == n){//搜素完毕，并且符合要求的条件if(s==n){for(int i = 0; i < n; i++){puts(path[i]);}puts(" ");}return;}//初始化网格path[x][y]='.';dfs(x,y+1,s);//思路同法1if(!row[y]&&!col[x]&&!dg[x+y]&&!udg[y-x+n]){row[y]=col[x]=dg[x+y]=udg[y-x+n]=true;path[x][y]='Q';dfs(x,y+1,s+1);row[y]=col[x]=dg[x+y]=udg[y-x+n]=false;path[x][y]='.';        }}
int main()
{cin>>n;dfs(0,0,0);return 0;
}

但是法2在效率上远不如法1，因为在初始化回溯时进行搜索，浪费了很多不必要的搜索，只有当x，y回溯到0时才真正起到作用。

举此法是为了说明dfs的灵活性。